基于Wardrop第二原理的中轉旅客換乘緊張度優化模型研究

葛慶紅，韓 印 （上海理工大學，上海 200093）

GE Qinghong,HAN Yin (University of Shanghai for Science and Technology,Shanghai 200093,China)

0 引言

當前旅游業的發展帶動著機場客流量的遞增，為適應發展，航空公司需要在機場增設衛星廳，新增的衛星廳有效提升了機場的服務能力，但衛星廳對中轉航班旅客的換乘也帶來了一些問題，同時對登機口的分配提出了新的挑戰。

航班—登機口分配問題是最優化分配包括最小化使用登機口數量、最小化旅客的中轉時間兩個部分，它們之間相互約束，構成一個整體上的運籌學優化問題[1-3]。現有的研究一般采用按階段次序分解成子問題的方式求解[4-6]，陳欣等[7]研究成果表明合理指派停機位可以降低旅客步行距離，提高機場服務水平。Haghani等[8]在最小化旅客航站樓內的步行距離時，綜合考慮了航班之間的轉機旅客數量和停機位之間的距離，更加有效降低旅客步行距離。Yan等[9]針對乘客行走路程與等待時間建立了整數規劃模型，該模型較好地體現了乘客登機前的整個過程。劉君強等[10]研究了實時登機口分配問題，并提出了相關分配算法。

目前為止，研究航班和登機口分配問題和減少乘客步行距離的專家和學者有很多[11-13]，成果頗豐，研究對象通常為同一航站樓，登機口優化分配模型較成熟，但針對中轉乘客換乘的登機口分配模型顯得不足，且現有的模型進行登機口分配時缺乏對中轉乘客換乘時間和中轉乘客前后航班連接時間的考慮。本文以新建衛星廳和航站樓為研究對象，考慮中轉乘客換乘時間和中轉乘客前后航班連接時間兩個主要因素，定義了“換乘緊張度”這一概念，以最小化換乘緊張度為目標對登機口優化分配進行建模，并同時考慮最小化登機口使用數量。

1 優化方法的基本思想

本文采用上海浦東國際機場提供的相關資料。衛星廳和航站樓之間設置有捷運路線相連接，國際國內旅客可以在兩區域之間快速往來，單程需要8分鐘，即h，同一個登機口的兩航班之間的間隔時長不少于45分鐘，即0.75h，且中轉航班對應到達、出發的兩個航班須分配在相同登機口。

1.1 問題分析。中轉航班與登機口的匹配不僅需要考慮到達/出發類型、寬窄機體的匹配，還需考慮到時間的限制，這是一個復雜的問題，為簡化建立模型的難度，本文采用集合分類的思想的基礎上循序漸進的進行匹配建模。

中轉航班的類型眾多，按到達/出發可分為4類，分別用集合pn表示，如表1所示。

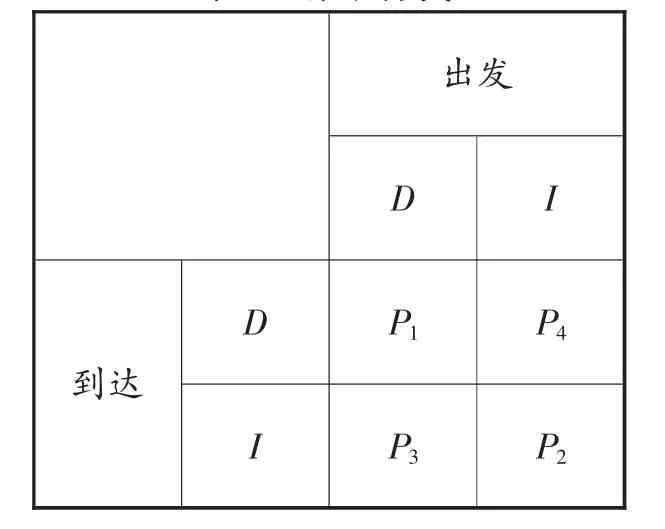
表1 航班分類

登機口（上海浦東國際機場）可分為6類，分別用集合gm表示，如表2所示。

表2 登機口分類

為將簡化問題建模，綜合表1和表2的信息，按到達/出發的規則將登機口和航班進行初步匹配，匹配結果如表3所示。

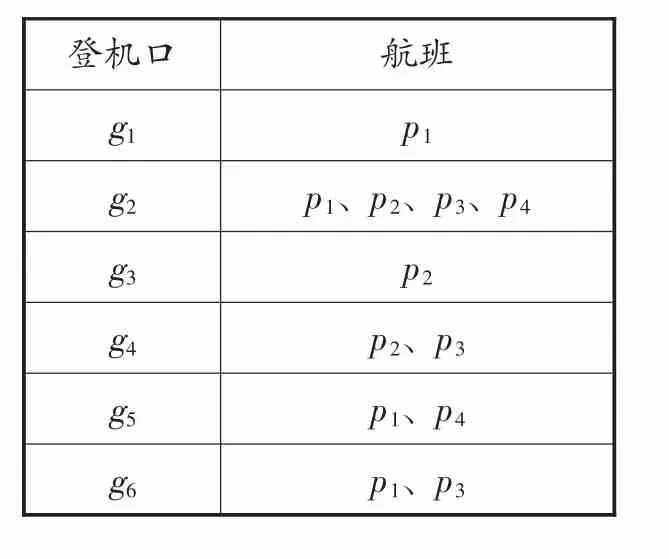
表3 航班—登機口初匹配

1.2 換乘緊張度。首先本文對換乘緊張度的定義如下：

其中：旅客換乘時間=行走時間+最短流程時間+捷運時間；航班連接時間=后一航班出發時間-前一航班到達時間

1.3 Wardrop第二原理的應用。交通規劃領域進行交通分配時，通常采用Wardrop第一、第二原理，Wardrop第一原理從用戶角度考慮，強調用戶平衡；Wardrop第二原理從系統的角度考慮，強調系統最優；其中Wardrop第二原理為：車輛在網絡上的分布，使得網絡上所有車輛的出行時間最小[14]。

本文基于此原理將乘客的到達、出發航班視為一組OD對，中轉乘客的換乘時間即交通阻抗，在登機口布局信息已知的情況下，分配各OD對的登機口進行優化建模，使得所有OD對的換乘緊張度最小即原理中的出行時間最小。

2 模型建立

2.1 目標函數。首先定義兩個0-1變量：

k旅客記錄號的捷運時間如式（1）所示：

式中，sk表示第k個旅客記錄號中的人數；xk表示第k個旅客記錄號的到達航班號；yk表示第k個旅客記錄號的出發航班號表示集合g中jm登機口到集合中登機口的捷運次數，其數值在表1中可以查到。表示嚴格約束到達航班和出發航班必須與旅客記錄號中的航班信息是一一對應，否則該值為

k旅客記錄號的行走時間如式（2）所示。

k旅客記錄號的最短流程時間如式（3）所示。表示乘客從集合gm中j登機口到集合

式中，lyk表示k旅客記錄號中出發航班的時刻；lxk表示k旅客記錄號中到達航班的時刻。k旅客記錄號的換乘緊張度如式（5）所示。

第一個目標函數為所有的中轉旅客記錄號中的旅客換乘緊張度最小，即如式（6）所示。

在減少乘客緊張度的同時，需要同時兼顧機場的運營成本，即盡量減少登機口的使用數。

定義如下0-1變量。第二個目標函數即最小化登機口的使用數量，如式（7）所示。

2.2 約束條件。首先針對機型定義兩個0-1變量。

約束中相關參數的取值如下：

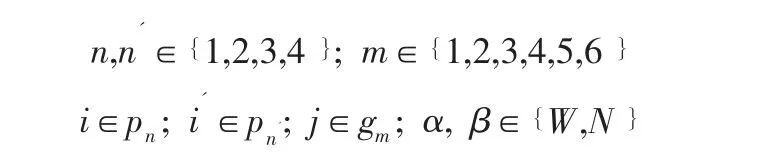
所述的機型約束即到達航班的機型與其分配的登機口機型嚴格一致，如式（8）所示。

所述的同一登機口的兩航班之間的空擋間隔時間必須大于等于0.75h（45min），如式（9）、（10）、（11）所示。

從到達/出發類型角度出發，約束有：g1中的登機口只對P1中的航班服務，如式（12）所示。

g3中的登機口只對P2中的航班服務，如式（13）所示。

g4中的登機口

只對P2、P3中的航班服務，如式（14）所示。

g5中的登機口只對P1、P4中的航班服務，如式（15）所示。

g6中的登機口只對P1、P3中的航班服務，如式（16）所示。

每一個轉場飛機號中的航班最多分配一個登機口，如式（17）所示。

3 模型分析

以往模型多強調登機口的優化分配，來減少機場的運營成本，對以中轉旅客為對象的登機口分配優化模型研究目前尚未檢索到。本文建立的雙目標優化模型相對傳統的登機口優化分配模型具有以下特點：（1）以往登機口分配模型較少考慮到乘客出行的換乘行為，本模型考慮出行換乘行為，優化目標為雙目標，分別為換乘緊張度和登機口使用數量，可以中轉旅客換乘緊張度最小為目標進行第一次求解，在求解結果的基礎上以登機口使用數量最少為目標進行第二次求解，從而達到最小化中轉旅客換乘緊張度的同時優化登機口使用數量。（2）模型在建立的過程中充分考慮到了信息交互，同時優化中轉旅客前后航班的登機口分配，來減小中轉乘客的換乘緊張度。（3）模型優化方法的思想是Wardrop第二原理，基于Wardrop第二原理對問題進行分析與數學建模，理論支撐更加成熟。（4）本文的優化模型以新建衛星廳機場為研究對象，選用登機口匹配準則等作為約束，在現實中將具有較好的實用價值。

4 結論

本文基于Wardrop第二原理對新增衛星廳機場中的中轉旅客換乘緊張度進行了優化研究，將乘客的到達和出發航班視為一組OD對，在航班—登機口的匹配規則基礎上考慮信息交互，以換乘緊張度、登機口使用數量為目標和航班—登機口匹配規則為約束建立了雙目標優化模型，從而在優化中轉乘客換乘緊張度的同時盡量減少了登機口的數量。未來在數據允許的條件下，學者可以針對中轉旅客利用該模型對實際生活中的航班衛星廳登機口分配進行實例分析。