2014年高考福建卷文科第12題的源與流

福建省龍巖市長(zhǎng)汀縣第二中學(xué) (366300)

邱有文

2014年高考福建卷文科第12題是一道以新定義題型的創(chuàng)新題.該題以橢圓的定義為載體，探究在新情境下“橢圓”生成的基本步驟和圖形特征，重現(xiàn)“軌跡”的基本研究方法，注重考查了考生抽象概括能力、對(duì)數(shù)學(xué)概念的理解、數(shù)學(xué)思想方法的掌握、探索與創(chuàng)新的水平以及應(yīng)用數(shù)學(xué)解決實(shí)際問(wèn)題的能力等.

1.試題展示

(2014年高考福建卷文科第12題)在平面直角坐標(biāo)系中，兩點(diǎn)P1(x1,y1)，P2(x2,y2)間的“L-距離”定義為‖P1P2|=|x1-x2|+|y1-y2|.則平面內(nèi)與x軸上兩個(gè)不同的定點(diǎn)F1，F(xiàn)2的“L-距離”之和等于定值(大于‖F(xiàn)1F2|)的點(diǎn)的軌跡可以是( ).

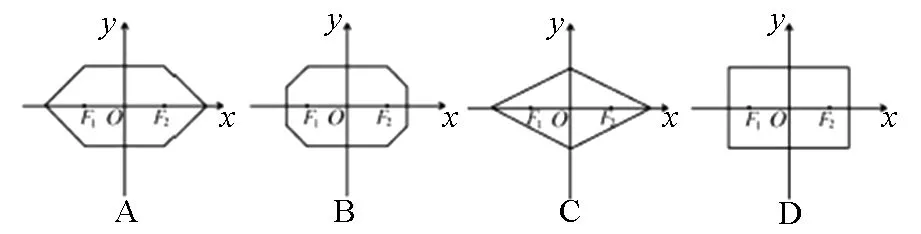
2.試題解答

解析:根據(jù)題意,不妨設(shè)F1(-1,0)，F(xiàn)2(1,0)，由“L-距離”定義可得|x+1|+|y|+|x-1|+

|y|=2a，且2a>|F1F2|，即a>1.

當(dāng)x≥1,y≥0時(shí)，x+y=a；當(dāng)x≥1,y<0時(shí)，x-y=a；當(dāng)-1

-1

由上述六種情況的討論，可以作出點(diǎn)P的軌跡為六邊形，即選A.

3.試題題源

題源1(2010年高考廣東卷第21題)設(shè)A(x1,y1)，B(x2,y2)是平面直角坐標(biāo)系xOy上的兩點(diǎn)，現(xiàn)定義由點(diǎn)A到點(diǎn)B的一種折線(xiàn)距離ρ(A,B)為ρ(A,B)=|x2-x1|+|y2-y1|，對(duì)于平面xOy上給定的不同兩點(diǎn)A(x1,y1)，B(x2,y2).

(1)若點(diǎn)C(x,y)是平面xOy上的點(diǎn)，試證明ρ(A,C)+ρ(C,B)≥ρ(A,B)；

(2)在平面xOy上是否存在點(diǎn)C(x,y)，同時(shí)滿(mǎn)足

①ρ(A,C)+ρ(C,B)=ρ(A,B)②ρ(A,C)=ρ(C,B).若存在，請(qǐng)求出所有符合條件的點(diǎn)，請(qǐng)予以證明.(解答參考2010年廣東高考試題)

題源2 (某地市高三月考試題)在平面直角坐標(biāo)系中，定義d(P,Q)=|x1-x2|+|y1-y2|為兩點(diǎn)P(x1,y1)，Q(x2,y2)之間的“折線(xiàn)距離”.在這個(gè)定義下，給出下列命題:

①到原點(diǎn)的“折線(xiàn)距離”等于1的點(diǎn)的集合是一個(gè)正方形；

②到原點(diǎn)的“折線(xiàn)距離”等于1的點(diǎn)的集合是一個(gè)圓；

③到M(-1,0),N(1,0)兩點(diǎn)的“折線(xiàn)距離”之和為4的點(diǎn)的集合是面積為6的六邊形；

④到M(-1,0),N(1,0)兩點(diǎn)的“折線(xiàn)距離”差的絕對(duì)值為1的點(diǎn)的集合是兩條平行線(xiàn).

其中正確的命題是.(寫(xiě)出所有正確命題的序號(hào))

至此，2014年福建省高考文科第12題源頭就浮出了水面.

4.試題變式

在平面直角坐標(biāo)系xOy中，O為坐標(biāo)原點(diǎn).定義P(x1,y1)、Q(x2,y2)兩點(diǎn)之間的“L-距離”為d(P,Q)=|x1-x2|+|y1-y2|.

①已知B(1,0)，直線(xiàn)x-y+2=0上的動(dòng)點(diǎn)M，則d(B,M)的最小值為;

③已知點(diǎn)A(1,3)，B(3,6)，M(x,y)，且x∈[0,6],y∈[0,9]，若d(A,M)=d(B,M),則M的軌跡的長(zhǎng)度為.

5.試題推廣

對(duì)上述試題的變式可以進(jìn)行推廣：

在平面直角坐標(biāo)系xOy中，O為坐標(biāo)原點(diǎn).定義P(x1,y1)、Q(x2,y2)兩點(diǎn)之間的“L-距離”為d(P,Q)=|x1-x2|+|y1-y2|，則有下面結(jié)論：

對(duì)于上述結(jié)論1、結(jié)論2、結(jié)論3的證明略.