由一道三角題的多解談“一題多解”

江西省井岡山經貿學校 (331600)

肖 武

1.引言

我們知道，一題多解可以更好地鞏固學生知識，訓練學生思維，開拓學生視野.通過多角度審視一道題，達到強化學生思維的連貫性，知識的銜接性，由此，培養學生充分地利用所學知識解決數學問題.本文例舉一道三角題的一題多解予以說明.

2.題目

圖1

如圖1，在△ABC中，

3.多解

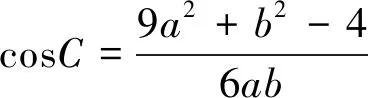
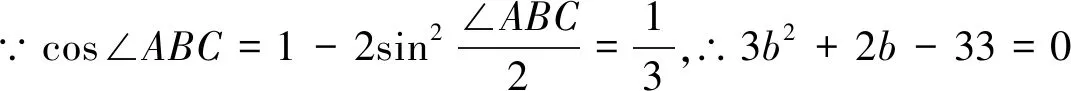
評注：解法中充分運用題目條件，由余弦定理構造等式尋求三角形的邊角關系，這是三角問題的一般求法.

評注：解法中靈活運用了正余弦定理及三角函數邊角關系求解.

評注:利用向量關系求解三角問題也是一般通法.

圖2

評注:解法中的輔助線具有事半功倍之效.

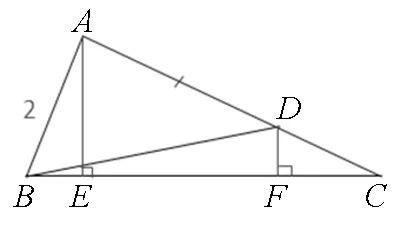
圖3

評注：求解中巧妙地運用條件AD=2DC,使問題簡單化.

4.結語

以上一道三角題的解題實踐中，既用了三角知識，又用了向量知識，還用到了作輔助線的手段，達到解題方法多元化.所以在解題教學過程中，我們應強調通過一題多解的探索，融合學生多方面數學知識，拓寬學生的解題思路，引導學生在解題實踐中去領悟，從而真正實現發展學生的數學核心素養.