關注課堂生成，促進思維發展

中國農業大學附屬中學 蔡明艷

錢學森教授曾指出：“教育工作的最終機智在于人腦的思維過程。”人類的活動離不開思維，思維活動的研究是教學研究的基礎，數學教學就是指數學思維活動的教學，就是學生在教師的指導下，通過數學思維活動，學習數學家思維活動的成果，并發展數學思維。數學思維能力是數學能力的核心，要培養學生的數學思維能力，就要在教學中展現思維過程，讓學生親自參與思維活動，而課堂問題的動態生成可以很好地體現學生的思維活動。

在數學教學中,生成性教學就是指在教學目標的設預下,在師生交往互動中,以即時出現的有價值、有創見的數學問題或數學情境為契機,挖掘學生的潛能,引發學生深入思考,師生之間、學生之間交往互動與共同發展。本文圍繞《與平行線有關的角的計算》這一節課，就如何在初中數學教學中體現動態生成談談自己的做法。

一、感知幾何問題的生成過程，體會還原定理圖形的思想

數學教學要研究知識的起源，在此基礎上引導學生感受問題是怎樣一步一步形成的，在形成的過程中關注派生出來的問題，并確立研究問題的方向。例如，在本節課提出初始性問題：

【問題1】已知直線AB∥CD，那么我們是如何研究平行線的呢？引導學生理解問題的根源，并在此基礎上通過添加圖形元素，讓學生發現問題并提出問題，不斷形成新的挑戰性問題，激發學生的探究欲望。

【問題2】若再增加一條截線GH，又會有產生哪些數學問題呢？

添加第二條截線GH時，需要考慮它與第一條截線MN的位置關系，滲透研究幾何問題的方法，即首先關注圖形之間的位置關系。

第一種情況：GH與MN平行。此時引導學生感知當引入第二條截線時，又會產生一些角，相鄰2個點之間的角的關系我們已經探究完了，那么不相鄰的交點處的角是否存在數量關系呢？在學生敘述角關系的過程中，進一步體會平行線具有轉移角的作用。

第二種情況：GH與MN相交。此時學生會發現若GH與MN相交于點P，則點P對于原有圖形平行線會有哪些可能的位置呢？學生在畫圖與幾何畫板的動態演示過程中發現點P可能在其中一條平行線上；點P可能在兩條平行線之間；點P可能在兩條平行線外。在這個過程中引導學生體會幾何問題的形成過程，學生自己發現研究方向，并滲透分類思想。

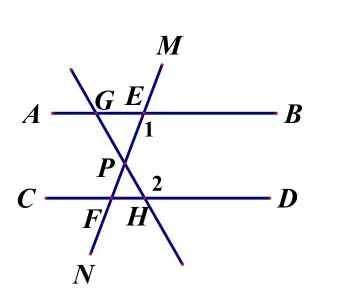
圖1

【問題3】以點P在平行線內為例，如圖1，我們已經知道∠1、∠2分別決定了兩條截線的方向，但兩條截線又形成了一個角，即∠EPH，那么兩條截線的夾角∠EPH與∠1、∠2是否存在一定的聯系呢？

這個過程是通過在基本圖形的基礎上添加圖形元素，形成新的數學問題，體會幾何問題的形成過程，分類思想是學生自己發現的，學生的問題意識、空間觀念和幾何直觀等學科素養在對話過程中自然而然地得到培養和提升。

而學生在解決問題時發現，這3個角之間位置不相關，需要建立它們之間的聯系。怎么建立聯系呢？學生在交流探究中得到不同的輔助線的作法，并歸納它們的共性，發現最終是還原了定理圖形，借助平行線建立了不同位置的角之間的關系，并得出結論：∠1+∠P+∠2=360°。

二、動態生成幾何問題，展示思維的有序性

用動態觀點看待幾何問題，有助于建立學生思維的有序性，滲透由一般到特殊，再由特殊到一般的研究方法，使學生在面對新的問題時能夠找到解決問題的一般方法，揭示問題形成的本質。

【問題4】若點P在其他的位置，情況又如何呢？

此時，我們可以借助幾何畫板動態演示，當點P在直線AB上，剛才的結論還成立嗎？幾何畫板的動態演示讓點P順時針轉動一圈，在圖形的變化過程中學生發現，當點P與平行線的位置發生變化時，其形成的角的數量關系也在發生變化，這就是說，圖形的數量關系是由位置關系所決定的。通過圖形運動，建立從動態視角認識幾何問題形成的過程，在圖形運動過程中把握圖形的不變關系，體會圖形位置與數量之間的內在聯系。同時，滲透從簡單到復雜的研究方法以及分類思想，培養學生的幾何思維能力。

三、滲透數學思想方法，體會問題生成的本質

數學思想方法是教學的本質，課堂教學要通過對變式問題的研究，培養學生探究問題根源的意識，正所謂“求根索源”，把握問題的實質.

【問題5】如果增加第3條截線，又會形成哪些圖形呢？角之間又會存在怎樣的數量關系呢？

【問題6】若平行線AB、CD之間有n個點P1，P2，P3，…，Pn，形成∠1，∠2，…，那么這些角之間又存在怎樣的數量關系呢？

由于點P的位置不同，所以會形成不同位置的圖形，引導學生進一步體會圖形位置對數量關系的影響，通過增加截線的條數，體會圖形變化過程中不變的圖形關系，增強學生的研究意識，激發學生的探究欲望，進一步體會轉化思想在研究幾何問題中的作用。

本節課以讓學生進行獨立思考、共同探索、驗證猜想為主線的課堂形式組織教學，給了學生更多展示自己的機會，讓學生在充分思考的同時，找出思維漏洞，使他們在自我認識、自我完善的基礎上學會從不同角度考慮問題，學會如何思考的過程。

我們教師應該把上好每一節課看成是對生命構成的高度珍惜，帶著以學生終身發展為本的新理念，以培養學生數學核心素養為目標，在每一節課的教學設計中幫助學生學會思考。教師對課堂上生成性因素的巧妙把握，提升了課堂教學的價值，使得我們的課堂充滿活力，充滿數學味道，讓學生的思維得以真正發展。