如何提升高中學生解析幾何的學習能力
福建省武夷山第一中學 葛香珠
在高中一線教學二十幾年發(fā)現,教師教一個知識點,只要十幾分鐘或者幾十分鐘,但卻往往要花上幾倍的時間來批改學生的作業(yè)本,而作業(yè)中出現的許多錯誤即使是剛剛在課堂上集體分析過、提醒過、提問過、總結過,可還是有好一部分學生過后又再次出錯!究其原因,是有些同學流于形式,并沒有真正消化題目,特別是高中解析幾何題目,如果不能從平常作業(yè)中培養(yǎng)起學生的直觀想象能力,從解題中吸取“營養(yǎng)”,將很難培養(yǎng)學生分析問題、解決問題的能力,提升學生的核心素養(yǎng)。
直觀想象是分析和解決數學問題的重要手段,是解析幾何中進行邏輯推理、構建抽象結構的思維基礎。在直觀想象核心素養(yǎng)的形成過程中,能增強學生運用圖形和空間想象能力、數形結合的能力,從本質上提升學生的學習能力,可以嘗試從以下幾方面入手:
一、讀題
學會讀題,了解題目內容,是培養(yǎng)學生審題能力的開始。認真讀題,透徹掌握題意,通過再次認真讀題,溫故而知新,往往就能知道自己原來怎么就錯了,并形成正確的讀題、解題習慣。教師應培養(yǎng)學生反復、仔細、邊讀邊想、邊標記重點的讀題習慣。
如例1,教師可以示范讀題方法及注意事項,學生演練,從而培養(yǎng)學生的讀題能力,提高學生的閱讀能力。
二、背題
對于數學成績不太理想的學生,或學習高中數學有困難的學生,有的甚至都想放棄學數學的學生,常常是想獨立完成解析幾何試題基本都是不可能的。這時可建議他們通過“背數學題”的學習方法,達到有效解題、訂正試題的目的,這個技巧是不會做或做錯了卻又很難理解哪里錯的問題,直接看解答,先背起來再說。那如何背,怎么背呢?
1.背定義、背公式
高中圓錐曲線的定義及幾何性質應用靈活,幾何直觀圖形與代數公式的關系,新授課時很多同學認為很難,主要原因是公式多,圖形性質多,因此,將重要的數學概念、公式、幾何性質等背起來是一種行之有效的方法。
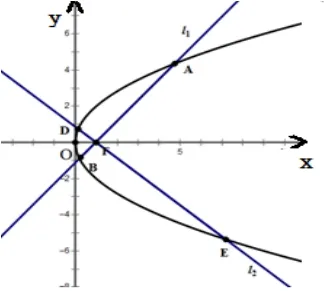
A.16 B.14 C.12 D.10
由公式得(如上述所背公式②):
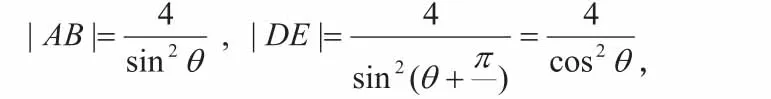
可見,通過熟背公式也能達到快速、正確解答解析幾何試題的目的。
2.背圖形
新學的圖形先背起來再說,能默寫下來更好,最后再考慮如何作圖則更完美。如此一來,一個圖形一般只要幾分鐘便背下來,從量上來看,可能追趕得上成績好的同學,遇到相同題型不僅能達到解題的目的,還能減少錯誤的發(fā)生。
從近幾年高考數學或全國高中數學聯賽試題中的解析幾何試題看,先學會畫圖,才知道相對關系,對學生的直觀想象能力要求也在不斷提高,數形結合是解析幾何的重要思想方法,因此我們平時教學時,能畫圖的盡量畫出圖形,讓學生觀察到老師如何使用尺規(guī)作圖,最好是學生也作圖,以利于正確地理解題意、快速地解決解析幾何問題。
為了學生能更好地訂正及掌握圖形,雖然教學基本功扎實的教師可以徒手畫出漂亮的圖形,但是徒手畫圖顯而易見的缺點是學生缺失了觀察教師使用工具畫圖的過程和感悟,少了邊學邊模仿教師徒手畫圖的經驗。對幾何學習來說,畫圖與識圖是基本功,所以畫圖活動要滲透每一節(jié)數學課。
三、寫題
在平時的新課學習中,要養(yǎng)成習慣,把課本、練習、試卷上的好題或做錯的錯題認認真真地做好標記,不會做的也做好標記,按模塊訂正在固定的、專用的好題本和錯題本上。高三一輪復習,特別是溫書假時,再把好題、錯題或原先不會做的題(選做)再做一遍,通過這種記題(寫題)方式,系統(tǒng)強化所學知識。
該題中,直線與圓錐曲線相交,有涉及中點時,可考慮用點差法,能快速地求出直線的斜率,這個過程中容易忽視直線與圓錐曲線聯立后所得方程為一元二次方程根的判別式的判斷。
對于這類課本上的解析幾何習題,往往是編教材的老師費盡心思、反復考慮才挑選出來,是最具代表性、權威性的試題。一般來講,課本上的習題尤其要注意與概念、公式、定律的聯系,而試題做錯的同學的一大原因就是基礎不牢,為此,很有必要將課本上的試題進行分類梳理。課本上的習題,有的老師講過,有的教參書上有比較詳細的講解,有的一題多解,做好這類題目是增強學生的學習信心,也是培養(yǎng)他們獨立分析與思考能力素養(yǎng)的一種最有效手段。
四、看題
在距高考的最后一個月里,應建議一個“看”字,多看課本上,習題中分類整理出來的試題,思考相同類型試題之間的聯系與差別。學生真正掌握知識應該有個過程,所以對于學過、做過的試題,要經常回過頭來看看,并做好分類標志。
正如日本學者和田秀樹頗有感觸地說:“數學好不好,其實與學習方法有關。”針對高中生解析幾何學習能力的培養(yǎng)問題,如果能從培養(yǎng)學生的讀題、背題、寫題及看題能力幾個方面入手,加強學生核心素養(yǎng)形成,提升學生直觀想象能力,無疑是培養(yǎng)高中生學習能力的一種有效途徑。

