基于雙層隔振的船用空壓機系統(tǒng)振動建模研究

金麗瓊，邢志勝，朱寶慶，崔冬，李國強

(合肥通用機械研究院有限公司，安徽 合肥 230031)

空氣壓縮機(以下簡稱空壓機)是現(xiàn)代船舶工業(yè)中的重要關(guān)鍵設(shè)備之一，目前船用空壓機多采用往復(fù)活塞式，由于不平衡慣性力等因素的影響，往復(fù)活塞式空壓機在工作時會產(chǎn)生振動和噪聲，影響船舶的隱身性和舒適性，同時，復(fù)雜的海況等因素會通過船體反作用于空壓機，使空壓機的工作環(huán)境更加惡劣，很容易造成空壓機的損壞。

針對前述問題，通常在船用空壓機和甲板之間設(shè)計有單層隔振裝置或雙層隔振裝置(包括浮筏隔振裝置)，隔振裝置一方面能最大限度地隔離空壓機的振動沿機座向船體的傳遞，從而抑制船艙工作室噪聲和水下輻射噪聲，以達(dá)到提高船舶隱身性和舒適性的功能；一方面能有效地抑制外界干擾(如惡劣海況等)通過機座對船舶空壓機設(shè)備的沖擊，以提高空壓機的使用壽命。因此，針對隔振結(jié)構(gòu)的船用空壓機系統(tǒng)動力學(xué)行為的研究受到了廣泛的關(guān)注。俞微等以船用浮筏隔振系統(tǒng)為研究對象，實例驗證了多層隔振系統(tǒng)的穩(wěn)定性計算方法及通用程序。魯克明等建立了某艇用空壓機雙層隔振系統(tǒng)模型，并對其進(jìn)行了參數(shù)及結(jié)構(gòu)優(yōu)化分析。杜奎等運用導(dǎo)納原理推導(dǎo)了雙層減振裝置隔振器對齊安裝和不對齊安裝方案的傳遞功率流，發(fā)現(xiàn)由于結(jié)構(gòu)傳遞導(dǎo)納小于輸入導(dǎo)納，不對齊安裝更有利于降低寬頻率振動的傳遞。祝華等采用試驗方法研究了隔振器安裝位置的偏差對隔振效果的影響，發(fā)現(xiàn)隔振器安裝位置偏差的變化可以明顯影響高頻段的隔振效果。尚國清、馬永濤等結(jié)合艦船設(shè)備的減振降噪研究，就浮筏系統(tǒng)的動力學(xué)建模分析展開了深入的討論，全面分析了浮筏系統(tǒng)的多剛體動力學(xué)建模法、有限元法、阻抗綜合法、模態(tài)阻抗法綜合法等建模方法，闡述了各種建模方法的特點。

本文在上述研究的基礎(chǔ)上，結(jié)合工程應(yīng)用，以基于雙層隔振結(jié)構(gòu)的船用空壓機為研究對象，將空壓機和隔振塊簡化為剛體，中間的減振塊簡化為彈簧阻尼系統(tǒng)進(jìn)行研究，采用Newton 法建立了基于雙層隔振的船用空壓機系統(tǒng)振動模型，為船用空壓機系統(tǒng)的動態(tài)特性分析、優(yōu)化設(shè)計以及振動控制等方面提供了較為可靠的工具和理論依據(jù)。

1 基于雙層隔振結(jié)構(gòu)的船用空壓機振動模型

雙層結(jié)構(gòu)的船用空壓機動力系統(tǒng)主要由船用空壓機、減振塊、中間質(zhì)量塊等部分組成，如圖1。在雙層隔振結(jié)構(gòu)的船用空壓機系統(tǒng)中，為保證空壓機的正常運行，空壓機和中間質(zhì)量塊通常都具有較高的強度和剛度，且相對于其結(jié)構(gòu)尺寸來說，空壓機和中間質(zhì)量塊在振動過程中的自身變形較小，因此，在雙層隔振結(jié)構(gòu)的空壓機系統(tǒng)中，可將空壓機和中間質(zhì)量塊視為剛體來對待。考慮到發(fā)生振動時空壓機與中間質(zhì)量塊、中間質(zhì)量塊與船體之間相對位移非常小，建模時可將空壓機與中間質(zhì)量塊中間質(zhì)量塊與船體之間的減振塊視為線性彈簧阻尼系統(tǒng)，如圖2。空壓機與中間質(zhì)量塊之間安裝4個減振塊，中間質(zhì)量塊與船體之間安裝有6 個減振塊。

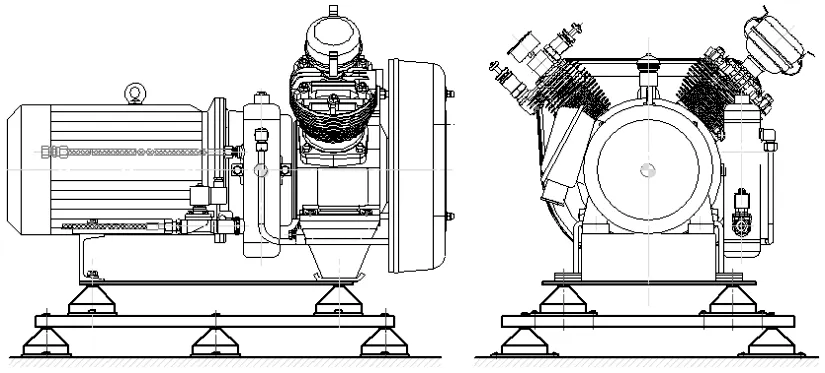
圖1 某型船用空壓機

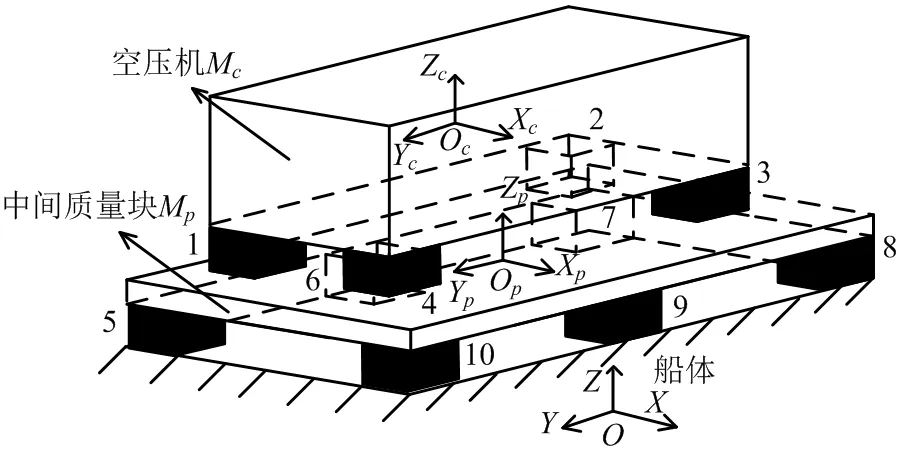
圖2 隔振結(jié)構(gòu)的空壓機振動模型

在圖2 中，OXYZ 是位于船體的絕對坐標(biāo)系，OcXcYcZc是以空壓機質(zhì)心Oc為原點的相對坐標(biāo)系，OpXpYpZp是以中間質(zhì)量塊質(zhì)心Op為原點的相對坐標(biāo)系。模型中主要包括空壓機、減振塊、中間質(zhì)量塊以及船體，其中0 處代表空壓機往復(fù)慣性力等因素的激勵位置，1 ～4 處代表空壓機與中間質(zhì)量塊連接位置，5 ～10 處代表中間質(zhì)量塊與船體連接位置。本文考慮的基于隔振結(jié)構(gòu)的空壓機系統(tǒng)振動模型共有12 個自由度，即將空壓機和中間質(zhì)量塊視為2 個具有6 自由度的空間剛體結(jié)構(gòu)(3 個平動和3 個轉(zhuǎn)動)。設(shè)空壓機的質(zhì)量為mc，空壓機繞坐標(biāo)軸Xc、Yc和Zc的轉(zhuǎn)動慣量分別為Jcx、Jcy和Jcz，空壓機激勵源位置以及空壓機與減振塊連接位置各點的受力可表示為各受力點在坐標(biāo)系OcXcYcZc中的位置坐標(biāo)可表示為lic=(lxic,lyic,lzic)T(i=0,1,···,4)，當(dāng)受力點位置位于坐標(biāo)軸正向時，其坐標(biāo)值取正值，當(dāng)受力點位置位于坐標(biāo)軸負(fù)向時，其坐標(biāo)值取負(fù)值；設(shè)中間質(zhì)量塊的質(zhì)量為mp，中間質(zhì)量塊繞坐標(biāo)軸Xp、Yp和Zp的轉(zhuǎn)動慣量分別為Jpx、Jpy和Jpz，中間質(zhì)量塊上各作用點的受力可表示為Fip=(Fxip,Fyip,Fzip)T，各受力點在坐標(biāo)系OpXpYpZp中的位置坐標(biāo)可表示為lip=(lxip,lyip,lzip)T(i=1,2,···,10)，當(dāng)受力點位置位于坐標(biāo)軸正向時，其坐標(biāo)值取正值，當(dāng)受力點位置位于坐標(biāo)軸負(fù)向時，其坐標(biāo)值取負(fù)值。點1 ～4 處減振塊的剛度和阻尼矩陣均可分別表示為kic=diag(kxic,kyic,kzic)和cic=diag(cxic,cyic,czic)； 點5 ～10 處 減 振 塊 的 剛 度和阻尼矩陣均可分別表示為kip=diag(kxip,kyip,kzip) 和以系統(tǒng)的靜平衡位置作為初始狀態(tài)假設(shè)中間質(zhì)量塊在外力Fip的作用下發(fā)生的位置變化可表示為Xp=(xp,yp,zp,θpx,θpy,θpz)T，則可推導(dǎo)出中間質(zhì)量塊的6 自由度振動微分方程的矩陣表達(dá)式

式（1）中減振塊耦合點處作用力的力矩正負(fù)號是由于作用力和耦合點處的坐標(biāo)來共同確定的。式（1）可用矩陣形式表示如下：

并且有

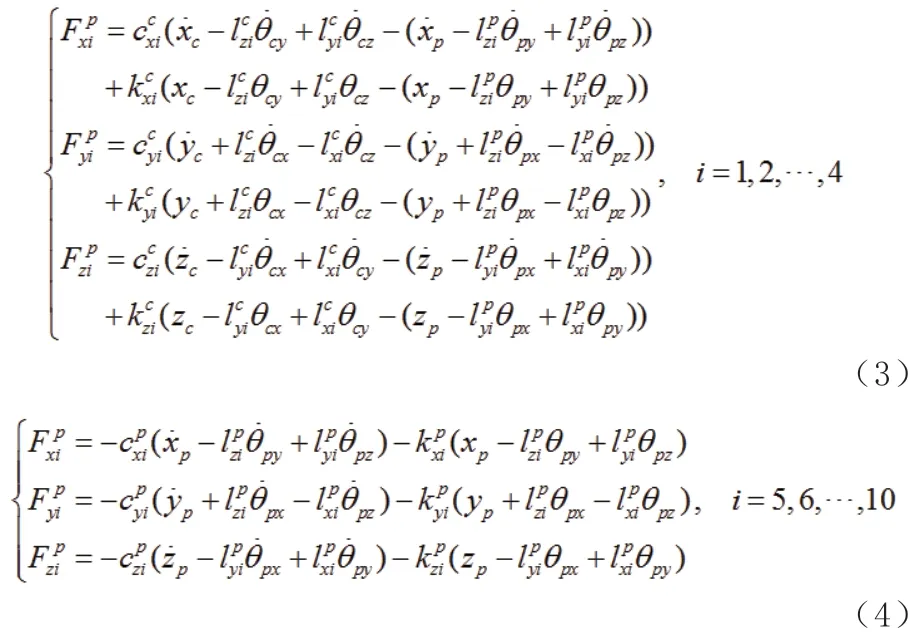
將式(3)和式(4)寫成矩陣形式得

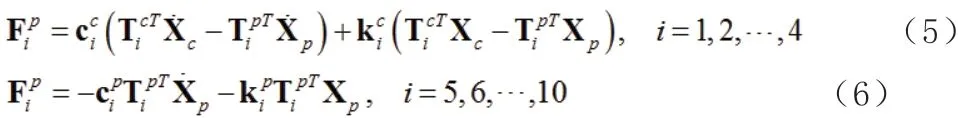
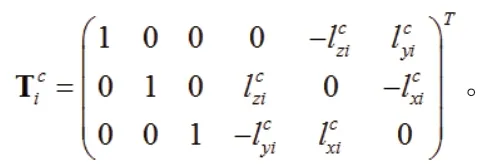
將式(2)和式(7)合并可寫為：

將式(5)和式(6)代入式(8)，并整理得

式中各元素表達(dá)式為：

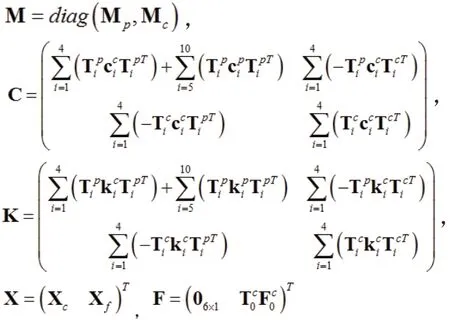
2 模型有效性分析

方程（9）的結(jié)構(gòu)形式與嚴(yán)濟寬等在文獻(xiàn)[14]和周世雄等在文獻(xiàn)[15]中提出的雙層隔振模型相似。在該模型（9）的基礎(chǔ)上，如果僅考慮空壓機和中間質(zhì)量塊在垂直方向上的兩個自由度，則模型（10）可簡化為：

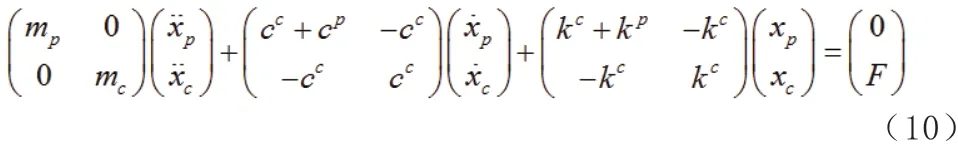
此時，得到的空壓機系統(tǒng)振動模型與文獻(xiàn)[9]和[16]曾經(jīng)提出的船用空壓機系統(tǒng)振動模型是一致的；如果模型（10）中僅考慮單層隔振的作用，忽略中間質(zhì)量塊和減振塊阻尼特性的影響，且僅考慮空壓機系統(tǒng)的自由振動，則模型（10）可簡化為：

式中各元素表達(dá)式為：

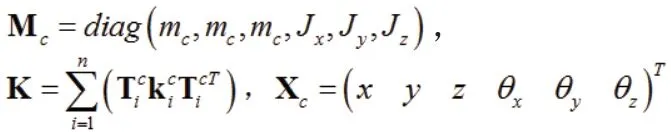
其中剛度矩陣K 中的n 代表空壓機與船體之間減振塊的數(shù)量。此時，得到的空壓機系統(tǒng)振動模型與文獻(xiàn)[3]描述船用空壓機6 自由度剛體模型一致的；由此可以看出，本文提出的基于雙層隔振系統(tǒng)的空壓機振動模型在設(shè)定條件下可以推導(dǎo)出上述文獻(xiàn)中的研究模型，因此本文提出的振動模型具有較強的適用性和通用性。

3 結(jié)語

（1）考慮空壓機和中間質(zhì)量塊的耦合作用，將雙層隔振結(jié)構(gòu)的空壓機振動系統(tǒng)簡化為12 個自由度，使整個模型可以考慮的因素更多，更接近實際情況，模型的通用性更強。

（2）與以往的有效模型進(jìn)行了比較，比較結(jié)果表明本文提出的12 自由度模型考慮的因素更多，形式更通用。

（3）在對船用空壓機振動特性進(jìn)行分析時，不僅要建立其數(shù)學(xué)模型，還需要考慮空壓機不平衡慣性力等因素的影響，同時還要考慮海況等復(fù)雜外部因素的影響，本文僅對雙層隔振結(jié)構(gòu)的船用空壓機系統(tǒng)的數(shù)學(xué)模型進(jìn)行了研究和分析，而對空壓機不平衡慣性力以及海況等復(fù)雜因素對整個系統(tǒng)的動態(tài)響應(yīng)分析將在后續(xù)工作中進(jìn)行完善，從而實現(xiàn)對船用空壓機系統(tǒng)動力學(xué)的完整分析。