云模式下制造服務評價指標的集成賦權方法*

謝 燦，高新勤，王雪萍，席海洋

(1.西安理工大學 機械與精密儀器工程學院，西安 710048；2.西安交通大學 經濟與金融學院，西安 710061)

0 引言

云制造是一種面向服務的制造新模式[1]。在云模式下，制造服務提供方通過制造服務運營方的云制造服務平臺，向制造服務需求方提供各類制造服務，從而實現“分散資源集中使用，集中資源分散服務”[2]。

目前，針對云制造服務組合評價與優選問題，常見的方法是通過指標賦權將多目標模型轉化為單目標模型進行求解。陳浩等將熵值法和層次分析法(AHP)相結合用于指標賦權，避免了單一評價方法的片面性[3]。陳友玲等采用偏好舵法和變精度粗糙集理論計算評價指標的主客觀權重，將綜合求得的效率值作為評價依據[4]。Kumar and Singal采用AHP法、理想解相似度排序法(TOPSIS)和改進的TOPSIS方法選擇最佳的材料[5]。Sadigha等提出使用模糊AHP-TOPSIS算法對合作伙伴進行評估，從而確定每個任務的獲勝企業[6]。通過指標賦權將云制造服務組合多目標優化問題轉化為單目標問題可以獲得最優解，但指標賦權的主、客觀方法很多，如何集成兩種主、客觀賦權方法并發揮各自優勢需要做進一步研究。

本文將G1-法和變精度粗糙集理論分別用于云模式下制造服務評價指標的主、客觀賦權，同時引入基于最大熵原理的組合系數模型，集成主、客觀賦權結果對云制造服務評價的影響，解決傳統綜合賦權法因依賴主觀而可靠性不高以及未能發揮主、客觀兩種賦權方法作用的問題。

1 云模式下制造服務的評價指標

1.1 云制造服務配置過程

在云模式下，制造任務的粒度通常較大，需要由多個制造服務提供者共同完成。云制造服務配置就是按照一定的服務要求和邏輯關系，實現制造服務的供需匹配。具體配置過程包括任務分解、可行服務集獲取以及服務優選等3個階段[7]。

(1)任務分解。將粒度較大的云制造任務分解為多個粒度適中且可被單一制造服務提供者完成的子任務。

(2)可行服務集獲取。從云制造服務平臺中獲取滿足各個子任務需求的可行服務集。

(3)服務優選。從各個可行服務集中優選云服務，形成組合服務，共同完成大粒度的制造任務。

1.2 云制造服務評價指標

影響云制造服務評價的因素很多，通常采用的評價指標有時間、成本、質量、可靠性、提供商經營狀況以及服務評分等。

(1)服務時間T，指云制造服務從被使用到被釋放回到云平臺所消耗的時間。

(2)服務成本C，指服務需求方獲取云制造服務支付的費用。

(3)服務質量Q，指云制造服務能夠滿足服務需求方的程度，通常由服務需求方參考云平臺提供的服務質量評估標準而獲得。

(4)服務可靠性R，指云服務在服務需求方限定時間內完成服務次數與服務總次數的比值。

(5)服務提供方經營狀況S，指服務提供方的經營能力，通常以其在云平臺上單項服務的年營業收入為衡量標準。

(6)服務評分E，指服務需求方對服務提供方相關服務的綜合評價，通過歷史交易數據獲取。

1.3 服務評價指標規范化

由于計量單位和評價準則不同，云制造服務的各指標存在較大差異，需要進行規范化處理[8]。

服務質量Q、可靠性R和評分E為正向指標，越大越好，以服務質量Q為例，歸一化公式為：

(1)

服務成本C屬于負向指標，越小越好，其歸一化公式為：

(2)

服務時間T和服務提供商經營狀況S屬于區間型指標，以服務時間T為例，其歸一化公式為：

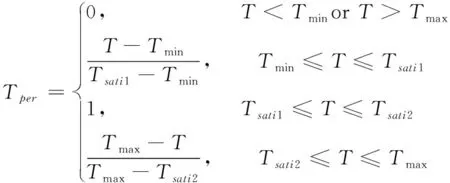
(3)

式中，Tmax和Tmin為可接受的最大、最小交貨時間，[Tsati1,Tsati2為服務需求方滿意的交貨時間區間。

2 云服務評價指標的集成賦權方法

為了兼顧主觀偏好和客觀真實，本文提出基于最大熵原理的集成賦權方法。首先將G1-法和變精度粗糙集理論分別用于云模式下制造服務評價指標的主、客觀賦權。然后采用基于最大熵原理的組合系數模型，集成主、客觀賦權結果對云制造服務評價的影響。

2.1 G1-法求取指標權重

G1-法是一種通過主觀排序和兩兩比較賦值反映指標重要程度的賦權方法[9]，主要步驟包括：

(1)確定服務時間、成本、質量、可靠性、經營狀況和評分等云制造服務評價指標的主觀權重并按降序排列，即a1>a2>…>an。

(2)根據表1給出相鄰云制造服務評價指標ak-1與ak相對重要程度之比的理性賦值rk，即：

ωk-1/ωk=rk(k=n,n-1,…,3,2) (4)

(3)計算權重系數ωk，即：

(5)

ωk-1=rkωk(k=n,n-1,…,3,2)

(6)

根據公式(5)可獲得云制造服務評價指標a6的權值系數ω6，代入公式(6)反復迭代，可依次獲得各云制造服務評價指標的權重系數ω5,ω4,ω3,ω2,ω1。

2.2 變精度粗糙集模型

本文采用抗干擾能力較強的變精度粗糙集模型對云模式下制造服務評價指標進行客觀賦權[4]。

云制造服務評價信息決策表為：

I=(U,L=A∪W,V,F)

(7)

式中，U為云制造可行服務有限論域的非空子集，p條歷史交易記錄記為U={x1,x2,…,xp}；L為云制造服務屬性集；A={a1,a2,…,a6}為6個服務評價指標屬性集；W={a7}為服務決策屬性集；V為L的值域；F為各個服務屬性到值域的映射函數。

設Xg=U/A={X1,X2,…,X|U/A|}為云制造可行服務集U通過6個指標屬性集A劃分得到的等價類，Yh=U/W={X1,X2,…,X|U/W|}為U通過決策屬性集W劃分得到的等價類。若存在Xg?Yh，則Xg關于Yh的相對錯誤分類率為：

(8)

式中，|Xg|為等價類Xg中可行制造服務組合的個數。

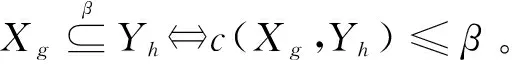
在β∈[0,0.5)時，Yh關于A的β的下近似為：

(9)

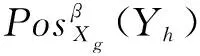
云制造服務指標屬性的信息量表示該指標對組合服務集的分類能力，信息量的大小反映了分類能力的強弱。任一服務指標ad的信息量γ(ad)為：

(10)

云制造服務指標屬性的被依賴度表示該指標屬性被決策屬性分類依賴的程度，被依賴度越大則該指標越重要。任一服務指標ad的被依賴度λ(ad)為：

(11)

(12)

2.3 主、客觀集成賦權

賦權法分為乘法賦權法和加法賦權法。乘法賦權法存在“倍增效應”，這里采用加法賦權法。常見的加法賦權法在分配各方法權重時較為主觀，不能發揮多個目標的效用，本文采用基于最大熵原理的集成賦權方法。

云模式下制造服務評價指標的真實權重在數理統計中為一個隨機變量，不同的主、客觀賦權方法所得的權重則是該隨機變量的一個樣本值，賦權方法的組合系數則是對應樣本的發生概率[10]。在已知制造服務評價指標信息的前提下，概率的合理分布可通過最大化熵求得。廣義距離和指云制造服務組合方案的指標參數值與理想值的加權距離和，其值越小代表評價對象整體越接近理想值。因此，基于最大熵原理的賦權方法集成了最大化熵和最小化廣義距離和兩個方面。

構造基于最大熵原理的集成賦權方法的組合系數模型為：

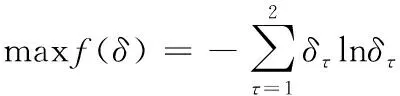
(13)

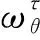
μ1為拉格朗日乘子，構造拉格朗日函數，通過歸一化和駐值條件求解全局最優解為：

(14)

對偶規劃為：

(15)

3 實例分析

在云模式下，某制造任務可分解為5個粒度適中的子任務，每個子任務可選擇的可行服務依次為2、3、6、3、2個。根據式(1)～式(3)，對216種云制造服務組合方案的評價指標T、C、Q、R、S和E進行歸一化處理，結果如表2所示。

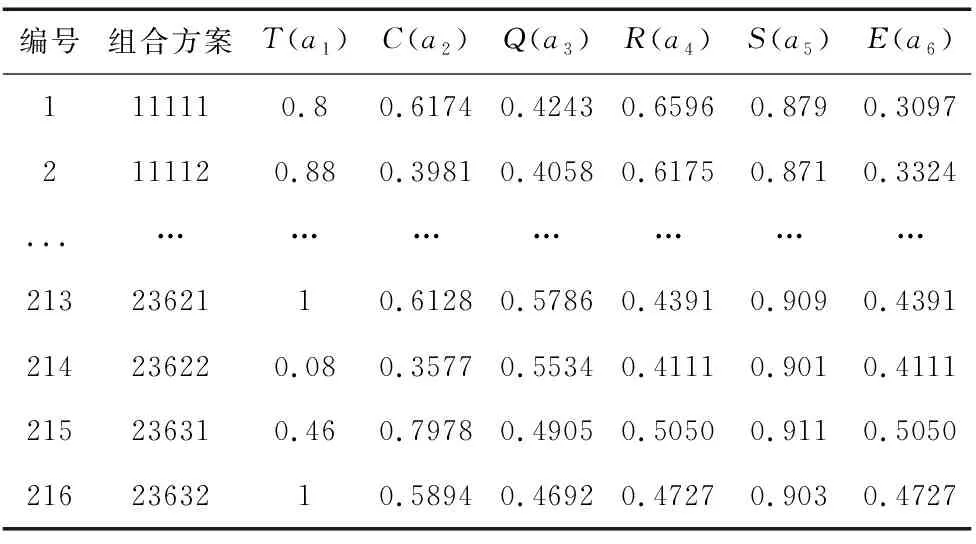
表2 云制造服務組合方案的評價指標參數(部分)

3.1 客觀賦權法

從歸一化處理后的云制造服務組合方案中隨機提取12條歷史記錄，采用K-means聚類方法對其進行聚類化預處理[11]，并將聚類序號寫入參數后的括號中，結果如表3所示。

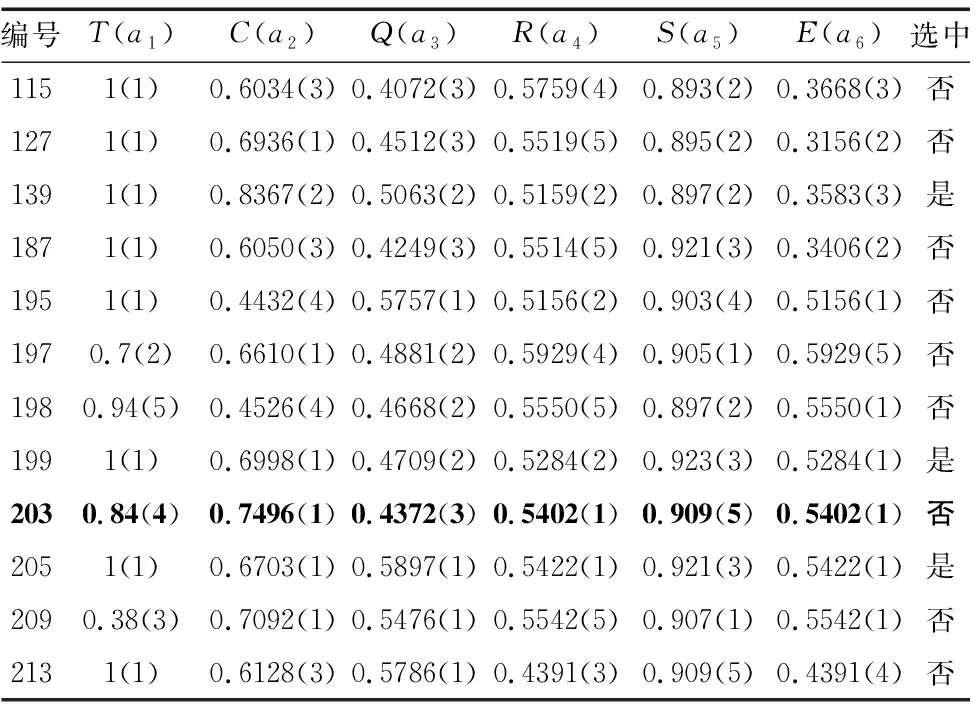
表3 聚類后的云制造服務組合方案評價指標參數

以原編號203組合方案的服務時間T為例，闡述變精度粗糙集模型中云服務指標屬性的信息量和被依賴度的計算過程。“0.84(4)”表示該組合方案的評價指標a1歸一化數值為0.84，聚類序號為4。

表3中被選中的決策類Y1=U/d1={x3,x8,x10}，未被選中的決策類Y2=U/d2={x1,x2,x4,x5,x6,x7,x9,x11,x12}。根據評價指標屬性a1劃分的等價類為X={X1,X2,X3,X4,X5}={{x1,x2,x3,x4,x5,x8,x10,x12},{x6},{x7},{x9},{x11}}，由式(10)可得：

γ(a1)=(82+12+12+12+12)/122=68/144

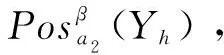
同理可得：λ(a1)=9/12，λ(a3)=7/12，λ(a4)=9/12，λ(a5)=10/12，λ(a6)=8/12。

將云服務指標屬性的信息量和被依賴度代入公式(12)可得各指標的客觀權重為ωa=[0.25,0.20,0.14,0.12,0.14,0.15]。

3.2 主觀賦權法

由G1-法獲得6個云制造服務評價指標的主觀排序為：

根據表1對相鄰服務指標進行理性賦值，即：

r2=ω1/ω1=1.2，r3=ω2/ω3=1.4，r4=ω3/ω4=1.1，r5=ω4/ω5=1.1，r6=ω5/ω6=1.2。

代入公式(5)，得：

將ω6代入公式(6)反復迭代，可依次獲得各云制造服務指標的權值系數分別為ω5=0.1271，ω4=0.1397，ω3=0.1538，ω2=0.2153，ω1=0.2582。

因此，6個云制造服務評價指標ak(k=1,2,…,6)的主觀賦值保留兩位小數后為ωb=[0.26,0.22,0.15,0.10,0.13,0.14]。

3.3 集成賦權法

采用Matlab對基于最大熵原理的集成賦權模型進行仿真，結果如表4和圖1所示。廣義距離和Cs的上下界3.745和3.731分別對應單一目標最小廣義距離和與最大熵，折線區間為兩個目標均起作用的有效解。分析可知，隨著廣義距離和Cs的減小，組合系數的差異增大，評價結果的差異變小。

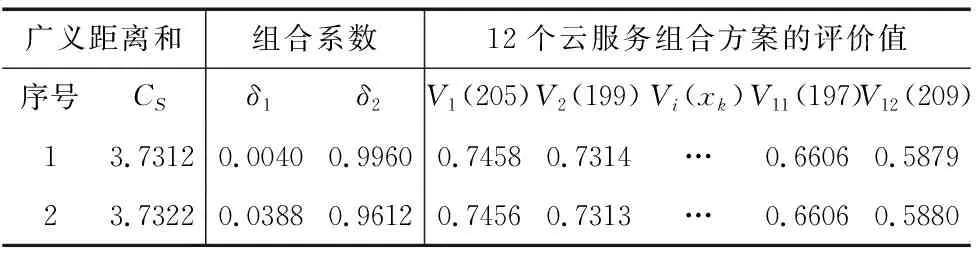
表4 基于最大熵原理集成賦權方法的組合系數和評價值

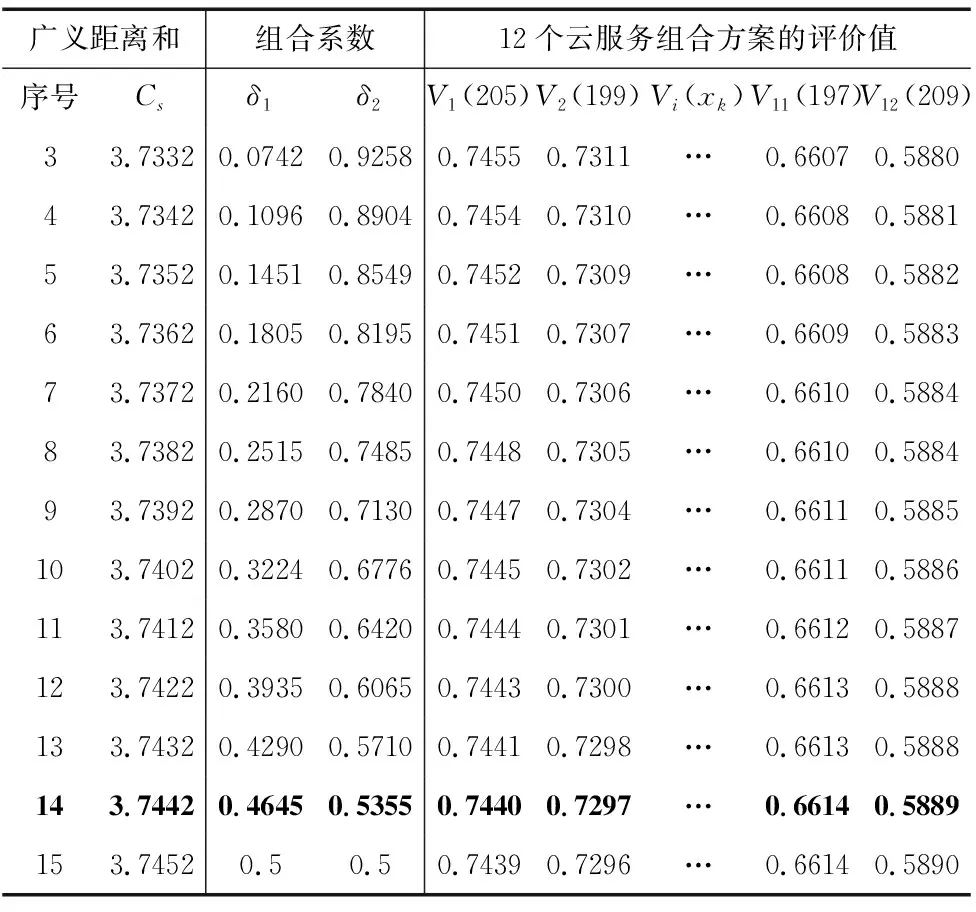
續表

選取廣義距離和Cs=3.744進行分析，此時δ1=0.4645，δ2=0.5355。集成主、客觀兩種賦權方法，云制造服務評價指標的最終權重為ω=δ1ωa+δ2ωb=[0.26,0.21,0.16,0.11,0.13,0.14]，云制造服務組合方案排序結果為205>139>199>213>203>127>195>187>115>198>197>209。

圖1 云制造服務組合方案的評價值

將文獻[3]的AHP法和熵值法應用于本案例，獲得ωa=[0.38,0.23,0.13,0.08,0.09,0.09]，ωb=[0.24,0.03,0.12,0.21,0.33,0.07]，綜合賦權為ω=[0.31,0.13,0.12,0.15,0.21,0.08]，用于表4可得排序結果為：

205>139>199>213>115>203>127>195>187>198>197>209。

比較兩種方法發現，僅方案115的排序從第9位前移至第5位，其他方案的排序保持不變。選中的方案為205、139和199，因此這種變化不影響云制造服務組合方案最終的選擇結果。

將文獻[3]的組合賦權用于表2可得排序為205>211>139>199>175>169>19>55>67>47>49>7>33>43>213。將本文集成賦權用于表2可得排序為12>211>205>139>199>175>67>19>33>169>55>47>7>36>213。根據交易記錄可知，優于方案199一定可行，弱于方案213則一定不可行，因此兩種方法均未將方案213之后的方案列出。分析發現，交易歷史所選中的方案位列兩種方法全部方案的前五名，符合優選條件；同時，優于方案213的所有方案僅有兩個存在不同，兩種方法的評價結果差異不大。本文所提方法具有良好的優選性能。

4 總結

首先將G1-法和變精度粗糙集理論兩種主、客觀賦權法，分別用于云模式下制造服務評價指標賦權；然后采用基于最大熵原理的組合系數模型，集成兩種賦權評價結果，協同主、客觀賦權法對云制造服務評價的影響。最后通過實例分析和比較研究，驗證了基于最大熵原理集成賦權方法的正確性和可行性。本文所提方法解決了傳統綜合賦權法因依賴主觀而可靠性不高以及未能發揮主、客觀兩種賦權方法作用的問題，具有良好的優選性能。本文所采用聚類方法適用于中小規模數據，后續將對聚類方法進行深入研究，并探討該方法較啟發式算法的優越性。