羽毛球拍網(wǎng)面振動(dòng)的理論與仿真分析
林 青,嚴(yán)舒芯,程 磊
(1.南京林業(yè)大學(xué) 體育部,江蘇南京 210037;2.南京林業(yè)大學(xué) 機(jī)械電子工程學(xué)院,江蘇南京 210037)
隨著國(guó)民經(jīng)濟(jì)的迅速增長(zhǎng),人民生活水平不斷提高,體育活動(dòng)越來越受到人們的青睞,尤其羽毛球運(yùn)動(dòng)普及較廣,成為老少皆宜的運(yùn)動(dòng)形式。出于對(duì)羽毛球運(yùn)動(dòng)的喜愛,人們對(duì)羽毛球球拍的選擇越來越重視,在球拍的研發(fā)過程中, 不僅需要綜合考慮球拍的重量、平衡、硬度、彈性等重要因素,尤其需要研究球拍網(wǎng)面的性能[1]。本文運(yùn)用膜振動(dòng)理論和有限元分析方法對(duì)羽毛球拍網(wǎng)面的性能進(jìn)行分析,以期為專業(yè)運(yùn)動(dòng)員了解拍面性能,發(fā)揮球拍的最佳效果以提高運(yùn)動(dòng)效率提供理論依據(jù)。
1. 羽毛球拍網(wǎng)面的理論分析
1.1 膜振動(dòng)理論
膜結(jié)構(gòu)是20世紀(jì)70年代發(fā)展起來的一種新型的張力結(jié)構(gòu)形式,它具有剛度小、重量輕等特點(diǎn),膜振動(dòng)就如同鼓上的鼓皮在敲擊下產(chǎn)生振動(dòng)一樣[2-4]。進(jìn)行圓膜的振動(dòng)理論分析時(shí),首先,在直角坐標(biāo)下,通過受力分析以及牛頓第二定律建立膜振動(dòng)的平衡方程;其次,考慮到在直角坐標(biāo)下的方程求解比較復(fù)雜,可將其化成在極坐標(biāo)下的圓膜振動(dòng)方程,利用分離變量法將方程轉(zhuǎn)換成零階貝塞爾方程標(biāo)準(zhǔn)式,通過求解得到圓膜的位移表達(dá)式;然后,通過施加圓膜的邊界條件推導(dǎo)出圓膜簡(jiǎn)正頻率方程,計(jì)算出各階的頻率。
設(shè)一張緊的膜處于xy平面上,在膜上取一個(gè)曲邊四邊形,膜四邊所受的力稱張力記為T,單位為N/m。
假設(shè)當(dāng)膜受到與xoy面相垂直方向的外力作用后,在張力T的作用下,產(chǎn)生垂直方向的振動(dòng)。面單元dxdy在橫向振動(dòng)時(shí),膜邊緣都受到張力的作用,張力與膜的切線方向一致,張力T與x軸的夾角為β,張力T與y軸的夾角為α。根據(jù)牛頓定律,作用在面單元dxdy的外力和膜振動(dòng)時(shí)產(chǎn)生的慣性力的合力應(yīng)等于零。面單元在直角坐標(biāo)系的受力分析圖如下(圖1)。
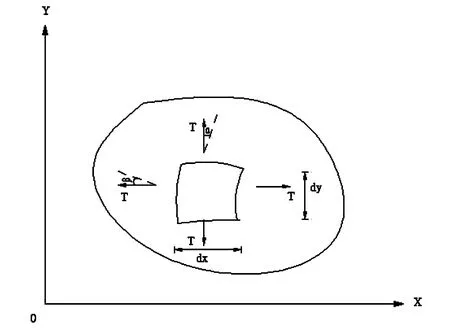
圖1 直角坐標(biāo)系面單元受力圖
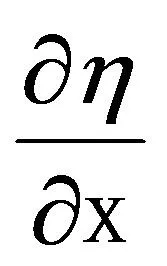
因此可解得作用于面單元四個(gè)邊緣的凈力合力為
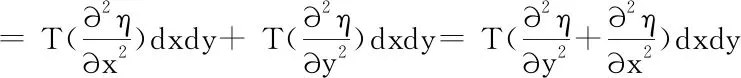
(1-1)
設(shè)σ為面密度,則面單元的質(zhì)量為
dm=σdxdy
(1-2)
面單元振動(dòng)的加速度為
(1-3)
根據(jù)牛頓第二定律得
F合=dm·a
(1-4)
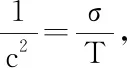

(1-5)
1.2 羽毛球拍面膜振動(dòng)的方程
羽毛球拍面近似為橢圓形且為網(wǎng)狀結(jié)構(gòu),本文將羽毛球拍面近似看成圓形膜且擊球時(shí)視為膜振動(dòng)。由于上式膜振動(dòng)方程是在xoy坐標(biāo)下的拉普拉斯方程,求解比較復(fù)雜,所以一般將其變換成在極坐標(biāo)下進(jìn)行求解[5-6]。

(1-6)
式1-6中θ—極角,r—極徑。極坐標(biāo)下膜振動(dòng)的微分方程為
(1-7)
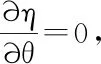
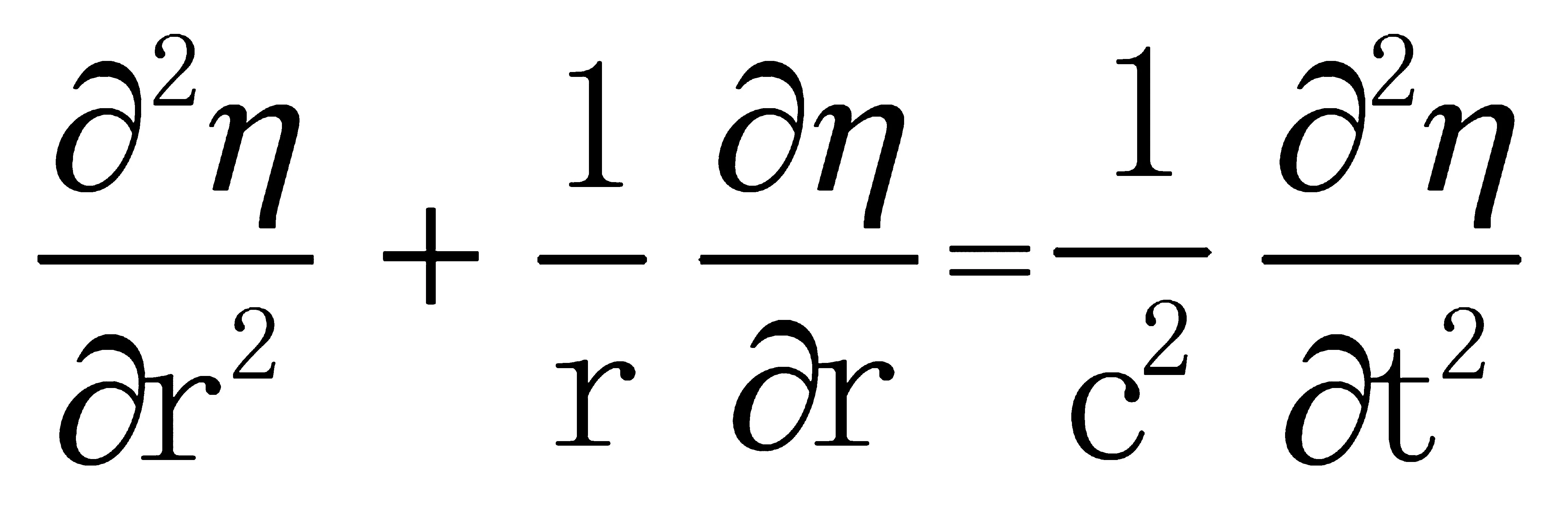
(1-8)
選用復(fù)數(shù)的形式[7],即令T(t)=ejωt并利用歐拉公式帶入1-8得
(1-9)
此方程式為零階貝塞爾方程的標(biāo)準(zhǔn)式[8]。其有零階貝塞爾函數(shù)和零階諾依曼函數(shù)兩個(gè)特解,所以該方程的一般解是兩個(gè)函數(shù)的線性組合即

(1-10)
所以1-9變?yōu)?/p>

(1-11)
考慮到諾依曼函數(shù)具有一個(gè)在零點(diǎn)發(fā)散的特性,即當(dāng)r=0時(shí),N0(0)→∞。對(duì)于具有張力的圓形膜而言,在圓心r=0處的振動(dòng)是有限的,則必須要求上式B=0,因此,1-10方程解為
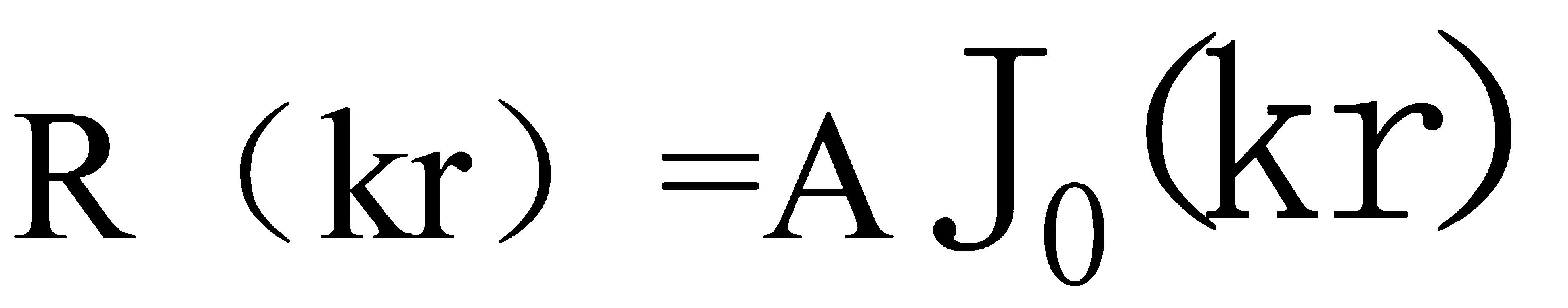
(1-12)
則膜的位移可表示為
(1-13)
將1-13方程變量換成x,得到貝塞爾方程為
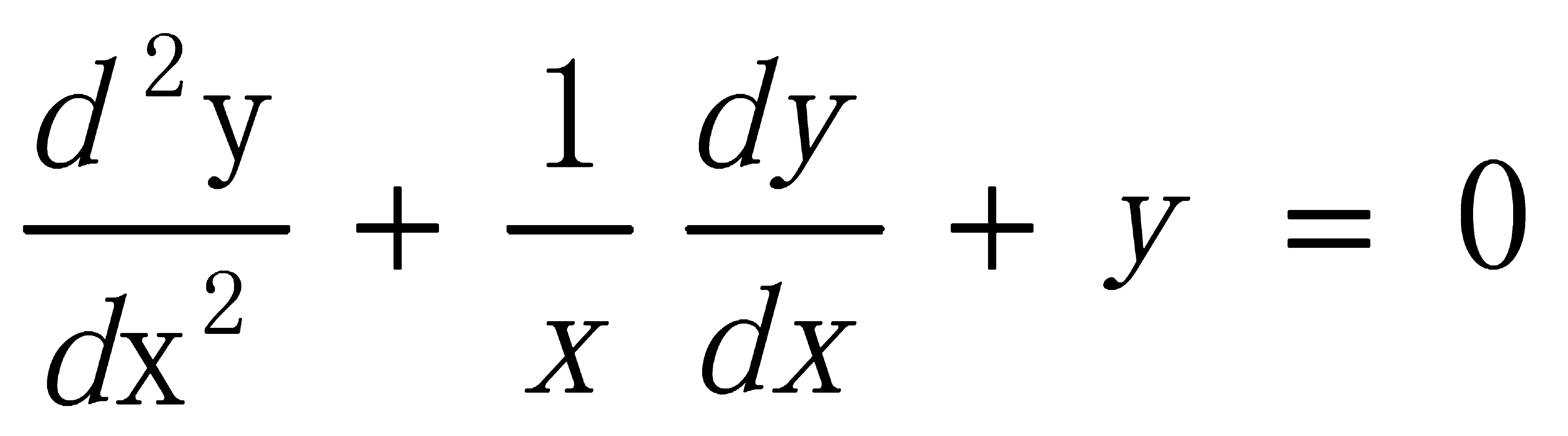
(1-14)
解得

(1-15)
令式中c=lnE,積分得
(1-16)
1.3 羽毛球拍面簡(jiǎn)正頻率的理論解
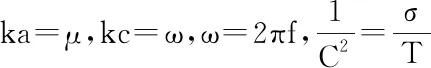
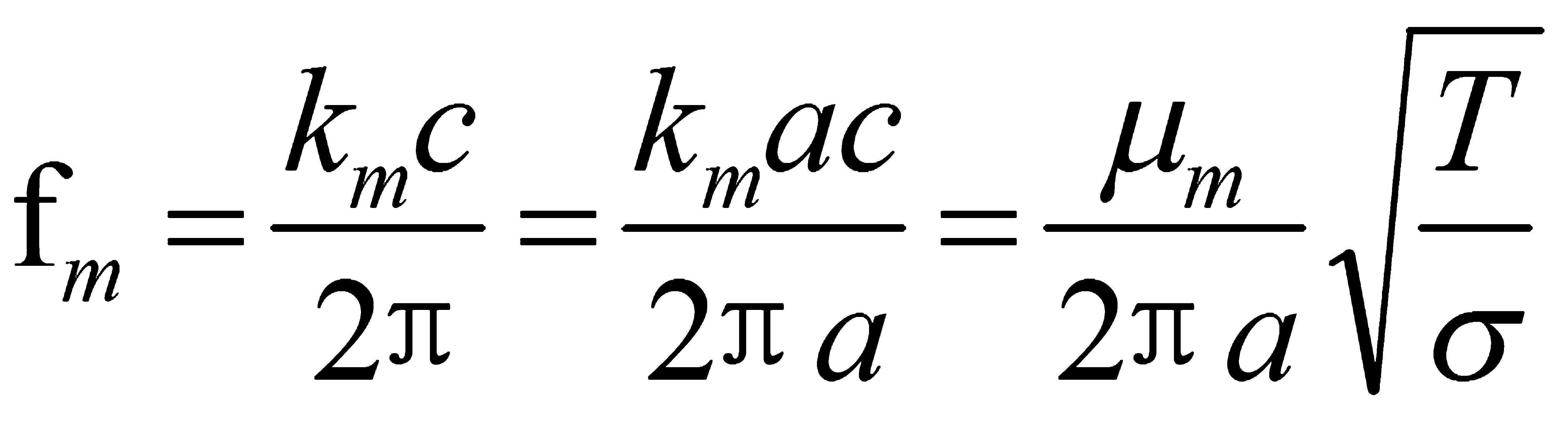
(1-17)
根據(jù)膜振動(dòng)理論可知,振型是根據(jù)不同的節(jié)圓數(shù)m和節(jié)徑數(shù)n所決定的。拍面作自由振動(dòng)時(shí),必將存在無數(shù)的簡(jiǎn)正頻率,其對(duì)應(yīng)的簡(jiǎn)正振動(dòng)方式為
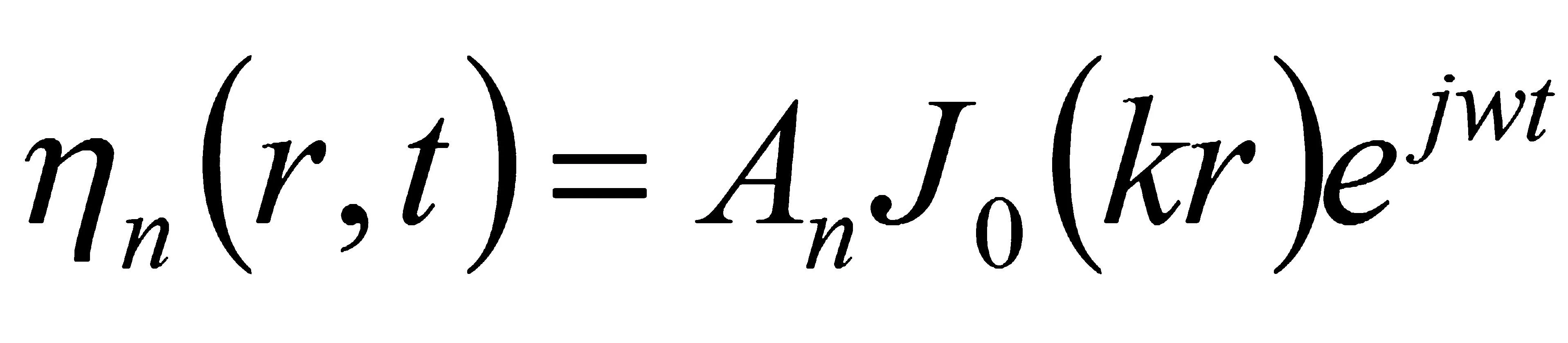
(1-18)
其實(shí)部為

(1-19)
由上式可求得圓膜對(duì)稱振動(dòng)的節(jié)線位置,令

(1-20)
解得零階貝塞爾函數(shù)的根值為
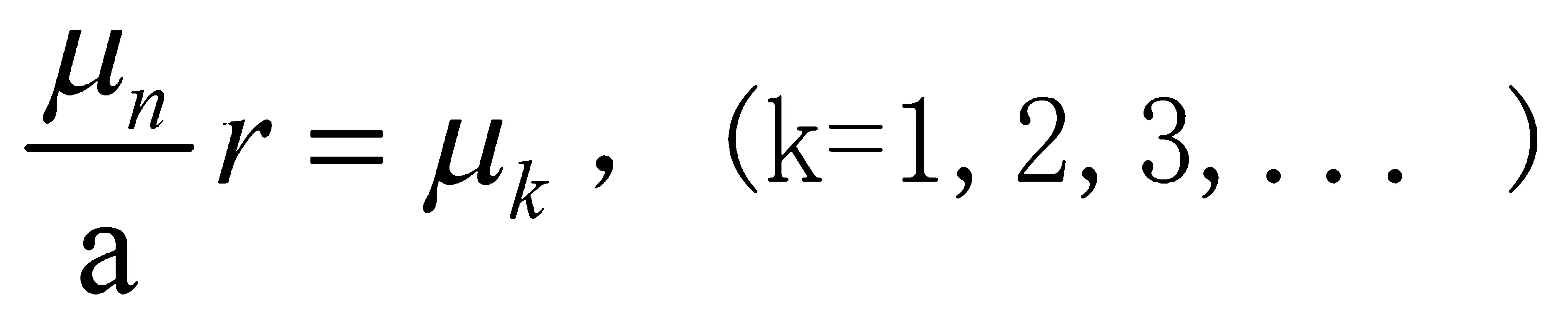
(1-21)
由此可得節(jié)線的位置為
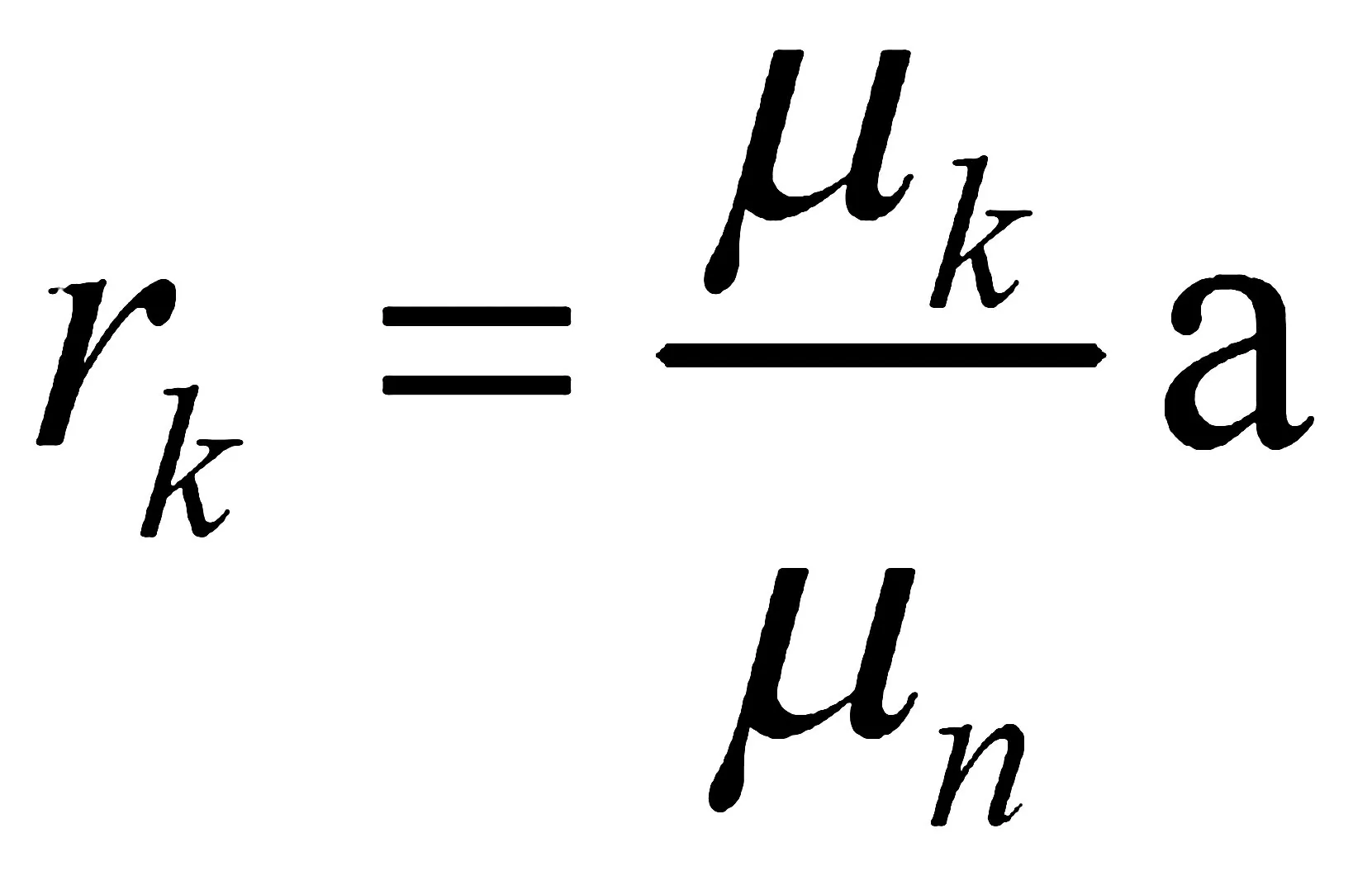
(1-22)
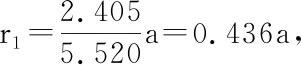
2. 有限元法及有限元分析軟件
2.1 有限元法
有限元法是利用數(shù)學(xué)近似的方法對(duì)真實(shí)物理系統(tǒng)(幾何和載荷工況)進(jìn)行模擬,通過簡(jiǎn)單而又相互作用的元素(即單元),就可以用有限數(shù)量的未知量去逼近無限未知量的真實(shí)系統(tǒng)。由于大多數(shù)實(shí)際問題難以得到準(zhǔn)確解,而有限元法不僅計(jì)算精度高,而且能適應(yīng)各種復(fù)雜形狀,因而成為行之有效的工程分析手段。有限元法的求解過程如圖2所示。

圖2 有限元法求解過程
網(wǎng)面進(jìn)行自由振動(dòng)時(shí),在理論上會(huì)發(fā)生無窮階的陣型,但由于能量的衰減一般只考慮前幾階振型。網(wǎng)面在受力發(fā)生變形時(shí),因?yàn)樗矔r(shí)接觸時(shí)間短,我們無法以肉眼看到網(wǎng)面自由振動(dòng)的振型以及受力后網(wǎng)面變形量的大小。本文利用有限元法,通過有限元分析軟件ANSYS中的WorkBench對(duì)網(wǎng)面進(jìn)行模態(tài)和靜力結(jié)構(gòu)的仿真分析,將網(wǎng)面的振型和變形可視化。
2.2 有限元分析軟件ANSYS簡(jiǎn)介
ANSYS軟件是美國(guó)ANSYS公司研制的融結(jié)構(gòu)、流體、電場(chǎng)、磁場(chǎng)、聲場(chǎng)分析于一體的大型通用有限元分析(FEA)軟件,其在機(jī)械、電機(jī)、土木、電子及航空等領(lǐng)域被廣泛使用,是世界范圍內(nèi)增長(zhǎng)最快的計(jì)算機(jī)輔助工程(CAE)軟件。軟件由前處理、分析計(jì)算和后處理三部分組成,具體流程如圖3所示。通過使用該軟件,不僅能夠獲得準(zhǔn)確數(shù)據(jù),而且還能縮短設(shè)計(jì)周期,降低預(yù)算成本[9]。
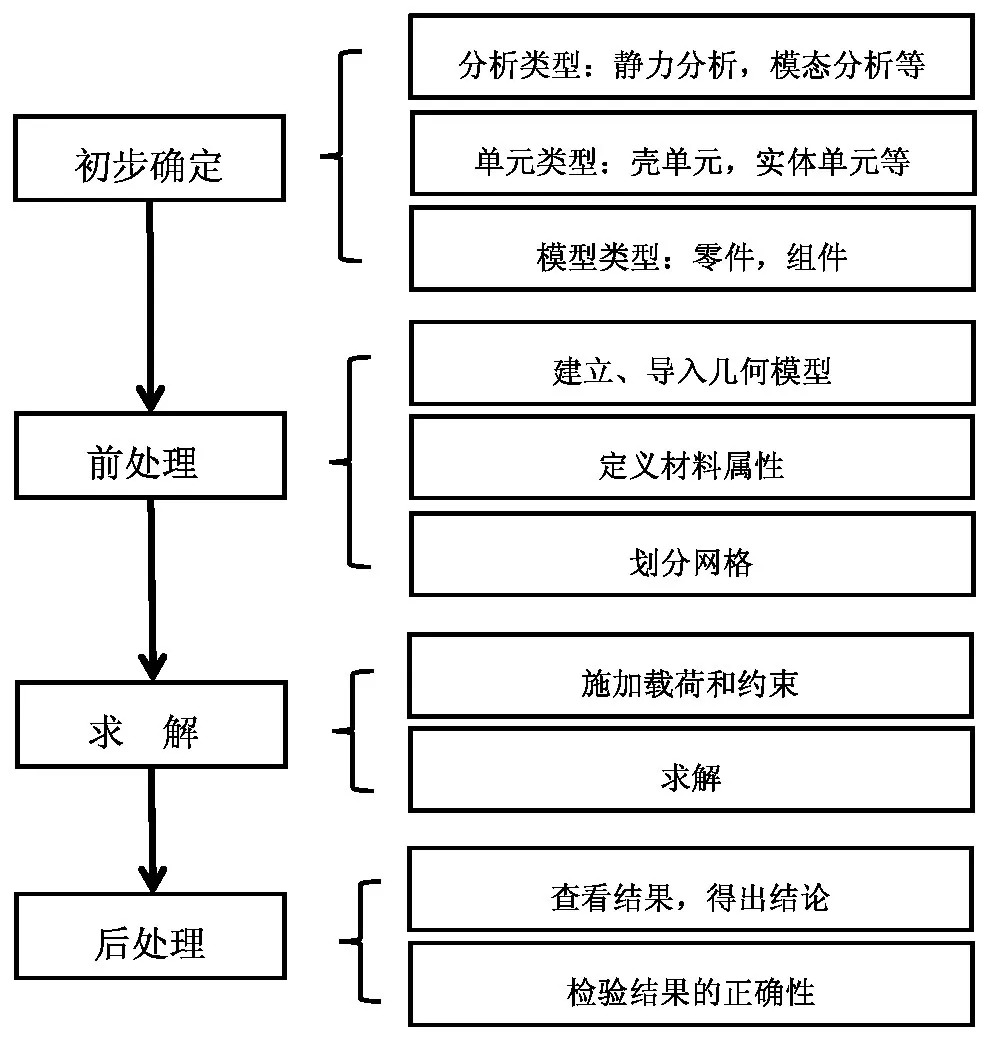
圖3 ANSYS軟件分析流程
ANSYS中的WorkBench是一種仿真平臺(tái)模塊,擁有各種與仿真分析相關(guān)的大型工程數(shù)據(jù)庫、求解器、建模工具以及后處理器等組件程序,同時(shí)具備參數(shù)管理和設(shè)計(jì)優(yōu)化功能,各項(xiàng)復(fù)雜的仿真任務(wù)都可以通過它實(shí)現(xiàn)。WorkBench中可以進(jìn)行結(jié)構(gòu)靜態(tài)分析、模態(tài)分析、非線性分析、屈曲分析、諧響應(yīng)分析、熱分析、轉(zhuǎn)子動(dòng)力學(xué)分析等。本文主要對(duì)羽毛球拍網(wǎng)面進(jìn)行模態(tài)分析和結(jié)構(gòu)靜態(tài)分析,并將計(jì)算結(jié)果與理論值進(jìn)行對(duì)比。
2.3 羽毛球拍網(wǎng)面模態(tài)分析
模態(tài)分析是指用模態(tài)坐標(biāo)去替換線性定常系統(tǒng)振動(dòng)微分方程組中的物理坐標(biāo),經(jīng)過方程組的解耦成為一組新的獨(dú)立方程。也就是說,模態(tài)分析的本質(zhì)是求矩陣的特征值,其“階數(shù)”就是特征值的個(gè)數(shù),將特征值從小到大排列就是階次。實(shí)際的分析對(duì)象是無限維的,所以其模態(tài)具有無窮階。但是對(duì)于運(yùn)動(dòng)起主導(dǎo)作用的只是前面的幾階模態(tài),所以計(jì)算時(shí)只要根據(jù)需要計(jì)算前幾階即可。
模態(tài)分析是動(dòng)力學(xué)分析最為基礎(chǔ)的一種,模態(tài)分析用于確定機(jī)械零部件的振動(dòng)特性及結(jié)構(gòu)的自振頻率特性,包括結(jié)構(gòu)的固有頻率和振型,它們是結(jié)構(gòu)承受動(dòng)態(tài)載荷設(shè)計(jì)中的重要參數(shù)。本文應(yīng)用ANSYS的模態(tài)分析功能,對(duì)有預(yù)應(yīng)力的網(wǎng)面振動(dòng)進(jìn)行模態(tài)分析。
任何結(jié)構(gòu)系統(tǒng)都可以用下述動(dòng)力平衡方程來描述

(2-1)
式2-1中[M]——質(zhì)量矩陣
[C]——阻尼矩陣
[K]——?jiǎng)偠染仃?/p>

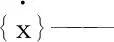
{x}——節(jié)點(diǎn)位移矢量
由于在對(duì)自由振動(dòng)的系統(tǒng)求解固有頻率和振型時(shí),阻尼對(duì)整個(gè)系統(tǒng)的影響會(huì)比較遲緩即可以忽略不計(jì),所以用ANSYS在進(jìn)行計(jì)算分析時(shí)選擇無阻尼模態(tài)分析。結(jié)構(gòu)在沒有阻尼作用下的動(dòng)力平衡方程為
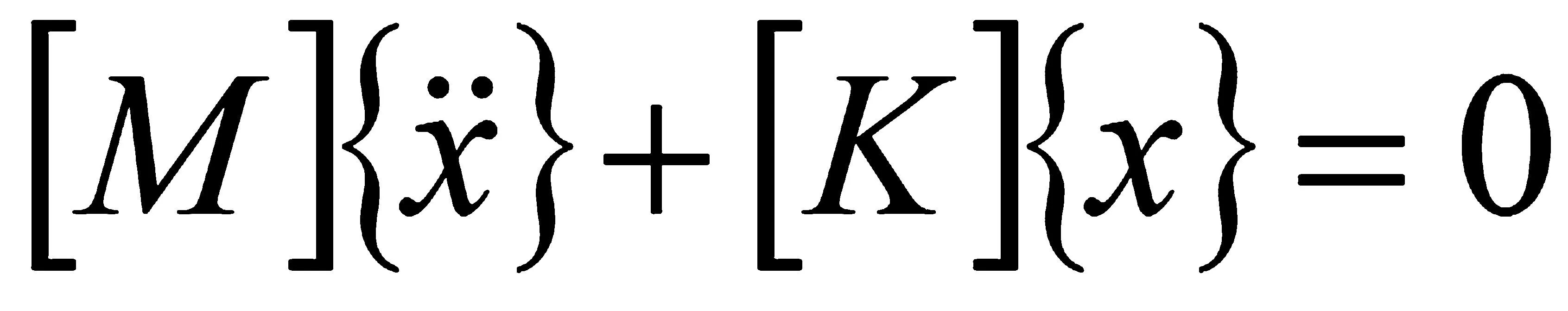
(2-2)
對(duì)于線性系統(tǒng),上式解的形式為
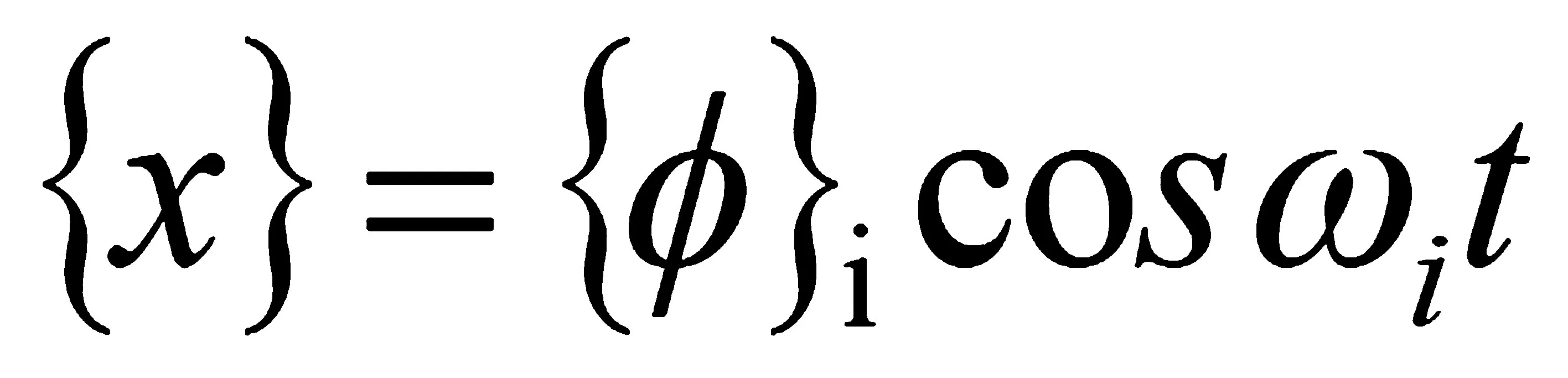
(2-3)
式中{Φ}i——第i階模態(tài)對(duì)應(yīng)的振型特征向量
ωi——第i階模態(tài)的固有頻率(單位為rad/s)
t——時(shí)間(單位為s)
將式2-3代入式2-2,得
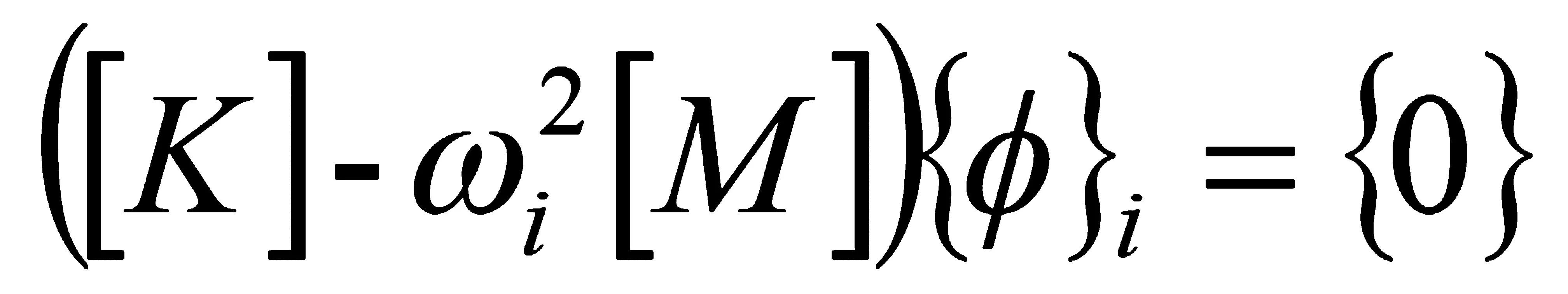
(2-4)
由于當(dāng)結(jié)構(gòu)自由振動(dòng)時(shí),各節(jié)點(diǎn)振幅不可能都為零,因此就相當(dāng)于求解系數(shù)行列式為零的解,即求其特征值。
2.3.1 前處理
2.3.1.1 創(chuàng)建分析項(xiàng)目
ANSYS WorkBench的工具箱中有多個(gè)分析項(xiàng)目,每個(gè)項(xiàng)目都分別顯示著分析的流程,從中可以觀察數(shù)據(jù)的流向以及分析的進(jìn)度。多個(gè)項(xiàng)目的對(duì)象可以相互連接,并提供了一個(gè)可視化的表示。本文用了靜力結(jié)構(gòu)分析和模態(tài)分析兩個(gè)項(xiàng)目,分別將兩個(gè)項(xiàng)目的工程數(shù)據(jù)、幾何模型、模型模塊連接,以及將靜力結(jié)構(gòu)分析中的解決方案模塊與模態(tài)分析中的設(shè)置模塊相連接,項(xiàng)目概圖如圖4所示。

圖4 創(chuàng)建分析項(xiàng)目
2.3.1.2 建立網(wǎng)面三維模型
由于在ANSYS WorkBench中可以直接導(dǎo)入SolidWorks的三維圖,所以本文使用SolidWorks工程設(shè)計(jì)軟件建模[10]。為了使ANSYS分析結(jié)果更加精確,確保模型的相似度是關(guān)鍵。根據(jù)國(guó)際羽聯(lián)羽毛球比賽規(guī)則,要求羽毛球拍面長(zhǎng)和寬分別不超過280mm和220mm。本文將拍面的外形近似為半個(gè)圓和半個(gè)橢圓組成。另外根據(jù)羽毛球拍網(wǎng)面穿線的特征,不難發(fā)現(xiàn)橫縱兩向中的所有相鄰線的穿法是相反的,并且整個(gè)網(wǎng)面不在同一平面內(nèi),每一根線都是由多段直線和圓弧構(gòu)成,因此網(wǎng)面的建模難度增加。本文通過手動(dòng)測(cè)量得到每段直線距離和相鄰兩根線的距離,通過已知的線徑、相鄰兩線距離和圓內(nèi)弦的垂直平分線過圓心三個(gè)條件找到圓弧的圓心,從而得到圓弧半徑,繪制圓弧草圖如圖5 所示,最后通過SolidWorks 三維建模中的掃描、陣列、拉伸、裁剪等特征功能完成網(wǎng)面的建模,三維圖如圖6所示。
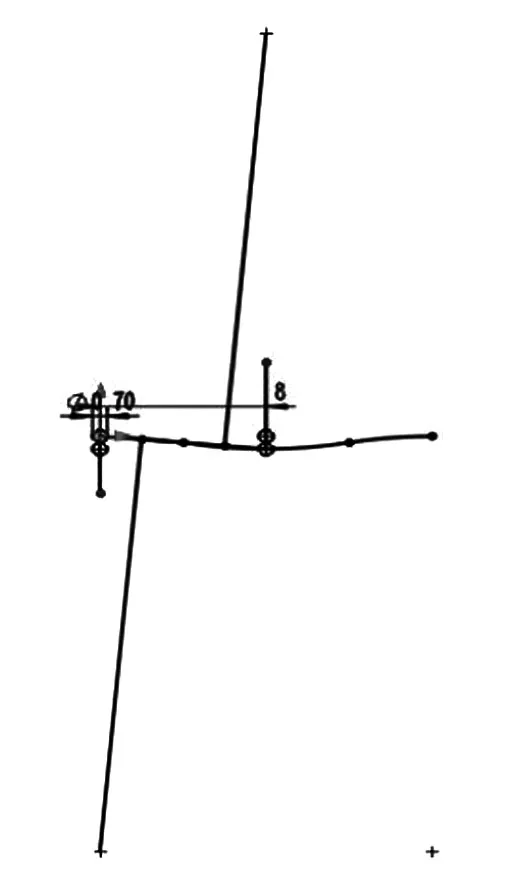
圖5 繪制圓弧草圖

(a) 網(wǎng)面局部三維圖

(b) 網(wǎng)面正視圖
圖6網(wǎng)面三維圖
2.3.1.3 網(wǎng)面材料的設(shè)定
由于WorkBench 材料庫中只有常規(guī)的材料,所以本文結(jié)合文獻(xiàn)[11]中的數(shù)據(jù),選用尤尼克斯BG65線加以計(jì)算,得到各參數(shù)值。通過手動(dòng)方式添加羽毛球線的材料性能,即尤尼克斯BG65線的密度、楊氏模量和泊松比,具體參數(shù)見圖7。
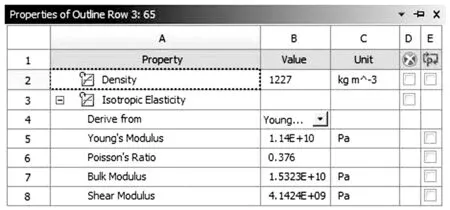
圖7 尤尼克斯BG65線的性能參數(shù)
2.3.1.4 網(wǎng)面的網(wǎng)格劃分
網(wǎng)格劃分是整個(gè)模態(tài)分析過程中至關(guān)重要的一個(gè)環(huán)節(jié),網(wǎng)格劃分質(zhì)量的好壞直接影響到后續(xù)計(jì)算分析結(jié)果的準(zhǔn)確性。劃分網(wǎng)格要進(jìn)行總體模型規(guī)劃,包括物理模型的構(gòu)造、單元類型的選擇、網(wǎng)格密度的確定等多方面內(nèi)容(見圖8)。本文中每根網(wǎng)線只受單一的拉伸力,精度要求不是很高,所以選擇自動(dòng)生成網(wǎng)格劃分,全局網(wǎng)格控制如下圖所示,網(wǎng)面網(wǎng)格劃分示意圖如圖9所示。
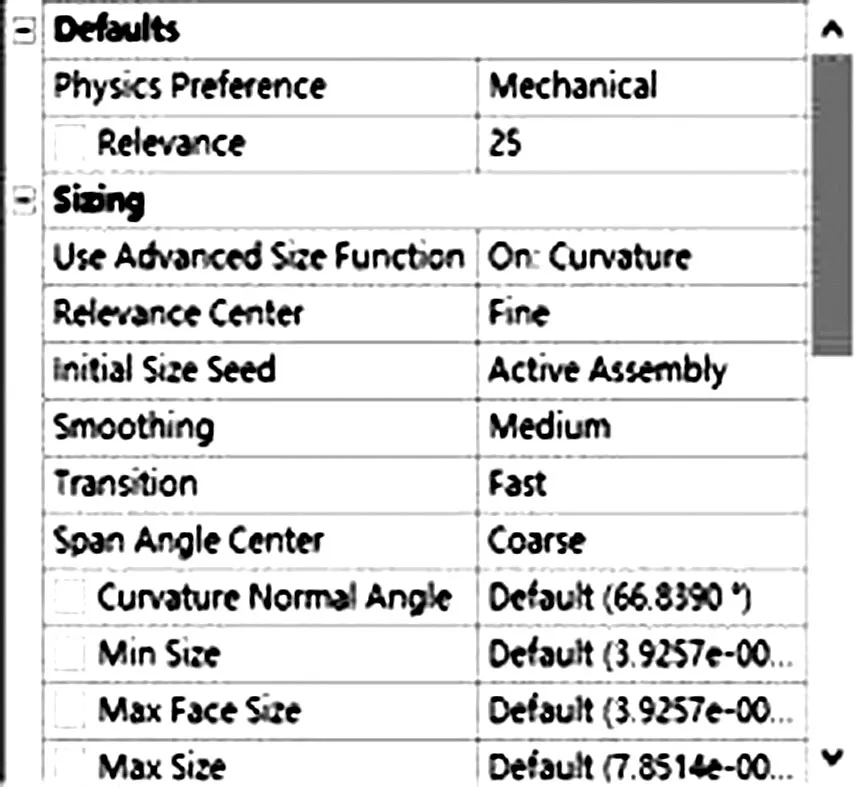

圖9 網(wǎng)面網(wǎng)格劃分
2.3.1.5 網(wǎng)面邊界條件的設(shè)置
邊界條件的加載也是至關(guān)重要的一個(gè)環(huán)節(jié),其加載的正確與否直接影響到模擬結(jié)果。根據(jù)分析中邊界條件是否隨時(shí)間變化的情況,其加載的容易程度也就不同。一般而言,邊界條件不隨時(shí)間變化的加載相對(duì)容易,但要施加隨時(shí)間變化的動(dòng)態(tài)載荷就會(huì)比較困難。對(duì)于本文中的網(wǎng)面來說,網(wǎng)面周圍一圈都要施加固定約束,并且每根線都受到向外的軸向預(yù)應(yīng)力,這里按業(yè)余選手水平設(shè)定羽毛球拍穿線磅數(shù)為21磅即93.5牛頓。圖10中,A代表固定、BCDE分別代表不同方向的預(yù)應(yīng)力。
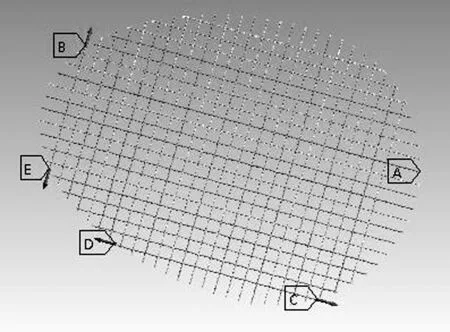
圖10 施加邊界條件
2.3.2 分析計(jì)算
在上述環(huán)境設(shè)定完成后,通過計(jì)算機(jī)直接求解可得網(wǎng)面各階振型圖,圖11所示為部分陣型圖。

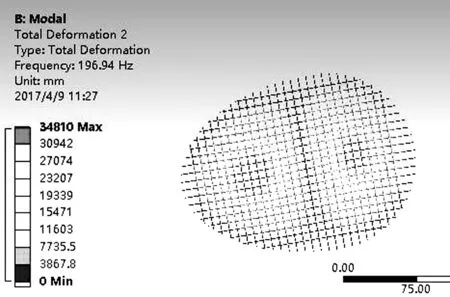
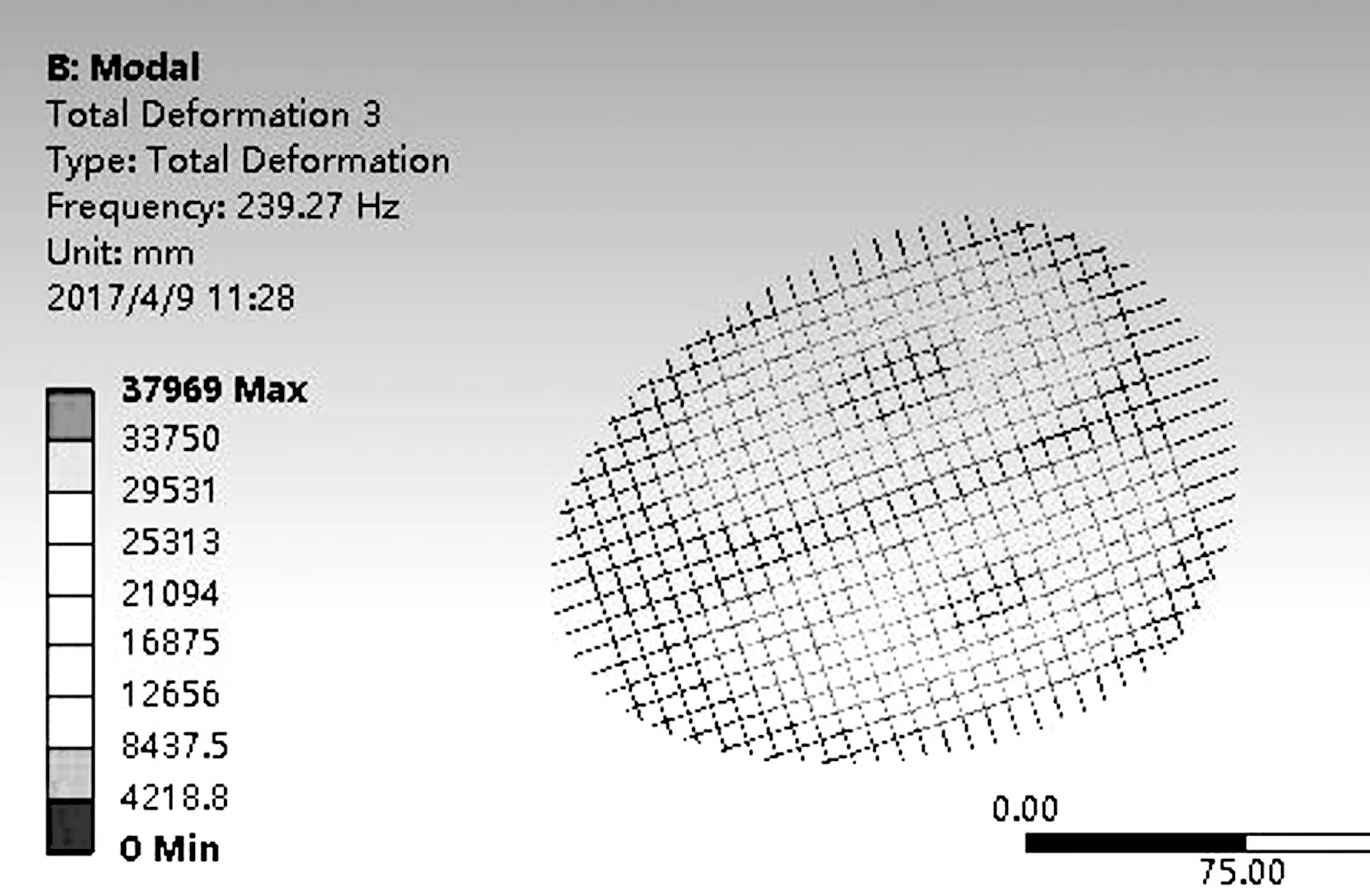
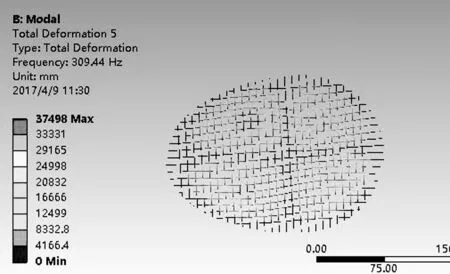
2.3.3 結(jié)果分析
為了驗(yàn)證將網(wǎng)面簡(jiǎn)化為圓膜假設(shè)的可行性,本文采用了理論和有限元計(jì)算兩種方法,分別對(duì)周邊固定、半徑為95mm并承受21磅的圓膜和同樣條件下的羽毛球拍網(wǎng)面,進(jìn)行固有頻率[12]與振型的求解。表1為其中兩階固有頻率的理論解與仿真計(jì)算值兩者對(duì)比。

表1 圓形薄膜與羽毛球拍網(wǎng)面固有頻率及振型
由表1可以看出,拍面前二階的理論解和仿真結(jié)果誤差較小,兩者得出的值雖然不完全相等,但都在同一個(gè)數(shù)量級(jí)。所以本文提出將羽毛球拍網(wǎng)面看作膜振動(dòng)的設(shè)想是可行的,產(chǎn)生的誤差有以下原因:
(1)理論計(jì)算是按照?qǐng)A膜的外形計(jì)算的,與羽毛球拍網(wǎng)面的實(shí)際形狀有差距;
(2)有限元計(jì)算時(shí),網(wǎng)面建模不能和實(shí)際拍面完全一致。
2.4 網(wǎng)面結(jié)構(gòu)靜力分析
圖12 創(chuàng)建項(xiàng)目分析

圖13 邊界條件施加
結(jié)構(gòu)分析是有限元分析中最常用、最普遍的一個(gè)應(yīng)用領(lǐng)域,它有七種結(jié)構(gòu)分析類型。靜力分析屬于結(jié)構(gòu)分析,它包括線性和非線性分析。與速度和加速度沒有關(guān)系的對(duì)象主要用靜力學(xué)分析來計(jì)算,它是研究靜平衡關(guān)系的一種。
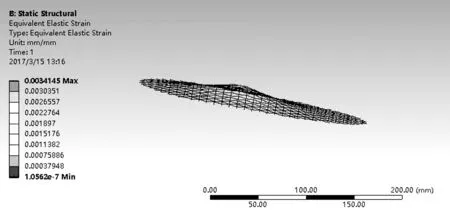
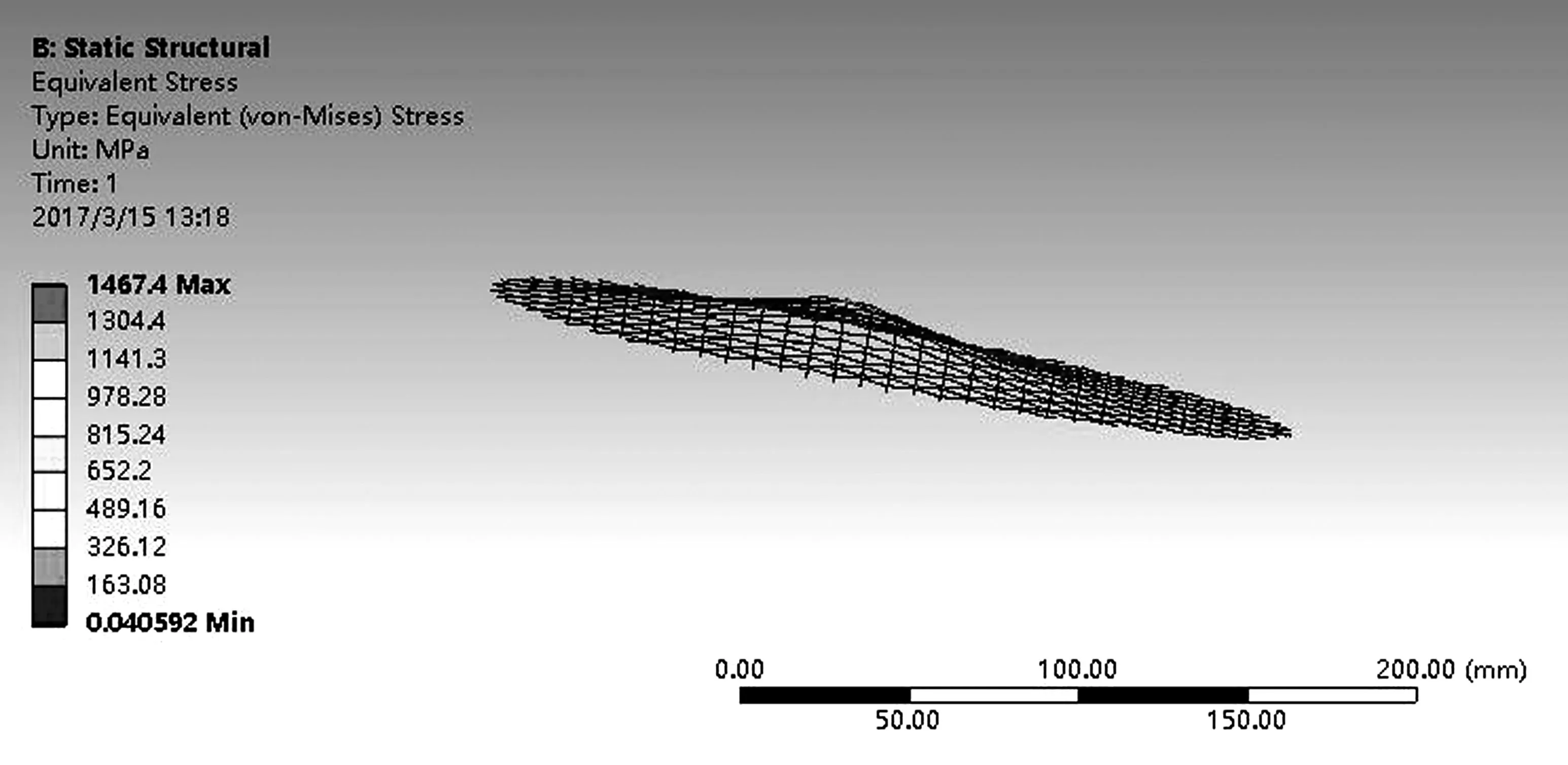
本文針對(duì)羽毛球拍網(wǎng)面進(jìn)行線性結(jié)構(gòu)靜力分析(見圖12),其分析步驟同模態(tài)分析類似,區(qū)別在于要將模態(tài)分析項(xiàng)目去除;用羽毛球拍擊球時(shí),相當(dāng)于網(wǎng)面在很短時(shí)間內(nèi)受到一沖擊載荷的作用,羽毛球重量約5克,擊球時(shí)間按0.04秒計(jì),擊球速度取280公里/小時(shí),經(jīng)計(jì)算網(wǎng)面受力約為9.8牛頓,所以在約束邊界條件時(shí),在中點(diǎn)施加垂直于網(wǎng)面、大小為9.8N 的載荷,邊界條件施加如圖13所示;最后進(jìn)行應(yīng)力、應(yīng)變和總變形求解,得到相應(yīng)的云圖(見圖14)。
由分析結(jié)果可得,在中點(diǎn)施加P0=9.8N的力,其最大變形為ε=0.716mm。
3. 結(jié)語
本文運(yùn)用膜振動(dòng)理論和有限元分析軟件,分別對(duì)羽毛球拍網(wǎng)面進(jìn)行了理論計(jì)算和仿真分析,得到了部分固有頻率和振型圖。通過對(duì)比可知,將網(wǎng)面看成膜的設(shè)想是可行的,可以用膜振動(dòng)理論對(duì)網(wǎng)面進(jìn)行理論分析;本文還利用ANSYS軟件對(duì)網(wǎng)面進(jìn)行了靜力結(jié)構(gòu)分析,得到了應(yīng)力云圖、應(yīng)變?cè)茍D和總變形云圖。以上工作為進(jìn)一步對(duì)網(wǎng)拍類球拍網(wǎng)面的研究提供了理論依據(jù)和有效方法,并可為專業(yè)運(yùn)動(dòng)員和業(yè)余選手了解拍面性能,發(fā)揮球拍的最佳效果以提高運(yùn)動(dòng)效率提供理論依據(jù)。
(a)應(yīng)力云圖
(b) 應(yīng)變?cè)茍D

