職高數學應用化教學模式探究

馬丹

摘 ?要：數學是嚴密細致的邏輯推導、結構嚴謹的知識體系，在數學教學中，教師常常希望學生能領會數學的精髓，由此及彼、由淺到深、步步遞進的操作、推導、解決問題。職高學生的數學基礎相對來說是比較差的，所以教師在教學中要根據學生的實際，淡化數學的嚴密性和系統性，增強數學的實用性和趣味性，進行數學的應用化教學。本文就從幾個實例入手，談談這種有益的教學嘗試。

關鍵詞：職高數學 ?應用化 ?教學模式

陶行知教育思想的核心為“生活教育”。他認為最好的教育就是從生活中學習。結合數學的特點，教師要把生活、數學、社會結合起來，讓學生在切身體會中感悟新知識，從而使課堂充滿生機。職高生已具有相當多的生活經驗，老師要巧妙運用學生在生活中的感知，激發學生的求知欲。

案例1：有趣的概率

例題：一個班共48位學生，在該班中，是“有兩個同學生日相同”的可能性大，還是“沒有任何兩位同學生日相同”的可能性大。

由計算結果可知，該班任何兩位同學生日都不相同的可能性只有4%左右，而有兩位同學的生日相同的可能性達到96%，所以該班極有可能有兩位同學生日相同。

本例總結：該例在于問題的情境簡單、清楚，容易引起學生的興趣。同一個班級里的學生出現兩個人同年同月同日生似乎是一個小概率事件，但計算表明，出現這種情況要比不出現的概率大得多，結論出人意料。這很容易使學生感受到數學的神奇魅力，對提升學習數學的興趣是很有幫助的。

應用拓展：概率論最是起源于人們對博彩的分析。在現實生活的有關事例是不計其數的，其中不乏富有趣味的例子。教學時就不妨找一些例子分析，讓課堂充滿神奇。

案例2：

例題：金字塔是人類歷史的奇跡。如圖1所示，金字塔的坡面是有角度的，這一角度制約著金字塔的高度。已知胡夫金字塔的底邊長為230.6米，塔高為146.5米，坡面的坡度是多少？金字塔的四個坡面均相同，底面為正方形。

本例分析：求坡面的坡度實際上是求坡面與地面的二面角的大小，所以關鍵是找出這個二面角。過金字塔的頂點作地面的垂線，得垂線與地面的交點—垂點，然后分過頂點和垂點作某一底邊的垂線，這兩條垂線相交所得的角即為坡面與地面所成的二面角。通過計算求得該角度為57.55°。

本例總結：還可以結合金字塔的種種有趣問題，以吸引學生興趣，相應的知識在網上方便查找。而本例最關鍵的步驟就是找出二面角，這是解決該問題的鑰匙。

應用拓展：在上例中要用到立體幾何中二面角的概念。雖然我們生活中的物體都是立體的，但是我們對物體的認識以及我們的思維往往是平面的。舉個腦筋急轉彎的例子，

問：能不能種三棵樹，使任意兩棵之間的距離相等？

我們一般很快就能回答說：“能，把樹種到等邊三角形的三個頂點上就行了。”

再問：能不能種四棵樹，使任意兩棵樹之間的距離相等？

我想了好久都覺得不能。事實上這是能做到的，只要把樹種到正四面體的四個頂點上就行了。

這一腦筋急轉彎表明，我們平時的思維并不是立體的，而是平面的。不通過立體幾何的學習，就很難對物體的空間位置關系有正確認識。在實際教學中發現，沒有一定的立體模型，學生憑自己的想象力，不易建立空間圖形的概念，難以形成較為準確的模型。這時，可以用網絡資源來突破這一難點，信息化時代網上有各種資源，不必自己動手做了（能熟練地在幾何畫板上作圖當然更好）。立體圖可以在屏幕上全方位向學生展示，如圖2所示就是一個可以演示上例中所說二面角動畫的三個截圖，通過動畫演示，學生很直觀地理解二面角的概念，結合動畫講解，可以使學生更好的掌握二面角的求法。

實例3數學在社會上的應用：個人所得稅的計算

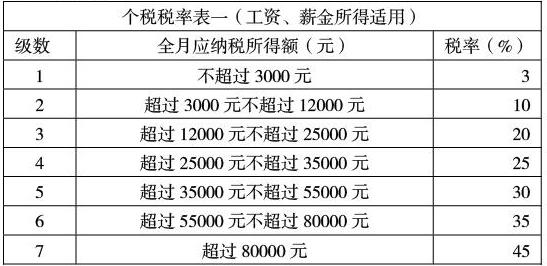
例題：××同學畢業后在一家公司上班，每月的薪水為8800元，按現行的個人所得稅制度，他每月要交多少稅？（個人所得稅稅率表見表一）

本例分析：個人所得稅的起征點為5000元，所以該同學的月收入中扣除5000元免征額后，剩下3800元需交個人所得稅，而這3800元中前面的3000元適用稅率為3%，稅款為3000×3%=90元，后面的800元適用稅率為10%，稅款為800×10%=80元。所以他每月所交個人所得稅為90+80=170元。

本例總結：學生不久以后就會走上社會遇到交稅問題。事關學生以后切身利益的值得一講。另外在生活中很多人并不清楚自己交了多少稅。課上給學生講這種實用的數學運算，也不失為在職高數學課堂進得有效教學的一個好策略。

應用拓展：學生畢業，會遇到各種各樣與錢有關的問題，比如存銀行的利息計算、水電費結算等數學問題。對學生打理事務、節省開支、投資理財都很有幫助，對學生的應用數學的能力培養來說，是十分有效的。

通過上面的三個實例可以發現，在數學教學的過程中，只要我們時時留意、處處留心，就可以發現在數學知識的海洋里，有著各種各樣的有趣的問題、巧妙的解答，在我們的生活中到處都是數學的用武之地。

實踐表明，職高數學課堂應用化的教學模式是學生樂于接受且有效的做法。畢竟，我們的現實生活中充滿了數學，數學不存在有沒有用的問題，只有會不會用的問題。

參考文獻

[1]中學數學課程教材研究開發中心.普通高中數學課程標準（實驗）[M].人民教育，2004.

[2]吳和貴，朱維宗，陳靜安.新課標下的數學課堂教學過程的優化[J].數學通報，2007（3）.