關于數形結合方法在高中數學教學中的應用

數學是高中最重要的一門學科，它是最能拉開學生分數差距的學科，但是數學又比較抽象化，導致很多學生聽不懂課，不會做題，從而厭惡對數學的學習。數學是一切科學的基礎，它能夠推動科學的進步、社會的變革，對國家的快速發展也有重要意義。這也有利我國科教興國戰略的實施。因此，在高中數學教學中，運用數形結合的是想方法是非常重要的，它能夠幫助學生更深入地理解和掌握數學知識，推動他們邏輯思維能力和思維敏捷性的發展。

一、高中數學教學中數學方法的應用現狀

1.運用數形結合思想方法常見的解題誤區

數形結合方法是解題的有效方法，它備受高中生喜愛，倘若使用不當，也會出現各式各樣的問題，例如畫圖草率，審題不明確，缺乏全面考慮，理解不深刻等都會把簡單的題目容易寫錯。數形結合方法簡潔、形象、快速，但是簡潔性會使學生忽略最優解，不能進行深入全面的思考；形象性會使學生粗心大意，分析不全面；快速性容易使學生計算失誤。因此，在運用數形結合方法時要準確抓住“數”和“形”的密切關系，仔細審題，堅持穩中求勝，同時不要讓數形結合方法固定你的思維，僵化你的思路，這不利于大腦創造性的開發，對以后的生活和工作都會產生不好的影響。

2.利用多種途徑培養高中生的數形結合思想

高中數學教材是抽象化和系統化的，高中數學課本中有大量的定義、概念，這都是比較抽象化的，學生不能正確理解，但是教材的編寫又是較為系統的，它把所要學習的數學知識的方方面面都以學生身心發展的特點和接受能力編排，這就要求教師把握數學教材的整體大綱，以課本為基礎，利用多種途徑去培養高中生的數形結合思想能力。例如通過實際操作觀察培養學生對幾何體的感知。

3.數形結合方法的教學策略研究

教學的主體是學生和教師，這就要求教師改變以往落后的教學方式，學生轉變學習方法，才能有效運用數形結合方法快速準確解題。以往的教學方法是輕視過程，重視結果，這是非常不可取的，它沒有深度的挖掘數形結合的現實意義和教育價值。學生做題容易眼高手低，粗心大意，這就要求教師轉變刻板的教學方式，學生也要更加仔細和認真，畢竟一個小數點的錯誤就會影響到整個題目最后的結果。

數形轉化是運用數形結合方法解題的關鍵，在面對不等式求集合問題時，可以運用數形結合的方法，這不但能縮小計算量，也能保證答案的準確性。教師要通過實際練習提高學生數形轉化的能力，使學生能夠“以形聯數，見數想形”，促進學生對數學知識的理解，增加解決問題的經驗。

二、數學結合方法在高中數學教學中的實際應用

1.在集合中的應用

集合是高中數學課的第一課，它對后面的學習有基礎性的作用，在集合中運用數形結合方法，能夠把抽象的代數關系轉變為直觀形象的圖形關系，能幫助學生更加深入的了解幾何知識。例如處理集合間的包含關系時，可以把兩個集合表示在X數軸上，并在對應的點標上數字或字母，根據數軸上的大小關系，列出不等式組進行解答。

在解決已知條件不清晰且含有未知數的集合時，使用數軸來解決，把已知條件標在數軸上，觀察它們的交集、并集、子集。

2.在三角函數中的應用

例如，比較sin20°和cos20°的大小。

方法一：cos20°=cos(90°—50°)=sin50°

y=sinx在x∈[0,π/2]為增函數

∵0＜20°＜50°＜90°

∴sin20°＜sin50°

即：sin20°＜cos20°

方法二：

X∈[0,π/2]

解：由圖可知：sin20°＜cos20°

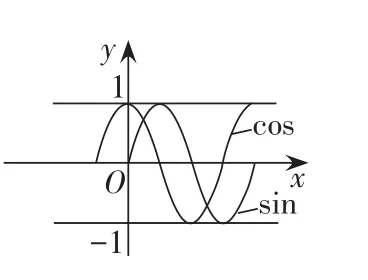
從例題可以看出，在三角函數中，運用數形結合思想有利于把抽象的代數轉化化為簡單明了的圖形，這有助于學生理解和掌握三角函數的知識，把理論與實際相聯系，促進邏輯思維能力的提高和空間想象能力的發展。

3.在解析幾何上的應用

解析幾何的發展離不開數形結合的支撐，解析幾何高中數學較難的一部分，并且高中的解析幾何研究的就是曲線與方程的問題，因此在解題時要牢牢抓住曲線與方程之間的關系，靈活運用數形結合方法。數形結合思想是解析幾何發展的基礎，學生要把握這一關系，讓學生感受到數形結合方法對解決解析幾何問題的優勢，體會數形結合方法在數學中解決問題的魅力。

運用數形結合解決解析幾何主要有三個步驟：(1)建立空間或平面直角坐標系。(2)用代數條件表示幾何條件。(3)把用代數得出來的結果用幾何表示。

三、結束語

數形結合方法是解決數學問題的有效方法，但在高中數學教學上，還不能得到較好的運用，學生不能體會到數形結合思想的巧妙之處，并且高中生是受教育的主體，這說明高中教育的改革勢在必行，必須要打破傳統的教學方式，給教師和學生更大的自主發揮的空間，提高學生解決問題的效率和準確性，促進學生創造力的發展和邏輯思維能力的提高，為他們未來的發展打下堅實基礎。