聲子晶體負泊松比蜂窩基座的減振機理研究

秦浩星　楊德慶

摘要： 通過建立聲子晶體負泊松比蜂窩基座的等效動力學模型，研究該基座局域共振減振機理。探討動力學參數（固有頻率比、質量比、阻尼比）、聲子晶體的周期層數等對基座減振性能的影響規律。研究結果表明，當聲子晶體固有頻率與基座固有頻率接近時，能有效降低基座發生結構共振時的響應幅值。建立聲子晶體蜂窩基座的優化設計模型，優化得到具有指定局域共振固有頻率的聲子晶體結構。動力學頻響計算表明，該優化設計基座能夠有效抑制結構的低頻共振現象。

關鍵詞： 減振; 聲子晶體; 負泊松比; 蜂窩; 基座

中圖分類號： U661.44; O735? 文獻標志碼： A? 文章編號： 1004-4523（2019）03.0421.10

DOI：10.16385/j.cnki.issn.1004.4523.2019.03.006

引 言

船舶大型化發展趨勢，造成船體結構固有頻率隨之降低，而船舶動力設備載荷的峰值主要集中在低頻段，這將導致船體共振現象和振動響應幅值顯著增加。此外低頻振動線譜分量能量較大，輻射距離遠，是影響艦艇隱蔽性的主要因素。常見的單層、雙層、浮筏、浮艙、浮動地板等減振隔振裝置，存在著低頻減振效果不好、不能適應外擾變化等缺點[1]，傳統的減振設計方法有隔振、吸振和阻尼減振技術等[2.3]。基座是支承船舶動力設備的重要結構，在保證其結構強度的前提下，適當減小其剛度有利于提高減振效果，通過對基座進行減振設計來降低船舶結構振動是有效途徑之一[4.5]，主要是通過改變基座自身結構形式和尺寸以達到減振效果[6]。

負泊松比材料具有不同于普通材料的獨特性質，其高空隙率和低密度的特點，在結構輕量化與減振降噪方面有廣泛應用[7.8]，成為工程領域不可缺少的材料之一[9.11]。圍繞泊松比效應材料在結構動力學方面的特性，以下學者做了相關的研究：李永強等[12.13]研究了蜂窩夾層板主共振情況下的非線性動力學特性，分析了不同結構參數對動力學特性的影響。Hnig等[14]研究了正六角蜂窩結構的面內抗沖擊性能。Banerjee等[15]利用等效連續介質模型研究了蜂窩結構自由振動特性。Hayes等[16]采用微極理論研究了正六角形蜂窩胞元的蜂窩結構在垂向簡諧力激勵下的動態變形。文獻[17.18]采用尺寸優化方法研究了內六角負泊松比蜂窩材料的結構參數對結構減振、抗沖性能的影響規律。對于蜂窩多孔材料在減振方面的工程應用研究仍存在不足，尤其是對于低頻段的減振效果不佳。

聲子晶體是指由彈性固體周期排列在另一種固體或流體介質中形成的一種新型功能材料。國內外對聲子晶體的研究主要圍繞晶體的聲學特性上，現有文獻較少涉及到結構的振動特性研究。此外，聲子晶體在理論研究領域受到了很多關注，但對于應用領域的研究較少。Pennec等[19]采用數值模擬的方法研究了周期性板中的局域共振型帶隙特性，并在試驗中進行了驗證;Diaz.De.Anda等[20]從理論的角度研究了聲子晶體中周期Timoshenko桿的彎曲振動帶隙，吳旭東等[21]提出了一種雙側振子布置形式的局域共振聲子晶體梁結構，并基于傳遞矩陣法和有限元法分析了雙帶隙配合減振的特性。對于聲子晶體的低頻減振特性，劉正猷等[22]提出了聲子晶體的局域共振的概念，為聲子晶體在低頻減振降噪領域的應用奠定了理論基礎。文獻[23.24]以梁框架結構低頻減振為目標，將質量放大局域共振聲子晶體嵌入框架結構中，對框架結構一階固有頻率進行聲子晶體結構優化設計，抑制了一階固有頻率處的振動。文獻[25.26]利用手性結構進行梯度設計，在低頻段實現了局域共振帶隙的拓寬。張佳龍等[27]提出一種正八邊形孔狀局域共振聲子晶體結構，在中低頻范圍內具有較好的隔聲特性;Lai等[28]和Mei等[29]基于局域共振機理設計了體和薄膜超材料，解決了低頻降噪減振的控制問題。利用局域共振型的聲子晶體結構能夠實現低頻減振的優點，文獻[30]中將聲子晶體結構的可設計性與負泊松比效應蜂窩基座局域剛度的可設計性相結合，提出一種聲子晶體負泊松比效應蜂窩基座，但對該基座的減振機理缺少深入分析。

本文在文獻[30]的基礎上進一步研究聲子晶體負泊松比效應蜂窩基座的減振機理，通過建立動力學模型探討聲子晶體結構參數對該基座減振性能的影響規律，提出低頻局域共振型聲子晶體負泊松比效應蜂窩基座設計的方法。

1 聲子晶體負泊松比效應蜂窩基座〖2〗1.1 負泊松比效應蜂窩基座? 本文采用文獻[30]中的負泊松比蜂窩基座模型，該負泊松比蜂窩基座結構如圖1所示，其由三部分組成：上面板、蜂窩芯、下面板，結構長400 mm，高300 mm，寬224 mm，共7層胞元，上下面板厚6 mm。胞元形狀為內凹等高度可閉合蜂窩胞元，壁厚、胞元內凹角分別為1 mm，-38.2°，基座上面板承載的設備質量為500 kg。

1.2 聲子晶體蜂窩基座的結構設計

在負泊松比效應蜂窩基座結構的基礎上，通過添加周期性分布的聲子晶體（由鉛塊與橡膠塊構成），設計聲子晶體負泊松比效應蜂窩基座。即以蜂窩基座的蜂窩單胞為基體，向單胞內填充橡膠和鉛塊，鉛塊作為散射體，橡膠作為彈性體，從而得到局域共振型聲子晶體負泊松比效應蜂窩基座，如圖2所示。

蜂窩胞元中聲子晶體結構的尺寸定義方式如圖3所示：蜂窩單胞寬度B、高度H、內凹角θ;散射體寬度b、散射體高度d;彈性體厚度h。基座采用鋼材制造，楊氏模量210 GPa，密度7800 kg/m3，泊松比0.3;橡膠的彈性模量為1 MPa，密度為1300 kg/m3;鉛塊的彈性模量為40.8 GPa，密度為11600 kg/m3。

聲子晶體負泊松比效應蜂窩基座的局域共振減振機理〖2〗2.1 聲子晶體負泊松比效應蜂窩基座的簡化動力學模型? 本文將聲子晶體負泊松比效應蜂窩基座簡化為圖4所示質點系振動系統。M，K分別為蜂窩基座的質量（設備質量與基座自身結構質量之和）和整體垂向剛度;F為外載荷激振力;x為蜂窩基座的垂向振動位移。設基座中有n個聲子晶體;mi，ki，ci，xi（i=1，2，…，n）分別表示第i個聲子晶體的質量、垂向剛度、阻尼系數和垂向振動位移響應。聲子晶體的質量為鉛塊和橡膠塊的質量之和，聲子晶體的剛度為橡膠塊的垂向剛度。

綜上，當聲子晶體與蜂窩基座的固有頻率接近（fp=fn）時，適當的配置阻尼材料，能夠有效抑制蜂窩基座在共振頻率點速度響應峰值，實現低頻減振。

2.3 聲子晶體負泊松比效應蜂窩基座的減振機理分析? 局域共振聲子晶體結構如圖3所示，由于閉合的剛性邊界和彈性介質的存在，基體中傳播的行波被共振單元局域化，平移局域共振模態被激發，基體可等效為剛性的邊界，等效模型如圖9所示。彈性波在聲子晶體結構中傳播，即等效為在圖9動力系統[31]中施加激振力F，當外載荷F的激振頻率與彈性體反饋力N的頻率相同時，兩作用力反向疊加，基體合外力為零，因而基體趨于靜止狀態，彈性波局域化，振動無法傳播，僅限于共振單元（散射體）中，由基體中傳播的彈性波被局域共振的散射體（鉛塊質量塊）吸收，導致該頻率的彈性波無法通過聲子晶體結構而傳播出去。

l通過上述理論和三類參數（γ，μ，ζ）計算分析表明：

（1） 通過在負泊松比蜂窩結構胞元內嵌入聲子晶體，有效抑制了低頻段的結構振動現象，從而實現了“小尺寸晶體控制大波長”。

（2） 在聲子晶體共振結構中，由于橡膠塊彈性體包覆層的存在，將較硬的鉛塊連接在基體上，組成了具有低頻的共振單元。當基體中傳播的彈性波的頻率接近共振單元的共振頻率時，共振結構單元將與彈性波發生強烈的耦合作用，使其不能繼續向前傳播，從而實現減振效果。

（3） 通過設計單個聲子晶體的動力學參數（質量、剛度、阻尼），可改變聲子晶體負泊松比效應蜂窩基座共振頻率附近的減振效果，即由單個聲子晶體的局域共振特性決定。

（4） 下文中分析的聲子晶體周期分布層數與減振效果的規律表明，隨著聲子晶體中彈性體填充率的增加（質量比的增大），聲子晶體基座的減振效果增強。

對于局域共振型聲子晶體，以上四條基本特征，是認定局域共振型聲子晶體時常用的判據。局域共振機理表明，彈性波激振頻率接近聲子晶體周期結構中散射體的固有頻率時，彈性波的能量大幅度的被散射體吸收，從而隔離了彈性波在聲子晶體周期結構中的傳播。因此，局域共振型聲子晶體周期結構的減振本質是利用散射體的局部共振現象吸收彈性波能量。本文設計的聲子晶體負泊松比蜂窩基座結構中，利用聲子晶體結構的局域共振特性，吸收由激振力引起的彈性波能量，降低傳遞到蜂窩基座的能量，從而減小蜂窩基座的響應。

3 局域共振型聲子晶體的減振優化設計? 基于上述減振機理分析，本文將設計一種局域共振型聲子晶體，通過優化方法設計聲子晶體固有頻率fp使其等于蜂窩基座固有頻率fn，之后分析該聲子晶體負泊松比蜂窩基座在共振頻率點的速度響應，驗證其減振性能。由于聲子晶體中存在橡膠材料，因此該聲子晶體蜂窩基座的阻尼特性比較復雜，為簡化優化過程，擬采用臨界阻尼忽略阻尼比對優化設計的影響。

3.1 聲子晶體負泊松比效應基座的減振性能評價方法? 為比較減振效果，對照文獻[30]中原蜂窩基座減振系統，本文建立聲子晶體負泊松比效應基座動力學模型，以便于分析添加聲子晶體后的聲子晶體負泊松比效應蜂窩基座的減振效果。

將該基座安裝在指定板架上形成減振系統（如圖10所示）。支撐板架長2000 mm，寬710 mm，板厚6 mm。板架縱骨采用T型材TN50×50×5×7，肋骨用等邊角鋼L20×3;板架及基座均采用楊氏模量210 GPa，密度7800 kg/m3，泊松比0.3的鋼材制造。基座上面板所承載的設備質量為500 kg，在基座上面板節點處均勻施加垂向簡諧激振力（振幅為20 N，10.500 Hz），板架的兩條短邊簡支，臨界阻尼系數取2%。

選取板架骨材上6個評價點的速度頻響幅值來評價基座減振效果，評價點的分布位置如圖11所示。

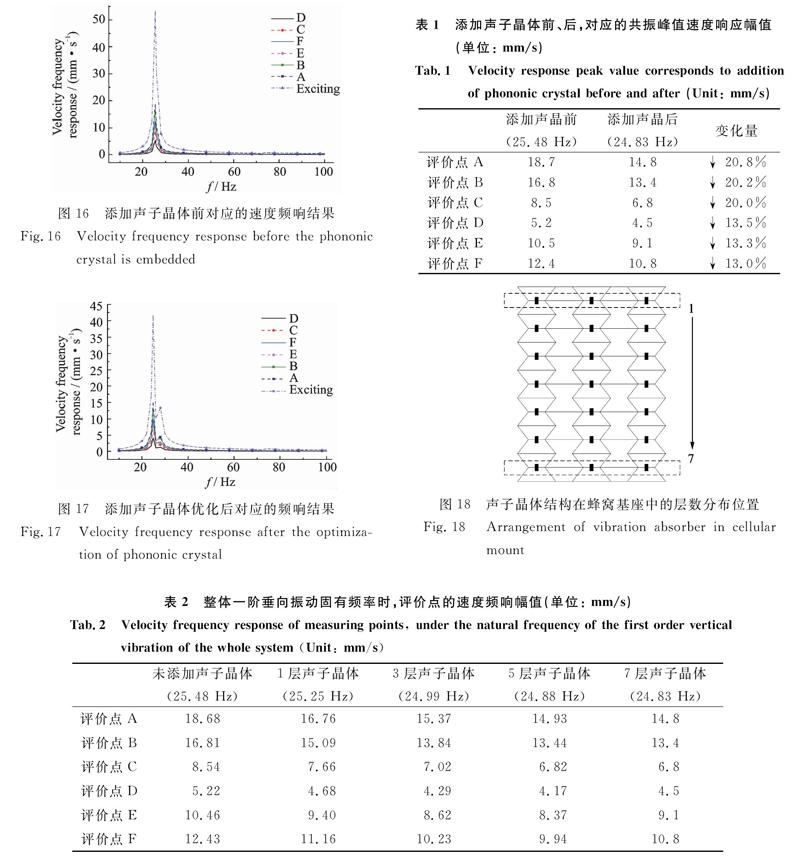
為評價該聲子晶體負泊松比效應基座的減振效果，分別計算了添加聲子晶體前/后結構的頻響結果，對速度響應共振峰值時對應的六個評價點振動幅值進行比較，添加聲子晶體前、后的速度頻響結果分別如圖16和17所示。表1中，添加聲子晶體前、后固有頻率分別為25.48 Hz和24.83 Hz，對應的評價點速度響應共振峰值進行了總結，各評價點的速度幅值降低了13.0%.20.8%（1.2.2.0 dB）。這表明該聲子晶體負泊松比蜂窩基座能夠有效抑制低頻共振現象，具有較好的低頻減振性能。

4 聲子晶體層數對減振性能影響規律

基于優化后的聲子晶體蜂窩基座，分析聲子晶體周期分布層數與減振效果的影響規律，按照由上而下的位置分布（如圖18所示），分別計算聲子晶體層數為1，3，5，7層時減振系統中各評價點的速度響應幅值，并提取對應的整體系統耦合一階垂向振動固有頻率點處的速度響應峰值（如表2所示）。表3總結了聲子晶體層數對應的減振系統速度頻響峰值變化率。

表2和3表明，添加聲子晶體后各評價點的速度頻響峰值得到有效控制，且隨著聲子晶體層數的增加，各評價點的速度頻響峰值趨于減小。說明該聲子晶體負泊松比效應蜂窩基座能夠有效抑制共振峰值。圖19總結了聲子晶體層數與速度頻響幅值減少量之間的關系，隨著聲子晶體層數的增加，基座的減振效果逐漸提升。

5 結 論

本文研究了聲子晶體負泊松比效應蜂窩基座的減振機理。建立簡化動力學模型以分析聲子晶體動力學參數對基座減振性能的影響規律，總結了減振機理，并分析聲子晶體層數與減振性能的關系。結論如下：

（1） 通過理論與計算分析，驗證了聲子晶體負泊松比效應蜂窩基座的低頻局域共振減振機理。

（2） 當聲子晶體固有頻率與蜂窩基座固有頻率接近時，能夠有效減小基座的共振響應峰值。

（3） 通過優化聲子晶體的固有頻率，能抑制蜂窩基座的共振現象，并保證整體結構的重量最小。

對于聲子晶體負泊松比效應基座的研究尚待實驗驗證，且對彈性體（橡膠）的阻尼效應也考慮不夠，后續研究將針對這些問題深入研究。

參考文獻：

[1] 楊鐵軍， 靳國永， 李玩幽， 等. 艦船動力裝置振動主動控制技術研究[J]. 艦船科學技術， 2006， 28（s2）：46.53.

Yang Tiejun， Jin Guo.yong， Li Wanyou， et al. Study on active control techniques for warship power plant[J]. Ship Science and Technology， 2006， 28（s2）：46.53.

[2] 呂林華， 楊德慶. 船舶鋼.復合材料組合基座減振設計方法分析[J]. 上海交通大學學報， 2012， 46（8）： 1196.1202.

Lv Linhua， Yang Deqing. Study on vibration reduction design of steel.composite materials hybrid mounting for ships[J]. Journal of Shanghai Jiaotong University， 2012， 46（8）： 1196.1202.

[3] 楊德慶， 謝小龍， 郭萬濤. 鋼.復合材料組合結構材料選型優化設計映射解法[J]. 應用力學學報， 2011， 28（01）： 29.34.

Yang Deqing， Xie Xiaolong， Guo Wantao. Mapping function method for hybrid steel.composite materials.structure selection optimization design[J]. Chinese Journal of Applied Mechanics， 2011， 28（01）： 29.34.

[4] 謝天宇， 王永生， 付 建， 等. 含阻尼層基座的加筋柱殼振動及聲輻射計算[J]. 武漢理工大學學報（交通科學與工程版）， 2013， 37（4）： 878.881.

Xie Tianyu， Wang Yongsheng， Fu Jian， et al. Computation of vibration and sound radiation from cylindrical shells with frame coated by damping layer[J]. Journal of Wuhan University of Technology（Transportation Science & Engineering）， 2013， 37（4）： 878.881.

[5] 計 方， 姚熊亮. 艦船高傳遞損失基座振動波傳遞特性[J]. 工程力學， 2011， 28（3）：240.244.

Ji Fang， Yao Xiongliang. The characteristics of vibration wave propagation from ship high transmission loss base structures[J]. Engineering Mechanics， 2011， 28（3）：240.244.

[6] 江國和， 薛 彬， 馮 偉，等. 艦用變壓器沖擊響應計算[J]. 噪聲與振動控制， 2010，29（3）： 108.112.

Jiang Guohe， Xue Bin， Feng Wei， et al. Ship transformer shock response calculation[J]. Noise and Vibration Control， 2010， 29（3）： 108.112.

[7] 張相聞， 楊德慶. 船用新型抗沖擊隔振蜂窩基座[J]. 振動與沖擊， 2015， 34（10）：40.45.

Zhang Xiang.wen， Yang De.qing. A novel marine impact resistance and vibration isolation cellular base[J]. Journal of Vibration and Shock， 2015， 34（10）： 40.45.

[8] Victor S， Tanchum W. On the feasibility of introducing auxetic behavior into thin.walled structures[J]. Acta Materialia， 2008， 57（1）： 125.135.

[9] 盧子興， 趙亞斌. 一種有負泊松比效應的二維多胞材料力學模型[J]. 北京航空航天大學學報， 2006， 32（5）：594.597.

Lu Zixing， Zhao Yabin. Mechanical model of two.dimensional cellular materials with negative Poissons ratio[J]. Journal of Beijing University of Aeronautics and Astronautics， 2006， 32（5）：594.597.

[10] Horrigan E J， Smith C W， Scarpa F L， et al. Simulated optimization of disordered structures with negative Poissons ratios[J]. Mechanics of Materials， 2013， 41（8）：919.927.

[11] Gibson L J， Ashby M F. Cellular solids： Structure and properties[M]. 2nd ed. Cambridge： Cambridge University Press， 1997.

[12] 李永強， 李 鋒， 何永亮. 四邊固支鋁基蜂窩夾層板彎曲自由振動分析[J]. 復合材料學報， 2011， 28（3）：210.216.

Li Yongqiang， Li Feng， He Yongliang. Flexural vibration analysis of honeycomb sandwich plate with complete clamped support[J]. Acta Materiae Compositae Sinica， 2011， 28（3）：210.216.

[13] 李永強， 李 潔， 李 鋒， 等. 四邊固支對稱蜂窩夾層板主共振非線性動力學計算[J]. 復合材料學報， 2012， 29（6）：179.186.

Li Yongqiang， Li Jie， Li Feng， et al. Primary resonance of the symmetric rectangular honeycomb sandwich panels with compleed damped supported boundaries[J]. Acta Materiae Compositae Sinica，2012， 29（6）：179.186.

[14] Hnig A， Stronge W J. In.plane dynamic crushing of honeycomb. Part I： Crush band initiation and wave trapping[J]. International Journal of Mechanical Sciences， 2002， 44（8）：1665.1696.

[15] Banerjee S， Bhaskar A. Free vibration of cellular structures using continuum modes[J]. Journal of Sound and Vibration， 2005， 287 （l.2）： 77.100.

[16] Hayes A M， Wang A J， Dempsey B M， et al. Mechanics of linear cellular alloys[J]. Mechanics of Materials， 2004， 36（8）： 691.713.

[17] Zhang X W， Yang D Q. Numerical and experimental studies of a light.weight auxetic cellular vibration isolation base[J]. Shock and Vibration， 2016， 2016（9）： 1.16.

[18] Zhang X， Yang D. Mechanical properties of auxetic cellular material consisting of re.entrant hexagonal honeycombs[J]. Materials， 2016， 9（11）：900.

[19] Pennec Y， Djafari.Rouhani B， Larabi H. et al. Low frequency gaps in a phononic crystal constituted of cylindrical dots deposited on a thin homogeneous plate[J]. Physical Review B， 2008， 78： 104105.

[20] Diaz.De.Anda A， Pimentel A， Flores J， et al. Locally periodic Timoshenko rod： Experiment and theory[J]. Journal of the Acoustical Society of America， 2005， 117（5）： 2814.2819.

[21] 吳旭東， 左曙光， 倪天心， 等. 并聯雙振子聲子晶體梁結構帶隙特性研究[J]. 振動工程學報， 2017，30（1）：79.85.

Wu Xu.dong， Zuo Shu.guang， Ni Tian.xin， et al. Study of the bandgap characteristics of a locally resonant phononic crystal beam with attached double oscillators in parallel[J]. Journal of Vibration Engineering， 2017， 30（1）：79.85.

[22] Liu Z， Zhang X， Mao Y， et al. Locally resonant sonic materials[J]. Science， 2000， 289（5485）： 1734.1736.

[23] Xiao Y， Mace B R， Wen J H， et al. Formation and coupling of band gaps in a locally resonant elastic system comprising a string with attached resonators[J]. Physics Letters A， 2011， 375（12）： 1485.1491.

[24] 張 印， 尹劍飛， 溫激鴻， 等.基于質量放大局域共振型聲子晶體的低頻減振設計[J].振動與沖擊， 2016， 35（17）： 26.32.

Zhang Yin， Yin Jianfei， Wen Jihong， et al. Low frequency vibration reduction design for inertial local resonance phononic crystals based on inertial amplification[J]. Journal of Vibration and Shock， 2016， 35（17）： 26.32.

[25] Baravelli E，Carrara M， Ruzzene M. High stiffness， high damping chiral metamaterial assemblies for low.frequency applications[C]. Health Monitoring of Structural & Biological Systems， International Society for Optics and Photonics，2013.

[26] Baravelli E， Ruzzene M. Internally resonating lattices for bandgap generation and low.frequency vibration control[J]. Journal of Sound & Vibration， 2013， 332（25）： 6562.6579.

[27] 張佳龍， 姚 宏， 杜 軍， 等. 基于局域共振型聲子晶體在機艙內低頻隔聲特性[J]. 硅酸鹽學報， 2016， 44（10）： 1440.1445.

Zhang Jialong， Yao Hong， Du Jun， et al. Low frequency sound insulation characteristics of the locally resonant phononic crystals in the large aircraft cabin[J]. Journal of Chinese Ceramic Society， 2016， 44（10）： 1440.1445.

[28] Lai Y， Wu Y， Sheng P， et al. Hybrid elastic solids[J]. Nature Materials， 2011， 10（8）： 620.624.

[29] Mei J， Ma G， Yang M， et al. Dark acoustic metamaterials as super absorbers for low.frequency sound[J]. Nature Communications， 2012， 3（3）： 756.762.

[30] 秦浩星， 楊德慶， 張相聞. 負泊松比聲學超材料基座的減振性能研究[J]. 振動工程學報， 2017， 30（6）： 1012.1021.

Qin Haoxing， Yang Deqing， Zhang Xiangwen. Vibration reduction of auxetic acoustic metamaterial mount[J]. Journal of Vibration Engineering， 2017， 30（6）： 1012.1021.

Abstract： In this paper， the local resonance reduction mechanism of phononic crystal cellular mount with auxetic effects is studied by establishing the dynamic model. The influence of the dynamic parameters （natural frequency ratio， mass ratio and damping ratio） on the vibration reduction performance of this mount is analyzed. It was shown that the frequency response of the cellular mount in the vicinity of the resonant frequency can be effectively reduced when the natural frequency of the phononic crystal is close to the natural frequency of the cellular mount. Then， the optimization design model of the phononic crystal auxetic cellular mount is established， and the phononic crystal structure with the specified local resonant frequency is obtained. The dynamic frequency response characteristics of this novel mount are calculated， which shows that the novel mount has better vibration reduction performance in low frequency resonance.

Key words： vibration reduction; phononic crystal; auxetic; cellular; mount

作者簡介： 秦浩星（1989.），男，博士生。電話：15821170061;E.mail：qinhaoxing@163.com

通訊作者： 楊德慶（1968.），男，教授，博士生導師。E.mail：yangdq@sjtu.edu.cn