高鐵線路重要部位WSN節點覆蓋算法設計

趙 凌

(鐵道警察學院 軌道交通安全保衛系， 鄭州 450053)

依照《鐵路安全管理條例》，高鐵線路應全線封閉管理，禁止無關人員入內。然而，不法分子往往通過翻越或破壞護欄，攀爬低矮路基、低矮橋墩或疏散通道等重要部位進入高鐵線路內部對相關設施或在建設備實施破壞、盜竊，危及列車行車安全及工程建設[1]。通常情況下，事發后不法分子已逃之夭夭，且高鐵線路多地處郊外，實施全線視頻監控成本較高、可行性尚需調研，這進一步加大了案件取證難度。

無線傳感器網絡(wireless sensor networks， WSN)的應用特點[2]為高鐵線路重要部位入侵報警提供了可行方案。然而，在高鐵線路重要部位大量部署傳感器節點會使得目標監測區域內的各節點通信覆蓋相互交叉，共享的無線信道干擾加劇，數據可靠傳輸受影響，導致節點因網絡冗余能耗開銷過大而提前“消亡”[3-4]。而監測盲區一旦形成將會給不法分子可乘之機。從近年的研究成果來看，文獻[5]提出了一種WSN節點覆蓋重疊最大有效覆蓋率的控制算法，對節點控制覆蓋進行了求解和驗證，并結合概率方法在一定程度上解決了節點冗余問題。文獻[6]為防止目標區域出現監測盲區，首先利用改進人工魚群算法對WSN節點進行了自適應定位尋優，再以此為基礎對節點分布模型進行優化，改善了節點覆蓋質量。文獻[7]在對WSN節點覆蓋漏洞分類的基礎上，提出了最小圓修補算法和蜂窩生長修補算法，提高了目標監測區域的節點覆蓋率。但上述算法對節點覆蓋質量缺乏明確的評價方法，對節點交叉覆蓋也缺乏直觀的優化依據。本文針對目標監測區域特點，使用二元感知模型[8]，基于遺傳算法[9]優化節點覆蓋率，同時盡可能減少工作節點數量。

1 高鐵線路重要部位與WSN節點感知模型

從人力防范和實體防范的角度，可將高鐵線路重要部位分為有人值守、無人值守和定期巡守3類，本文主要研究定期巡守的3種重要部位：低矮路基、低矮橋墩和在建高鐵建材設備所在地[1]。其入侵報警系統結構見圖1。

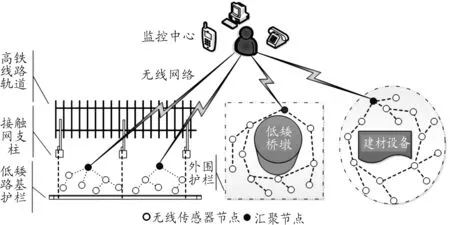
圖1 基于WSN的高鐵線路重要部位入侵報警系統結構

1.1 網絡模型

在環境條件比較惡劣的高鐵線路重要部位(低矮路基、低矮橋墩外圍護欄內側和在建高鐵建材設備附近)部署WSN節點實現入侵報警功能。假設網絡模型如下：

1) 將圖1中涉及的高鐵線路重要部位看作一個二維平面的目標監測區域，部署在該區域的WSN節點都由1個匯聚節點和大量分布于平面上的無線傳感器節點組成，每個節點都有全網唯一標識；

2) 所有節點一經部署不再移動；

3) 除匯聚節點外，其余節點能量有限；

4) 每個節點的位置信息是確定的；

5) 所有節點時間同步；

6) 節點周期性感知所在區域的入侵報警信號，借助已有的路由協議(如LEACH[10]或PEGASIS[11])經匯聚節點和無線網絡將信息傳至監控中心，實現實時預警。

1.2 提出問題

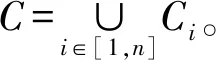
若監測區域中的每個目標節點至少被集合E中的一個節點感知覆蓋，僅當d(ei，ej)≤Rc時，認為集合E中各節點之間都至少存在一條通信路徑。各節點和通信路徑形成的網絡圖形為通信連通圖，集合E為目標監測區域的一個連通覆蓋集[12]。由此，本文研究的重點可轉化為：確定在二維平面上部署WSN節點時所形成的最優連通覆蓋集，即利用最少節點達到最大網絡覆蓋率。

1.3 WSN節點感知模型

節點的感知模型是節點覆蓋范圍和監測能力的決定性因素。從現有的文獻來看，節點感知模型一般分為3類：二元感知模型、概率感知模型和分段感知模型[13]。后兩種模型在一定概率的條件下可以轉化為簡單二元感知模型[14]。為方便分析計算，本文采用二元感知模型模擬節點的感知能力。

以二維平面作為目標監測對象，二元感知模型將傳感器節點抽象為1個以節點位置為圓心、以Rs為感知半徑的平面圓，Rs由節點本身的物理特性決定。

在二元感知模型下，若傳感器節點ei的坐標為(xi，yi)，對于監測區域內的任意目標點T(x，y)，ei與T(x，y)間的歐氏距離為

(1)

那么，當d(ei，T)≤Rs時，認為目標點T(x，y)被傳感器節點ei覆蓋。假設Pxy(ei)表示ei對T的感知概率，那么：

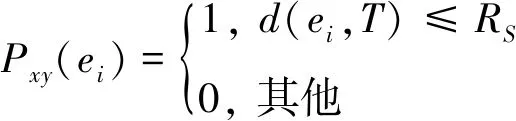
(2)

為進一步構建傳感器節點集合E={e1，e2，…ei，…，en}的感知模型，需引入隨機變量mi，i∈[1，n]，用于描述目標點T(x，y)被ei覆蓋，即mi：d(ei，T)≤Rs。令mi對應的概率為P{mi}，那么：

(3)

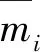
(4)

當ei與ej共同覆蓋目標點T(x，y)時，可用mi∪mj表示。若監測區域中各WSN節點相互獨立感知同一目標點，即各mi相互獨立，mi與mj是不相關的，i，j∈[1，n]，且i≠j，則有：

(5)

由式(5)可得，對于傳感器節點集合E，目標點T(x，y)被E覆蓋的概率即各mi對應概率的并集，可得該概率為

(6)

在二元感知模型下，若E中有1個節點覆蓋了目標點T(x，y)，則稱T(x，y)被E覆蓋；若E中沒有傳感器節點監測到T(x，y)，則稱T(x，y)未被E覆蓋。

將目標監測區域TA看作由l×k個像素點組成的離散區域，如圖2所示，每個像素點即傳感器節點要感知的目標點。設每個像素點的面積為Δx·Δy，據此可以計算出目標監測區域的總面積，記為ATA，則：

(7)

設E的區域覆蓋面積為AES，結合式(5)可得：

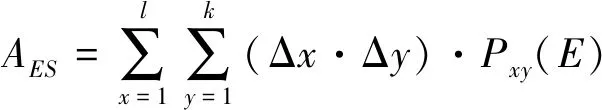
(8)

由此，傳感器節點集合E對目標監測區域的覆蓋率CR=AES/ATA為

(9)

1.4 WSN節點交叉覆蓋模型

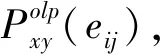
(10)

其中i，j∈[1，n]，且i≠j。由此可知，當目標點T(x，y)與傳感器節點ei和ej的距離都小于傳感器節點感知半徑Rs時，認為T(x，y)被ei和ej交叉覆蓋。若節點ei所覆蓋的區域已完全被其他節點覆蓋，此時ei可進入低功耗休眠狀態，不影響對整個目標監測區域的覆蓋。

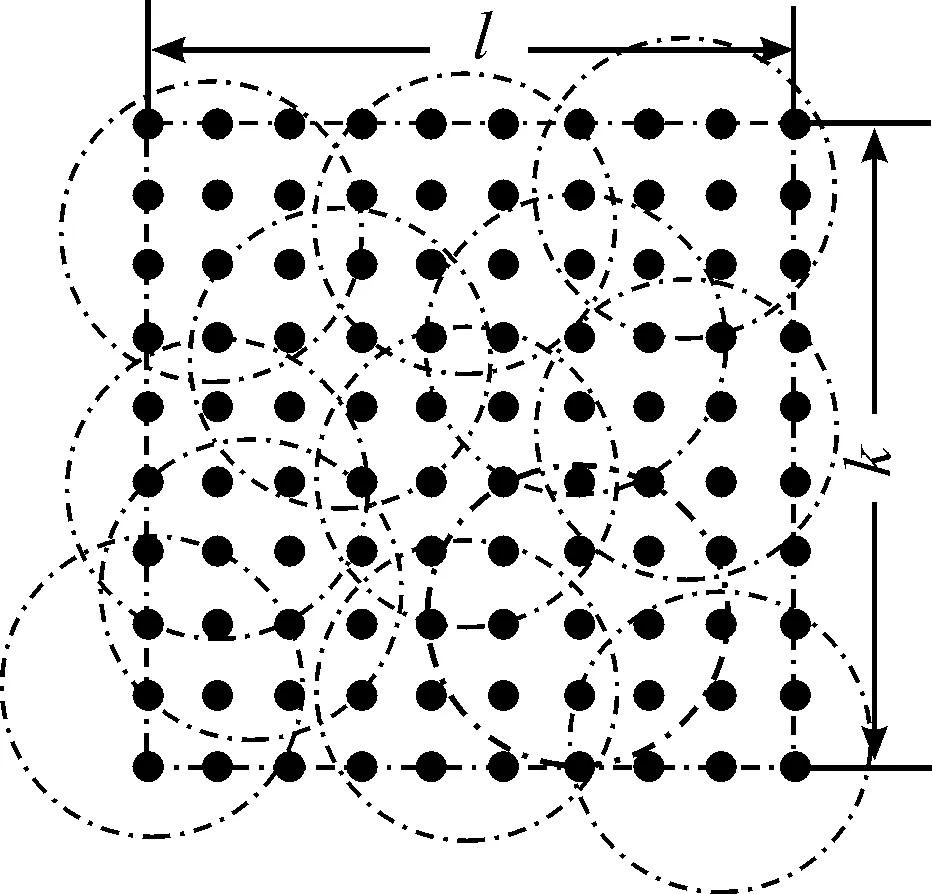
圖2 二元感知模型下的目標監測區域示意圖

2 基于遺傳算法的WSN節點覆蓋集優化算法設計

文獻[15]證明了節點集選取問題屬于NP完全問題[16]，遺傳算法按并行方式群體尋優，在解決NP問題方面優勢強大[17]，其運算流程如圖3所示。

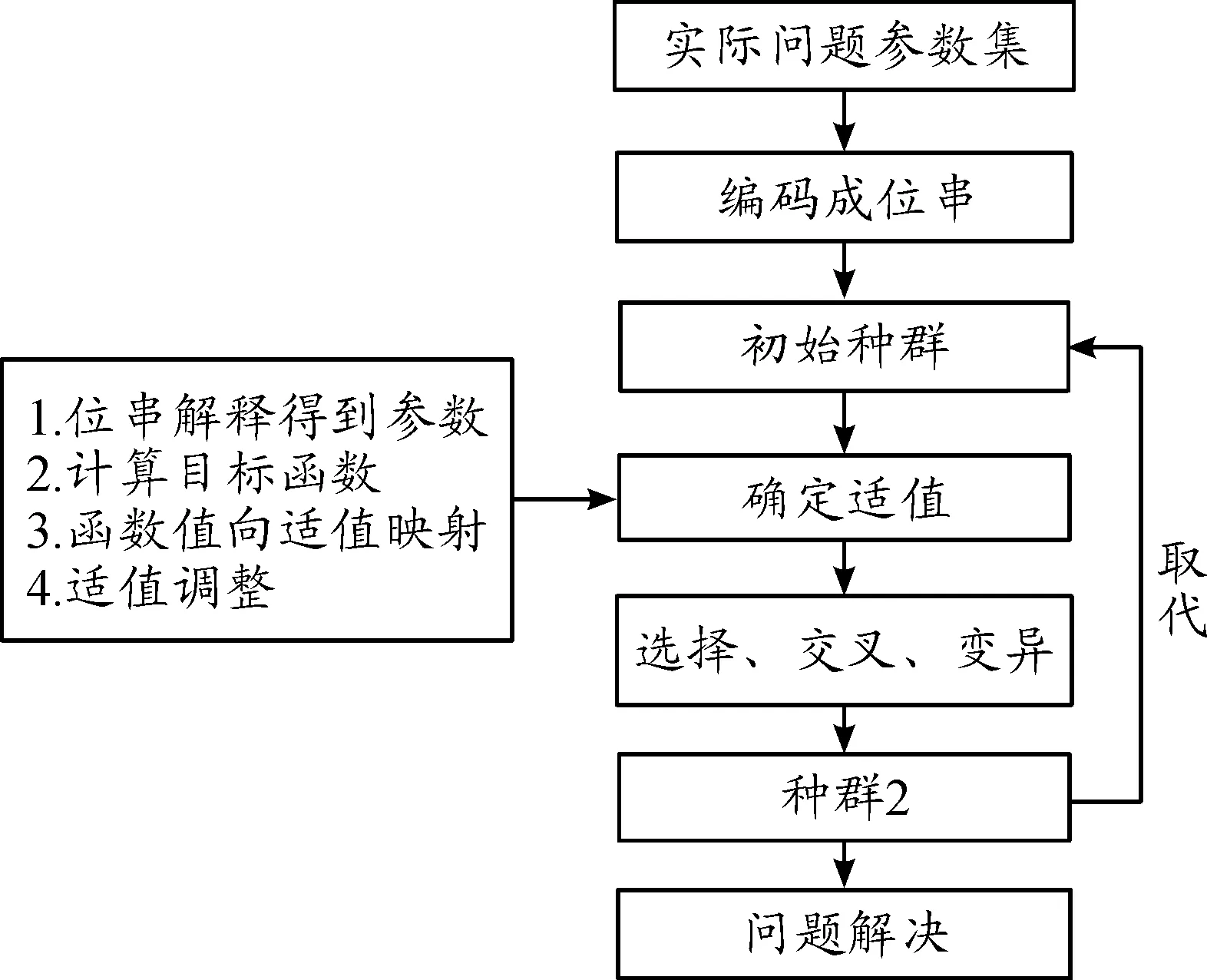
圖3 遺傳算法運算流程

2.1 編碼

節點覆蓋集選取的任務是從WSN節點集合中選擇一組覆蓋效果最優的節點工作，其余節點進入低功耗休眠狀態。采用位串bs={bs1，bs2，…bsi，…，bsn}將實際問題映射為對應的編碼參數集，即：

(11)

若目標監測區域部署10個WSN節點，則位串長度為10位。假設傳感器節點e2、e4、e6、e8、e10處于工作狀態，則此位串可表示為0101010101，如圖4所示。

圖4 編碼映射示意圖

2.2 建立初始種群

利用編碼映射建立1個由L個傳感器節點組成的初始種群，每個個體的染色體均由m個基因構成，初始化種群如式(12)所示。

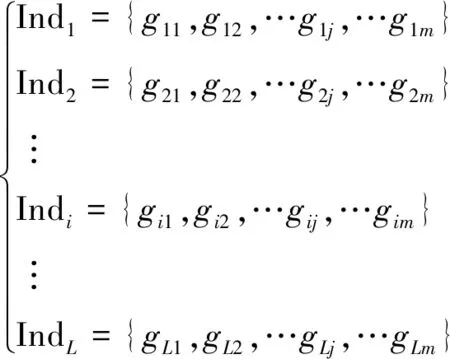
(12)

2.3 確定適值函數

文獻[18]中已經證明：當傳感器節點的無線通信半徑至少是其感知半徑的2倍，即當Rc≥2Rs時，在傳感器節點充分覆蓋目標監測區域的前提下，傳感器節點集合E總能保持連通性。

第1個目標函數是節點覆蓋率函數，設為f1(x)，由式(9)可知：

f1(x)=CR

(13)

第2個目標函數是工作節點數量函數，設為f2(x)，則有：

f1(x)=n′

(14)

其中n′為工作狀態節點數量。

由式(13)(14)可知，將f1(x)、f2(x)作為比值，比值越大，節點覆蓋率相對越高，同時節點數量就相對越少。如此，將多目標函數轉化為單目標函數。總目標優化函數設為fobt(x)，則有

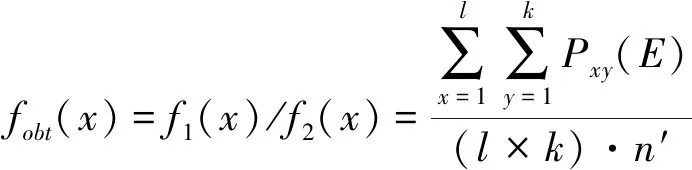
(15)

當fobt(x)值越大時，節點選取方案越優越。

2.4 選擇、交叉、變異、取代

選擇操作提高了遺傳算法的全局收斂性，常用的選擇算子有隨機聯賽法、隨機便利抽樣法和輪盤賭法[19]，本文采用輪盤賭法。傳感器節點個體被選擇的概率與其適值大小成正比，設個體被選擇的概率為Pcl，則

(16)

其中：wi是個體bsi的適值；K是種群規模。

交叉算子Pc決定了遺傳算法的全局搜索能力，本文采用單點交叉方式[20]實現交叉操作。若Pc值過大，個體更新過快，高適值個體會被快速破壞；反之，Pc值過小也會導致搜索停滯甚至算法不收斂，故Pc值一般取0.25～1。

變異算子Pm決定了遺傳算法的局部搜索能力，本文采用基本位交叉方式[17]實現交叉操作。若Pm值過大，很可能致使遺傳算法變為隨機算法；反之，Pm值過小將難以產生新的個體。一般Pm值取0.001～0.1。

當子代個體的適值大于父代時，發生取代操作。

2.5 局部搜索優化策略

在每一代取代操作發生之前，改變Indi的基因gij對應節點ej的工作狀態，即由1變為0，若此時的節點覆蓋率提高或保持不變，則保留0狀態；若節點覆蓋率下降則恢復節點為ej工作狀態[21]。遍歷所有基因，比較新舊染色體適應度值，若適應度值變大或不變，則保持修改，否則恢復修改。運行遺傳算法和局部搜索優化策略后得到新種群的適應度值至少大于等于原種群，進一步加速算法收斂過程。

3 仿真實驗分析

采用Matlab R2014a遺傳算法工具箱，對所設計的算法進行測試，在100 m×100 m的目標監測區域部署WSN節點。取種群大小為L=10，交叉算子Pc=0.75，變異算子Pm=0.05。

3.1 隨機部署節點覆蓋仿真

為驗證本文設計算法的優化效果，首先對隨機部署節點情況進行仿真。

隨機狀態下，設置節點覆蓋率>99%時，算法停止部署節點。由圖5可知，當節點感知半徑Rs=8 m時，所需節點數量為229；當Rs=14 m時，所需節點數量為116。即使感知半徑增加，所需工作節點總數有所減少，但節點交叉覆蓋依然突出。

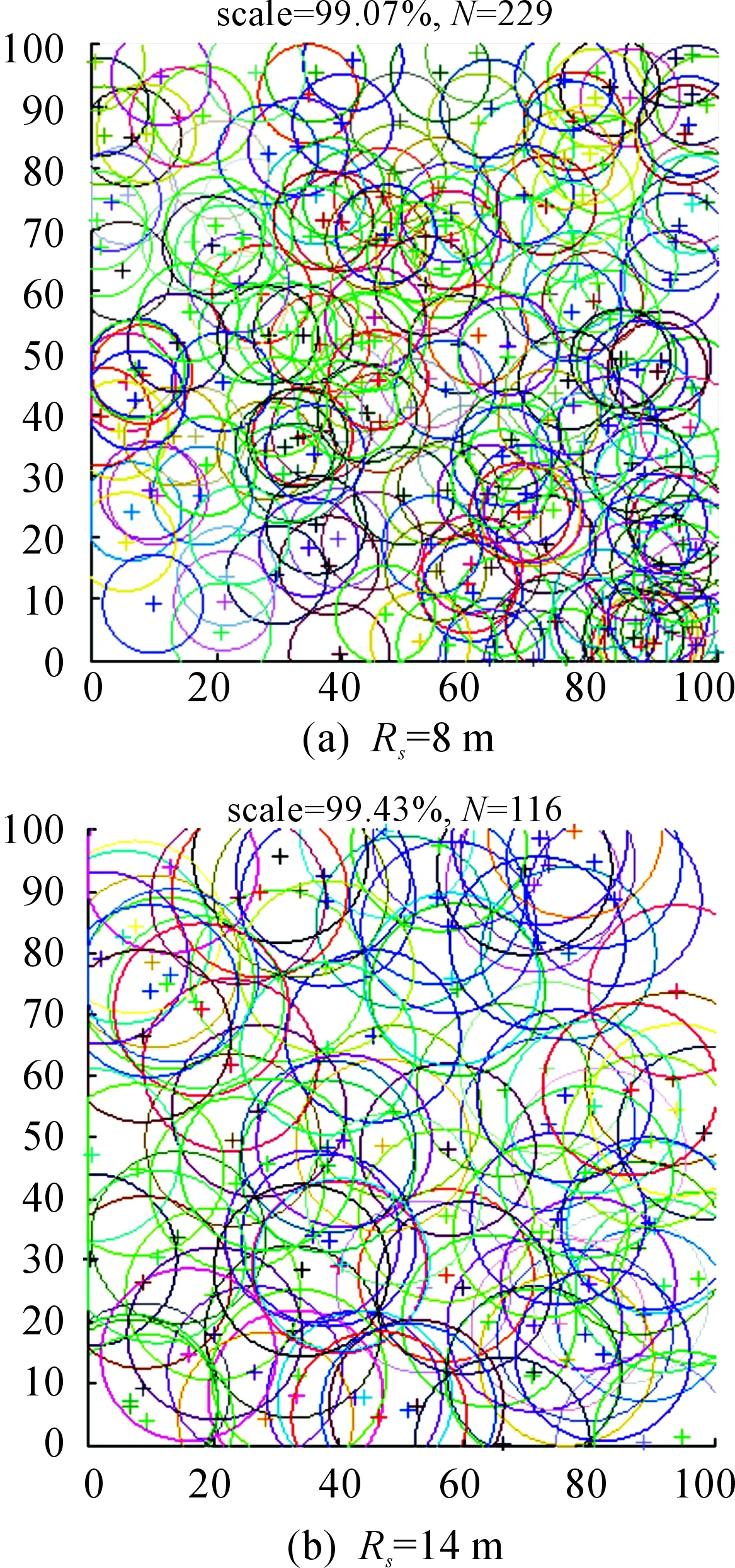
圖5 隨機部署節點

3.2 遺傳算法優化節點覆蓋仿真

為獲得最優連通覆蓋集，在仿真中考慮了高鐵線路防入侵精度及便于部署節點等因素，將節點的感知半徑設置為一個變化的區間，選取Rs∈[5，11]。算法從開始運行至100代期間，覆蓋率每變化1次，算法抓拍1次運行結果，順序抓拍結果如圖6所示。

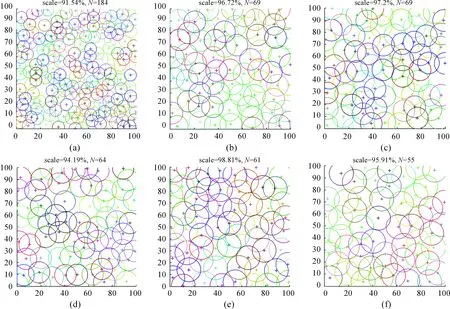
圖6 順序抽樣抓拍節點覆蓋情況

根據算法運行結果，圖6(a)～(f)所對應的總目標函數值如表1所示。

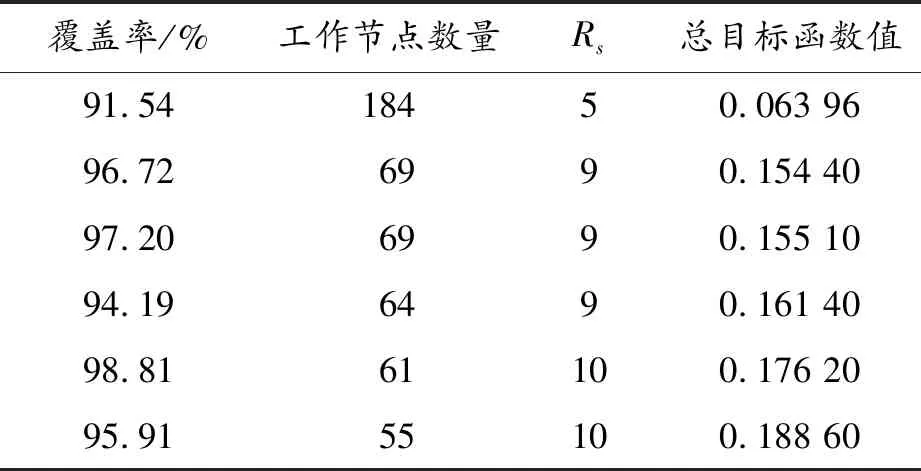
表1 順序抽樣總目標函數值對照表

由圖5和表1可知，算法在前100代運行期間，Rs由5增至10，節點覆蓋率整體變化趨勢不穩定，但工作節點數量逐漸變少。由此可見，隨著Rs的增大，工作節點數逐漸減少，總目標函數值逐漸變大，節點覆蓋集優化趨勢明顯。

為進一步驗證優化效果，令算法分別運行100、200、300和400代，得到節點覆蓋情況如圖7所示。

由圖7可知，隨著算法迭代次數的增加，節點覆蓋率由96.06%增至97.73%，工作節點數量為54，保持不變，算法優化成效顯著。根據算法運行結果，圖7(a)～(d)對應的總目標優化函數值如表2所示。

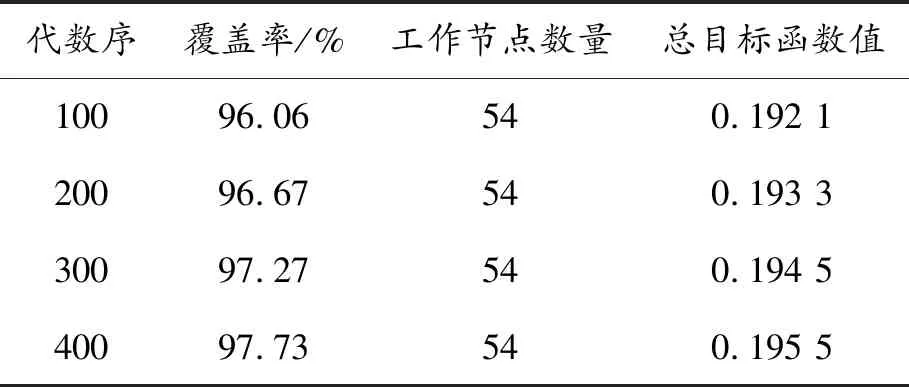
表2 算法運行結果統計

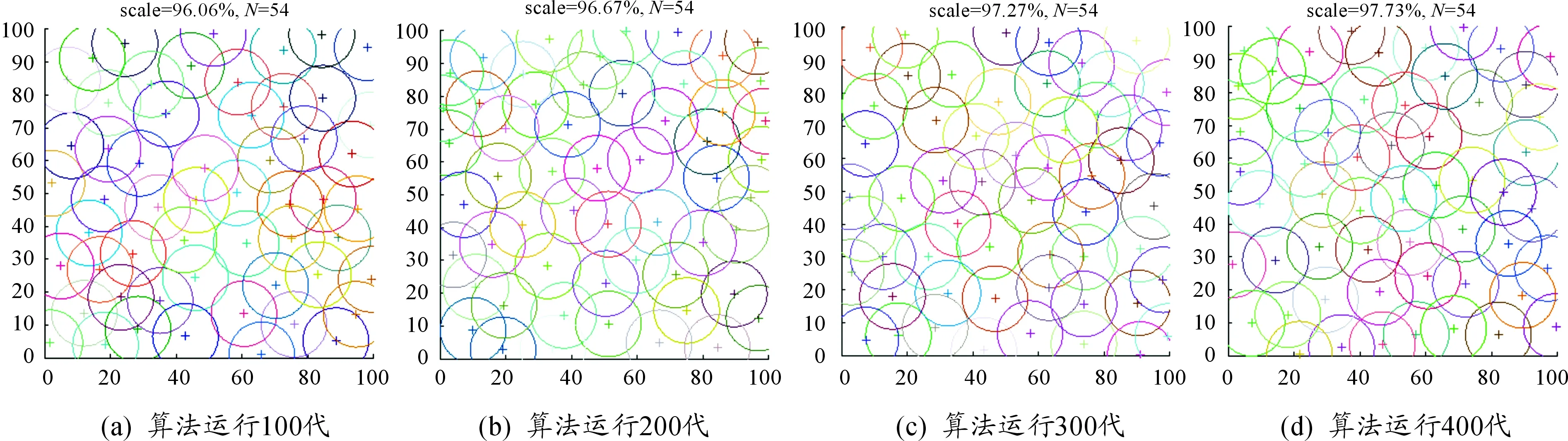
圖7 節點覆蓋集優化過程

顯然，算法運行至100代后，工作節點數量始終為54，輸出結果顯示此時的節點感知半徑Rs=10 m，如圖8所示。

圖8 算法運行400代時的結果

圖9給出了表2對應的總目標函數在算法運行400代期間的變化曲線。隨著迭代次數的增加，總目標函數變化曲線趨于直線，搜索向著全局最優解方向發展。由此可見，該節點覆蓋算法獲得了理想的覆蓋集選擇方案。

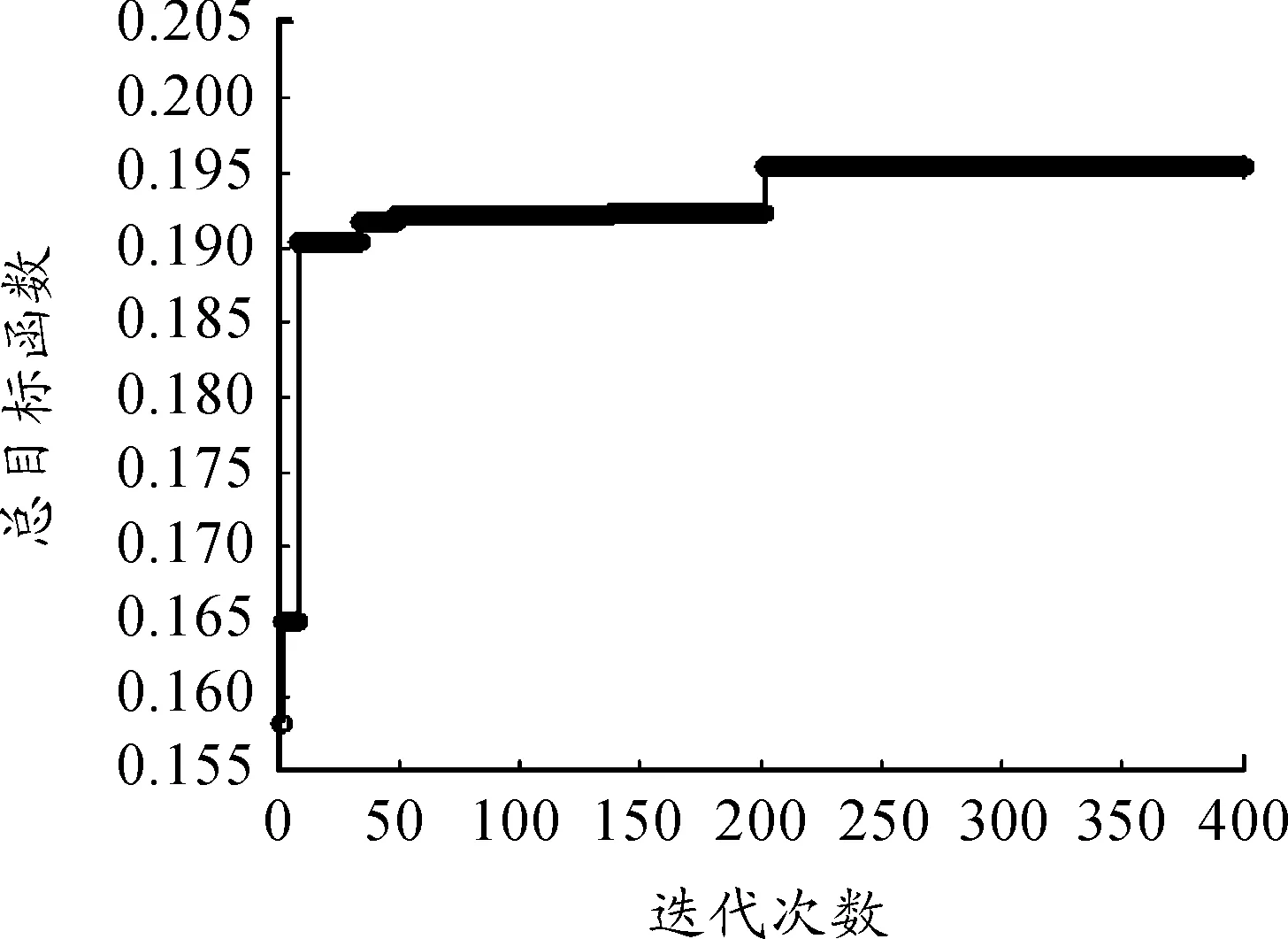
圖9 總目標函數變化曲線

為進一步驗證本文算法的先進性，進行節點覆蓋率對比。由圖10可知：在相同實驗環境和算法運行的迭代次數條件下，本文算法的節點覆蓋率大于遺傳算法，且隨著迭代次數的增加，本文算法要早于遺傳算法實現對目標監測區域的全覆蓋。由此可見，局部搜索優化策略進一步優化了節點覆蓋能力。

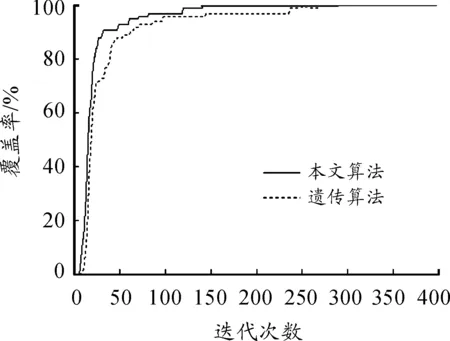
圖10 節點覆蓋率對比曲線

4 結束語

本文基于遺傳算法優化設計了WSN節點覆蓋集的高鐵線路重要部位入侵報警過程，為在二維平面區域科學合理地部署傳感器節點提供了參考。設計的節點覆蓋集優化算法同時減少了目標監測區域的節點交叉覆蓋和節點數量，與遺傳算法相比，優化了節點覆蓋能力。仿真結果表明：該算法具有良好的收斂特性，為下一步實地部署WSN節點、測試全網入侵報警功能提供了理論支撐。