淺埋黃土隧道圍巖壓力計算方法

于 麗，呂 城，段儒禹，王明年

(1.西南交通大學 土木工程學院，四川 成都 610031；2.西南交通大學 交通隧道工程教育部重點實驗室，四川 成都 610031)

淺埋隧道圍巖壓力的計算是確定隧道支護設計荷載的前提，國內外學者已通過數值計算[1-5]、理論分析[6-9]及模型試驗[10]等手段對淺埋隧道的破壞模式及圍巖壓力計算進行了研究，其中應用最為廣泛的主要為太沙基、謝家烋[6]、比爾鮑曼等理論計算公式或方法。太沙基理論假定土體為具有一定黏聚力的松散土體，從土壓力傳遞的角度出發研究了圍巖壓力，考慮了土體黏聚力、內摩擦角、埋深及隧道尺寸對圍巖壓力的作用；謝家烋[6]考慮淺埋隧道的破壞特征，基于極限平衡理論推導了圍巖壓力的計算方法，被鐵路和公路隧道規范采用；比爾鮑曼法是比較早的圍巖壓力計算方法，現在在實際中應用并不是很多。對于淺埋黃土隧道，根據現場調研情況[11-14]，黃土垂直節理普遍發育導致其破壞模式及圍巖壓力大小、分布不同于其他隧道，既有的圍巖壓力計算方法不能完全滿足工程實際情況，因此研究淺埋黃土隧道圍巖壓力的計算方法是十分重要的。

結合淺埋黃土隧道實際的破壞形式，構建淺埋黃土隧道的破壞模式，基于極限平衡理論，推導圍巖壓力的計算公式,并根據圍巖滑裂面上的應力狀態推導出圍巖破裂角的計算公式。并將本文方法計算的破裂角及圍巖壓力分別與現場實測值、既有方法的計算值進行對比，驗證本文破裂角及圍巖壓力計算方法的正確性和有效性，并分析不同參數對圍巖破裂角、圍巖壓力的影響。

1 圍巖壓力計算方法的建立

1.1 淺埋黃土隧道破壞模式

從隧道施工現場實際破壞情況來看，淺埋黃土隧道的坍塌面大多數為近乎直立的破裂面[14]，這是因為黃土垂直節理發育，在節理面上形成抗剪強度較小的軟弱面，當土體下方隧道施工形成臨空面時，受重力的作用，土體沿著垂直節理的軟弱面塌落。淺埋隧道施工后，上方地層形成滑動趨勢面，因黃土直立性好，在地表附近形成可見的裂縫[13]，據此建立淺埋黃土隧道的破壞模式如圖1所示。圖中：AA′和BB′均為垂直破裂面；A′C′和B′J′均為斜向破裂面，其與水平方向的夾角為β，β即為淺埋黃土隧道的破裂角；b為隧道半寬，m，b1為拱頂松動范圍的半寬，m；H為隧道高度；h為隧道上覆土體高度。

圖1 淺埋黃土隧道破壞模式

1.2 圍巖壓力理論推導

考慮隧道的對稱性，取隧道右邊一半進行受力分析，如圖2所示。圖中：W1為隧道拱部EBB′I的重力，kN；W2為肩部三角形土體JJ′B′的重力，kN；Pq為作用于隧道頂部的豎向圍巖壓力，kPa；Pe為水平圍巖壓力，kPa；λ為側壓力系數；T為直立破裂面AA′所受的切向摩擦阻力，kN；N為直立破裂面BB′所受的法向壓力，kN；T1為斜向破裂面A′C′所受的切向摩擦阻力，kN；N1為斜向破裂面B′J′所受的法向壓力，kN；F和F′為拱部土體EBB′I與三角形土體JJ′B′之間的作用力與反作用力，kN；X為中軸線上的靜止土壓力；c為土體的黏聚力，kPa；φ為內摩擦角，(°)；γ為土體的重度，kN·m-3。

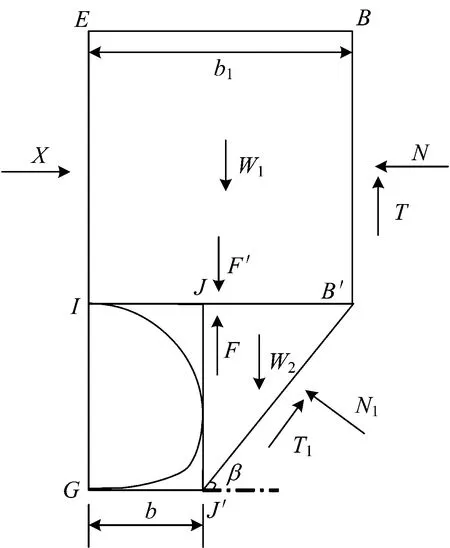
圖2 隧道受力分析圖

對于圖2所示的受力圖，根據受力平衡原理，建立如下土體的豎向和水平靜力平衡方程。

拱部土體EBB′F：

W1=Pqb1+T+F

(1)

X=N

(2)

三角形土體JJ′B′：

W2+F′=T1cosβ+N1sinβ

(3)

λPqH+T1sinβ=N1cosβ

(4)

土體EBB′J′GI：

Pqb1+T+T1sinβ+N1cosβ=W1+W2

(5)

N+N1sinβ-T1cosβ=X+λPqH

(6)

然后，在破裂面BB′和B′J′上分別應用Mohr-Coulomb強度破壞準，則有

T=ch+Ntanφ

(7)

(8)

由式(1)—式(6)可得到豎向圍巖壓力的計算公式為

(9)

又因為，拱部土體EBB′I的重力W1為

W1=γhb1

(10)

隧道拱部松動范圍的半寬b1為

(11)

隧道斷面矢跨比(扁平率)為

(12)

將式(10)—式(12)代入式(9)，并整理可得豎向圍巖壓力解析式為

(13)

水平圍巖壓力的計算公式為

Pe=λPq

(14)

對于黃土隧道深埋與淺埋的界定，即分界深度的取值，參照王明年[11]的研究成果，新黃土(Q3，Q4)的取上限55～60 m，老黃土(Q1，Q2)的取上限40～50 m。

2 圍巖破裂角理論計算公式

2.1 破裂角理論計算公式推導

由式(13)可知，對于具體的隧道，物理力學參數是確定的，僅需確定破裂角β。根據太沙基、朗肯土壓力的理論計算，松散體中的破裂角均為β=π/2+φ，對于這一計算式，易小明[15]給出了理論推導過程。但是，淺埋黃土隧道實際的破裂角明顯大于該公式的計算值，因此，根據圍巖滑裂面上的應力狀態推導其計算公式。

(2)黃土隧道常見的坍塌面為直立型，因此忽略陰影土體轉動對σ1的影響；

(3)隧道斷面的不規則形狀均簡化為矩形。

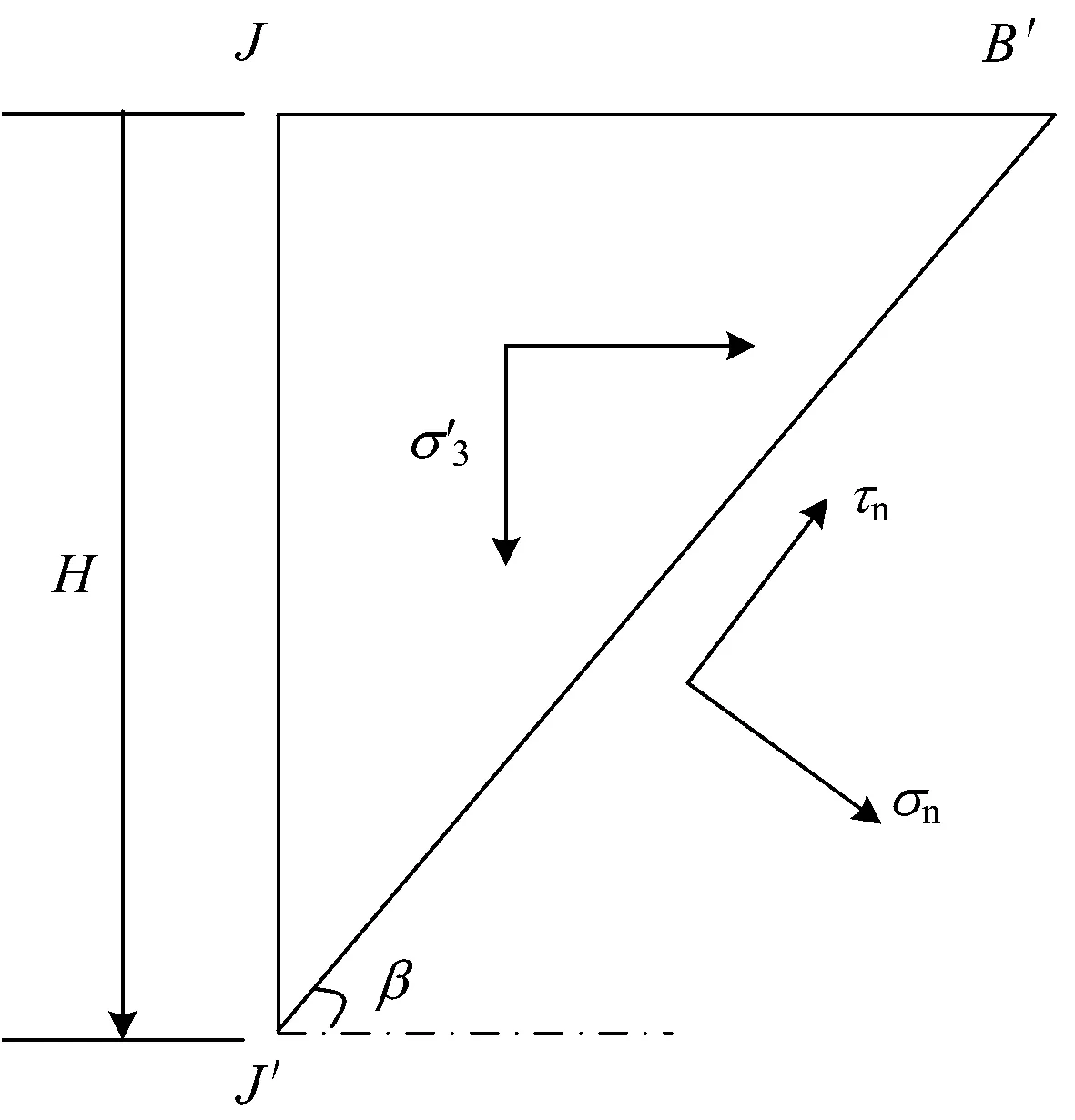
圖3 淺埋黃土隧道破裂角推導模型

將BB′IE土體的重力平均化，基于上述假設，等效得到附加應力作用下的右下側土體JJ′B′三角土體應力場為

(15)

(16)

且有，

(17)

式中：σ1和σ3為等效之前原巖的豎向應力、水平應力，kPa。

在滑裂面上任意一點原巖應力的關系為

(18)

而滑裂面上極限抗剪強度的極限為

τmax=σntanφ+c

(19)

令函數O(β)為滑裂面上極限抗剪強度函數與剪應力之差[6]，即

O(β)=τmax-τn

(20)

將式(17)—式(19)代入式(20)，并整理可得

(21)

當O(β)對β的一階導數為0時，隧道是最危險的。由此，對式(21)求導，并考慮K=H/2b，則得到隧道最危險時破裂角的計算公式為

(22)

2.2 破裂角計算方法對比

選取鄭西客專的賀家莊、呂家巖等6座黃土隧道，其物理力學參數及埋深均見表1。6座隧道的開挖高度和跨度相同，均為H=13.38 m，D=15.4 m(D=2b)。側壓力系數λ根據《鐵路隧道設計規范》計算，結果也見表1。土柱摩擦角θ取值根據《鐵路隧道設計規范》[16]選取平均值，Ⅳ級圍巖條件下取θ=0.9φc，Ⅴ級圍巖條件下取θ=0.7φc，結果也見表1。分別采用本文方法、謝家烋法、太沙基法(普氏理論與太沙基法相同)及易小明法，對6座隧道分別計算破裂角β，結果見表2；同時實測這6座隧道現場實際的破裂角β，并計算理論值與實測值的差值，結果均見表2。

表1 計算參數

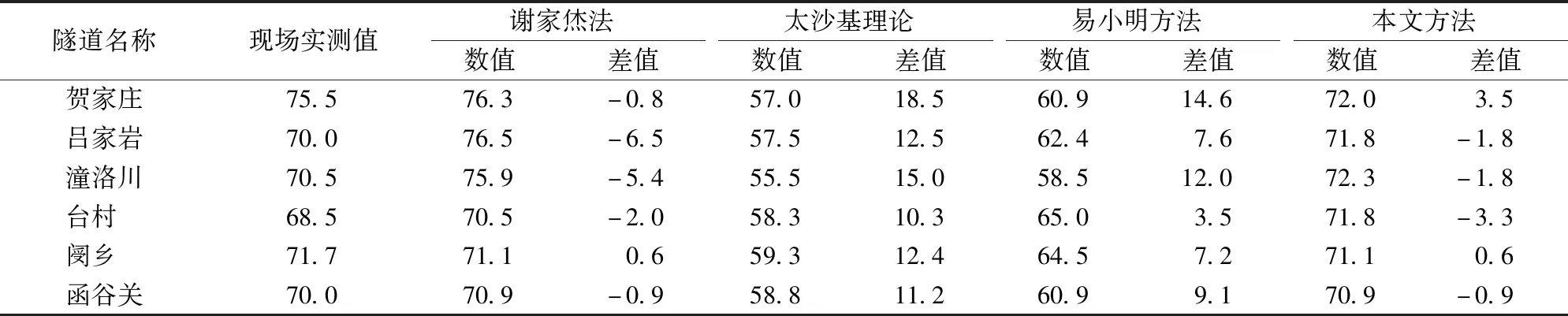
表2 破裂角β的計算結果驗證 (°)

從表2可知：謝家烋法計算的破裂角與實測值的差值為-6.5°～0.6°，本文方法與實測值的差值為-3.3°～3.5°，可見謝家烋法和本文方法與現場實測值均較接近，且本文方法的差值更小；同時，謝家烋法中土柱摩擦角θ取值對結果影響較大[17]，Ⅳ級圍巖條件下取θ=0.7φc～0.9φc，Ⅴ級圍巖條件下取θ=0.5φc～0.7φc，計算得到的破裂角相差分別達到7.7°和3.1°，并且這種取值方法完全憑借經驗，并無理論加以驗證，因此謝家烋法的結果受人為主觀因素較大。易小明方法得到破裂角的差值為3.5°～14.6°，太沙基理論的為10.3°～18.5°，兩者均遠大于本文方法的差值。

2.3 單一參數變化對破裂角的影響規律

以賀家莊隧道為例，單一參數變化時其值分別取：側壓力系數λ=0.4，0.5，…，1.5；內摩擦角φ=5°，10°，…，45°；斷面矢跨比(扁平率)K=0.5，0.6，…，1.5；隧道埋深h=10，15，…，50 m。分別采用本文方法、太沙基理論、易小明法及謝家烋法，分析這4個單一參數變化對破裂角β的影響，如圖4所示。

圖4 單一參數變化對破裂角的影響規律

從圖4可以得出如下結論。

(1)本文方法和謝家烋法計算的破裂角隨著側壓力系數的增大而緩慢的減小，即影響不是很明顯。太沙基法破裂角計算值與側壓力系數無關。易小明法的破裂角計算值在側壓力系數小于0.9時，破裂角隨著側壓力系數的增大而增大，增大的速率不斷增大；而在側壓力系數為1.0時破裂角突然減小；在側壓力系數大于1.0時破裂角計算值又隨著側壓力系數的增大而增大，增大的速率不斷減小。

(2)本文方法計算的破裂角隨著內摩擦角的增大而減小，而太沙基法、易小明法及謝家烋法計算的破裂角隨著內摩擦角增大而增大。現場調研的實際破裂角隨著內摩擦角的增大有減小的趨勢[11,13]。

(3)本文方法計算的破裂角隨著矢跨比的增大而增大，其他3種方法計算的破裂角變化不大。

(4)本文方法計算的破裂角隨著隧道埋深的增大而緩慢減小直到穩定；太沙基法和謝家烋法計算的破裂角與隧道埋深無關，易小明法計算的破裂角隨著隧道埋深的增大而明顯減小。

(5)綜合來看，本文方法計算的破裂角受影響最明顯的是矢跨比和內摩擦角。本文方法最符合淺埋黃土隧道的實際情況，驗證了本文方法的合理性及正確性。

3 圍巖壓力計算合理性驗證

選取賀家莊隧道、函谷關隧道及潼洛川隧道[4]，分別采用本文方法、太沙基法、謝家烋法和比爾鮑曼法計算淺埋黃土大斷面隧道圍巖壓力，并與現場實測值進行比較。3座隧道的物理力學參數取值仍見表1，開挖高度和跨度仍均為H=13.38 m，D=15.4 m(D=2b)。因現場調查監測圍巖壓力的位置與調查破裂角的位置并不是同一個地方，所以隧道埋深見表3。本文方法和太沙基法側壓力系數根據現場實測值進行選取，謝家烋法側壓力系數按照《鐵路隧道設計規范》相關公式進行計算，結果見表3。謝家烋法土柱摩擦角θ根據規范進行選取，Ⅳ級圍巖θ=0.8φc，Ⅴ級圍巖θ=0.6φc。圍巖壓力的現場實測值[13]和計算值見表3，計算值與實測值的差值見表4。

從表3、表4可知：對于豎向圍巖壓力，賀家莊隧道的太沙基法計算值小于現場實測值，這是因為太沙基法沒有考慮黏聚力的作用，據此進行支護設計是不安全的，可見太沙基法不能用于計算淺埋黃土隧道圍巖壓力；謝家烋法、比爾鮑曼法、太沙基法的另外2個隧道和本文方法的計算值均大于現場實測值，但本文方法的計算值與實測值更接近；對于水平圍巖壓力，謝家烋法、太沙基法、比爾鮑曼法的2個隧道均小于現場實測值，據此進行支護設計是不安全的；本文方法計算的豎向、水平圍巖壓力均大于現場實測值，具有一定的安全儲備，且豎向圍巖壓力明顯小于謝家烋法和比爾鮑曼法，因此本文方法計算淺埋黃土隧道的圍巖壓力是正確的、有效的。

表3 淺埋黃土隧道圍巖壓力計算結果

表4 不同計算方法圍巖壓力的計算值與實測值的差值

4 圍巖壓力計算值參數影響分析

這里只分析豎向圍巖壓力隨單一參數變化的規律。以賀家莊隧道為例，單一參數變化時其值分別取：側壓力系數λ=0.8，1.0，…，2.0；內摩擦角φ=15°，20°，…，45°；斷面矢跨比(扁平率)K=0.6，0.8，…，2.0，其中隧道開挖跨度D=15.4 m不變，高度取不同的值；隧道埋深h=15，20，…，45 m；黏聚力c=0,10，…，100 kPa；重度γ=15,17，…，21 kN·m-3。計算摩擦角φc=φ+10°，土柱摩擦角θ=0.7φc。分別采用本文方法、謝家烋法、太沙基法和比爾鮑曼法分析這6個單一參數變化對豎向圍巖壓力的影響規律，如圖5所示。由圖可得到如下結論。

(1)謝家烋法得到的側壓力系數一般小于1.0，而現有黃土隧道側壓力系數多分布在0.8～2.0之間[13]，所以不分析謝家烋法。隨著側壓力系數的增大，本文方法、太沙基法計算的圍巖壓力逐漸減小，而比爾鮑曼法的幾乎不變。

(2)隨著內摩擦角的增大，本文方法和謝家烋法計算的圍巖壓力均呈非線性減小，太沙基法呈線性減小，而比爾鮑曼法是先緩慢增大再緩慢減小。

(3)隨著矢跨比的增大，本文方法、太沙基法及比爾鮑曼法計算的圍巖壓力而逐漸增大，而謝家烋法的沒有變化，顯然謝家烋法忽略了矢跨比對圍巖壓力的作用，說明謝家烋法考慮不全面。

(4)隨著隧道埋深的增大，本文方法、太沙基法和比爾鮑曼法計算的圍巖壓力呈線性增大，謝家烋法先增大后減小。

(5)隨著黏聚力的增大，本文方法和太沙基法、比爾鮑曼法計算的圍巖壓力呈線性減小，謝家烋法無變化，說明謝家烋法的計算結果不符合實際規律。

(6)隨著重度的增大，4種方法計算得到的圍巖壓力均呈線性增大，增幅基本一致。

(7)綜上可知，本文方法的圍巖壓力計算值隨參數的變化符合一般規律，謝家烋法不能充分考慮黏聚力、矢跨比及側壓力系數的影響，太沙基法計算的圍巖壓力存在小于現場實測值的情況，比爾鮑曼法計算的圍巖壓力過大且不能體現側壓力系數對圍巖壓力的影響，可見，本文方法最能符合淺埋黃土隧道工程的實際情況，圍巖壓力計算值和現場實測值契合度高且具有一定的安全儲備。

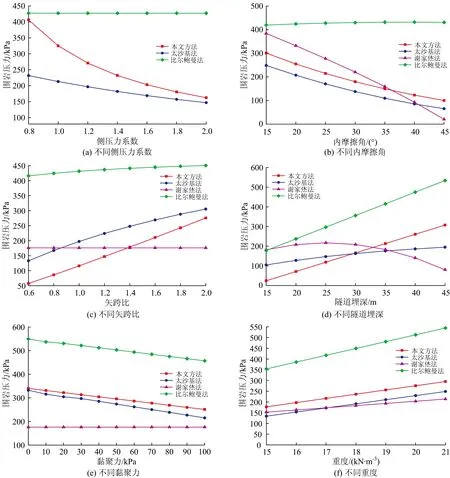
圖5 圍巖壓力隨參數的變化曲線

5 結 論

(1)本文結合現場實際破壞形式構建淺埋黃土隧道的破壞模式，基于極限平衡理論，推導出圍巖壓力的計算公式，并根據圍巖滑裂面上的應力狀態推導出圍巖破裂角的計算公式。

(2)對于圍巖破裂角，將本文計算方法以及既有的謝家烋法、太沙基法、易小明法的計算值均與實測值相比可知，謝家烋法的結果受人為主觀因素較大，太沙基法和易小明法均與實測值相差較大，本文方法與實測值最接近。本文計算方法認為，圍巖破裂角隨側壓力系數、內摩擦角和隧道埋深的增大而減小，隨矢跨比的增大而增大。

(3)對于圍巖壓力，將本文計算方法以及既有的謝家烋法、太沙基法、比爾鮑曼法的計算值均與實測值相比可知，本文方法的計算值與實測值更接近，且均大于現場實測值，具有一定的安全儲備。本文計算方法認為，圍巖壓力隨著側壓力系數、內摩擦角和黏聚力的增大而減小，隨著矢跨比、隧道埋深和土體重度的增大而逐漸增大。

(4)本文圍巖壓力和破裂角的計算方法克服了既有計算方法的不足，充分考慮了側壓力系數、內摩擦角、矢跨比、埋深、黏聚力及重度的影響，可為淺埋黃土隧道的設計提供理論依據。