重載鐵路隧道底部結構疲勞性能及累積損傷試驗研究

劉 聰，彭立敏，雷明鋒，劉 寧

(中南大學 土木工程學院，湖南 長沙 410075)

列車軸重的增大可大幅提升鐵路貨物運輸的能力和效率，降低單位貨物的運輸成本，美國、澳大利亞等國都在爭相發展本國的重載鐵路技術[1]。

然而，隨著軸重和時間的增長，重載鐵路隧道基底病害現象正日益凸顯[2]。大秦鐵路在經過二十多年的運營后，摩天嶺、軍都山等多座隧道產生了嚴重的、危及行車安全的基底病害，且基底病害多產生于重車線一側[3]，其中軍都山隧道基底下沉產生于基底中心和重車線側溝處，基底脫空最大高度達150 mm，引起上部軌枕最大位移達15 mm[4]。朔黃鐵路也有多座隧道產生了危及行車安全的基底病害，其中又以長梁山隧道最為嚴重，其重車線一側存在大量基底下沉及翻漿冒泥現象，最大沉降達15 mm，此外水泉灣隧道、大坪隧道等重車線一側基底病害也相當嚴重[3,5]。這些基底病害難以探查及處理，容易發展成危及行車安全的病害。

實測數據顯示，隧道底部結構的動力響應會隨軸重的提升而增大[6]，而受行車速度影響較小[7]，如21t軸重列車作用下，朔黃鐵路三家村隧道仰拱填充層表面最大豎向動應力為61.6 kPa[8]，25 t軸重列車作用下，豎向動應力最大為76.5 kPa[9]。

為探討重載鐵路隧道基底病害產生機理及底部結構疲勞性能，薛繼連[10]通過數值分析指出，當基底不密實，隧道底部仰拱填充的最大拉應力會激增，在30 t軸重列車作用下隧道底部結構將產生疲勞破壞。劉寧[11]通過疲勞試驗驗證了這一結論，其試驗結果表明，基底剛度越低，仰拱混凝土的疲勞損傷發展越迅速。ZHANG[12]通過數值分析指出，當基底存在空洞時，列車荷載引起隧道底部結構的位移及最大主應力將顯著增大，基于既有的混凝土受拉疲勞S—N曲線，其認為當空洞>2 m時，100年內隧道底部結構會產生疲勞破壞。

類似隧道疲勞性能的研究中，RICKSTAL[13]采用高速公路隧道實測車輛荷載進行了600萬次疲勞加載試驗，結果顯示其底板仍然完好。基于縮尺模型試驗，王祥秋[14]通過研究指出高速列車荷載作用下隧道底部結構不會產生疲勞破壞。

結構的疲勞性能既有試驗及數值分析主要側重于研究車輛荷載對隧道底部結構疲勞性能的影響，研究表明靜應力同樣會影響結構的疲勞性能[15]，但考慮圍壓壓力對隧道底部結構疲勞性能影響的研究較為少見，且圍巖壓力作用使隧道底部結構產生的靜應力遠大于列車荷載作用產生的動應力[16]。因此，本文針對隧道底部結構的受力特點，設計高靜載、低動載、雙側限彎拉室內疲勞試驗系統，開展軸重及圍巖壓力對重載鐵路隧道底部結構疲勞性能影響的試驗研究，揭示隧道基底病害的產生機理，為重載鐵路隧道基底結構維修養護提供科學依據。

1 疲勞試驗設計

1.1 隧道底部結構疲勞試驗系統

隧道中心處仰拱二次襯砌所受力為多向應力，該結構屬于有側限彈性地基梁受彎結構，將底部混凝土結構視為脆性材料，在典型圍巖、埋深、軸重條件下，施加靜載及循環動載，進行高靜載低動載條件下雙側限受彎疲勞試驗，由此設計的室內疲勞試驗系統如圖1所示。試驗箱體的長×寬×高為400 mm×300 mm×250 mm；在試件的前后左右采用側壓彈簧和數顯式千斤頂提供約束力，以模擬隧底結構所處的側限受力狀態；試件底部設置彈簧以模擬基巖與仰拱相互作用；試件頂部采用MTS疲勞試驗系統進行循環加載，以反映隧道底部結構高靜載低動載的受力特征。

圖1 疲勞試驗系統

試件采用的混凝土材料的質量配合比見表1。由靜力試驗得到150 mm立方體試件的抗壓強度為32.5 MPa，靜彈性模量為21.7 GPa；疲勞試驗采用100 mm×100 mm×300 mm的棱柱體試件，由無損檢測得到棱柱體試件動彈性模量為31.8 GPa，動泊松比為0.23；試件彎拉強度試驗表明，受拉區極限彎拉強度為2.5 MPa，破壞時對應峰值荷載為40.0 kN(均值)。

表1 混凝土材料質量配合比 kg·m-3

Ⅴ級圍巖彈性抗力系數為193.5 MPa·m-1，試件底部采用27個均布式彈簧模擬，單個等效彈簧剛度為215 kN·m-1。

1.2 循環加載及試驗工況

圍巖壓力為靜載，無列車運行時圍巖壓力單獨作用使結構產生靜應力σmin，圍巖壓力對應于最小疲勞荷載Fmin；列車荷載為動載ΔF，使結構產生動應力Δσ；當列車通過時，圍巖壓力Fmin與列車荷載ΔF共同作用使結構產生最大應力σmax，對應荷載為最大疲勞荷載Fmax。

試件的疲勞壽命受最大拉應力σmax、動應力Δσ及材料彎拉極限強度ft等多個因素的影響，因此引入變量應力/荷載水平S，以同時反映應力及彎拉極限強度對疲勞壽命的影響，并減少疲勞壽命公式中參數的數量。最小應力/靜載水平Smin、最大應力/荷載水平Smax、動應力/動載水平ΔS的定義如式(1)—式(3)所示。

(1)

(2)

(3)

式中：ft為彎拉極限強度；Ft為彎拉極限荷載。

試件受力特點如圖2(a)所示，通過液壓千斤頂施加側向力，采用MTS疲勞試驗機施加疲勞荷載，簡化后的等幅正弦波疲勞荷載如圖2(b)所示。

為研究動載、靜載對隧道底部結構疲勞性能的影響，建立的試驗工況見表2，其中動載工況下靜載為恒定值27 kN，靜載工況下動載為恒定值2.4 kN，各工況側向力均為1.5 kN。

1.3 傳感器布置

為測試應變和電導，在試件側面(非加載面)布置應變片和壓電陶瓷片，上、下側應變片分別位于跨中斷面頂部和底部，壓電陶瓷片位于跨中斷面中部。應變采用IMC動態應變儀記錄，電導采用PV80阻抗分析儀采集。以試件中部突然斷裂作為疲勞破壞的標志，同時以加載200萬次為控制次數。若試件破壞則終止試驗，記錄疲勞破壞時的加載次數；若試件未破壞而加載超過200萬次，則終止試驗。傳感器設置部位及試件破壞形態如圖3所示。

圖2 試件受力及疲勞荷載示意圖

表2 試驗工況

注：1—上側應變片；2—下側應變片；3—壓電陶瓷片

2 疲勞試驗結果

2.1 動載工況

動載工況下試件最大拉應變演化曲線如圖4所示。由圖可知：工況1(最大應力水平為0.65)時，試件在加載200萬次后仍未產生破壞，此時最大拉應變呈現2階段發展規律；工況2，3和4(最大應力水平≥0.70)時，最大拉應變呈現3階段發展規律，其演化曲線呈“倒S型”；試件疲勞壽命會隨著動載的增大而減小，試件疲勞破壞時最大拉應變為(282.1～295.8)×10-6。

圖4 動載工況下最大拉應變演化曲線

為準確描述動載工況下疲勞試件應變演化的3階段特征，構建統一的應變比演化曲線如圖5所示，曲線擬合公式見式(4)。式中：εn/ε0為試件加載N次后的最大拉應變εn與初始最大拉應變ε0之比；循環比N/Nf為試件已加載次數N與試件疲勞破壞時的加載次數Nf之比；λ，α，β，ρ為擬合參數。各工況擬合參數及其相關系數的值見表3。

(4)

圖5 動載工況下應變比演化曲線

表3 動載影響各工況擬合參數及其相關系數的值

由圖5可知：3階段試件的最大拉應變在第Ⅰ階段增長較快，第Ⅰ階段加載次數約為0.10Nf；第Ⅱ階段最大拉應變呈緩慢線性增長，其加載次數約為(0.80～0.85)Nf；第Ⅲ階段最大拉應變呈非線性增長，其加載次數約為(0.05～0.10)Nf。

2.2 靜載工況

靜載工況下試件最大拉應變演化曲線如圖6所示。由圖可知：工況5(最大應力水平為0.60)時，加載200萬次后仍未產生破壞，此時最大拉應變呈2階段發展；工況6—工況8(最大應力水平≥0.65)時，最大拉應變呈3階段發展；試件的疲勞壽命隨著靜載的增大而減小，試件疲勞破壞時的最大拉應變為(265.6～299.3)×10-6。

圖6 靜載工況下最大拉應變演化曲線

為準確描述靜載工況下疲勞試件應變演化的3階段特征，構建統一的應變比演化曲線如圖7所示，曲線擬合公式見式(5)，各工況擬合參數及其相關系數的值見表4。

圖7 靜載工況下應變比演化曲線

表4 靜載影響各工況擬合參數及其相關系數的值

由圖7可知：靜載工況3階段試件，其最大拉應變在第Ⅰ階段增長較快，第Ⅰ階段加載次數約為0.1Nf；第Ⅱ階段最大拉應變呈緩慢線性增長，其加載次數約為0.8Nf；第Ⅲ階段最大拉應變呈非線性加速增長，其加載次數約為0.1Nf。

2.3 2種型式試件的疲勞演化特征對比

選取工況5和工況7的應變及電導數據，對比分析2階段和3階段這2種破壞型式試件的最大拉應變增量、幅值與增速的疲勞演化特征。

2.3.1 最大拉應變增量

加載過程中維持荷載不變，隨著循環比的增加，試件的最大拉應變在不斷增大，表明試件內部的裂紋在不斷地擴展，其疲勞損傷在不斷地累積。最大拉應變增量的提高表明試件產生了不可恢復的內部損傷。定義最大拉應變增量為

(5)

工況5試件及工況7試件的最大拉應變增量隨循環比的演化關系如圖8所示。由圖可知：工況5試件的最大拉應變增量呈2階段發展，第Ⅰ階段最大拉應變增量增長迅速，第Ⅱ階段逐漸趨于平緩，以N/Nf=0.1為兩階段的分界點，此時最大拉應變增量約為30×10-6；工況7試件的最大拉應變增量呈3階段發展，第Ⅰ階段及第Ⅲ階段最大拉應變增量增速較快，第Ⅱ階段增長平緩，第Ⅰ與第Ⅱ階段分界點N/Nf=0.1處的最大拉應變增量約為42×10-6，第Ⅱ與第Ⅲ階段分界點N/Nf=0.9的最大拉應變增量約為120×10-6。

圖8 最大拉應變增量演化

2.3.2 最大拉應變幅值

荷載不變，試件的最大拉應變幅值也會隨循環比的增加(加載次數增大即循環比增大)而增大。定義最大拉應變幅值為

(6)

試件5及試件7的最大拉應變幅值隨循環比的演化關系如圖9所示。由圖可知：工況5試件最大拉應變幅值隨著循環比增加無顯著增大，加載過程中最大拉應變幅值為(12～14)×10-6；工況7試件的最大拉應變幅值隨循環比增加而增大，呈3階段發展，最大拉應變幅值為(30～63)×10-6。

圖9 最大拉應變幅值演化

2.3.3 最大拉應變增長速度

定義最大拉應變增長速度為

(7)

工況5試件及工況7試件的最大拉應變增長速度隨循環比的演化關系如圖10所示。由圖可知：工況5試件的最大拉應變增長速度非常小，趨近于0，表明在整個加載過程中最大拉應變始終穩定；工況7試件的最大拉應變增長速度呈3階段發展規律，第Ⅰ階段試件的最大拉應變增速較大，隨后逐漸減小，并在第Ⅱ階段(N/Nf∈(0.1,0.9))趨于定值，當N/Nf≥0.9，進入第Ⅲ階段后試件的最大拉應變增長速度迅速增大直至破壞。

圖10 最大拉應變增長速度演化

3 隧道底部結構疲勞性能及累積損傷

3.1 疲勞壽命

試驗所得動、靜載工況下試件疲勞壽命見表5。采用多元線性函數對表5中的數據進行擬合，得到試件在高靜載低動載環境下疲勞壽命N與最大應力水平Smax及動應力水平ΔS之間的關系見式(8)，相關系數R=0.92。當lgN=2時，表示試件所能承受循環加載次數為100萬次。本試驗中隧道仰拱結構試件的疲勞壽命遠大于4點彎折試件的疲勞壽命[17]。

lgN=-3.83Smax-13.57ΔS+5.68

0.60≤Smax≤0.80

(8)

表5 試件疲勞壽命

3.2 基于應變的非線性疲勞累積損傷

最大拉應變隨時間而產生的增量反映了混凝土內部損傷的演化。基于最大拉應變定義疲勞累積損傷D，即

(9)

圖11 基于應變的疲勞累積損傷演化

3階段試件基于應變的疲勞累積損傷演化擬合公式如式(10)，各工況擬合參數及其相關系數的值見表6；2階段試件基于應變的疲勞累積損傷演化擬合公式如式(11)，各工況擬合參數及其相關系數的值見表7。

(10)

(11)

表6 3階段試件基于應變的損傷演化各工況擬合參數及其相關系數的值

工況編號參數值αβ相關系數2-0.120.080.953-0.100.050.924-0.110.090.9660.02-0.160.977-0.120.080.958-0.190.190.83

表7 2階段試件基于應變的損傷演化各工況擬合參數及其相關系數的值

工況編號參數值abc相關系數10.07-0.571.060.9150.37-0.110.020.95

3.3 基于電導的非線性疲勞累積損傷

壓電陶瓷具有正逆壓電效應和機電耦合特性，結構損傷會引起壓電陶瓷的電導產生變化，為此測試壓電陶瓷電導的變化以表征試件在疲勞加載中的損傷演化規律。測試所得工況5試件的敏感頻段為120～280 kHz，工況7試件的敏感頻段為150～280 kHz，2種型式試件的電導演化曲線如圖12所示。由圖可知：隨著荷載循環次數的增加，電導曲線的峰值逐漸減小，諧振頻率逐漸增大，試件損傷在不斷加大。

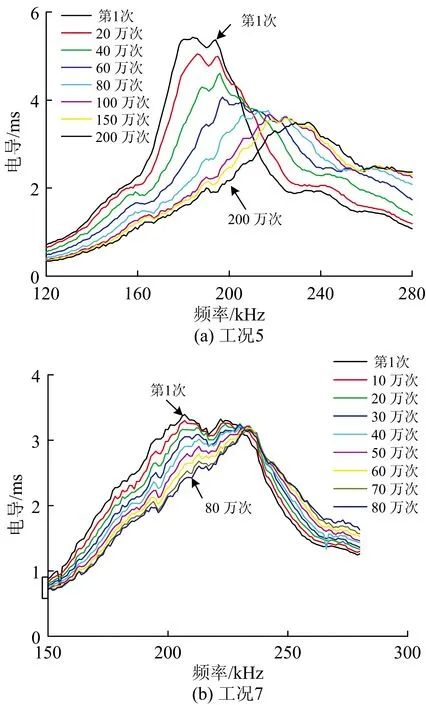
圖12 電導演化曲線

由測點3布置的壓電傳感器測得不同加載次數時試件的電導納數據，并取其電導數據由式(12)計算結構在不同循環次數下的疲勞累積損傷[18]。

(12)

式中：DRMS為試件累積損傷；Gm,0為初始狀態下頻率點m的電導基準值；Gm,i為不同損傷狀態下頻率點m的電導值。

基于式(12)所得到的疲勞累積損傷值大于1，經歸一化處理后，得到各工況試件疲勞累積損傷演化曲線如圖13所示。由圖可知： 2階段試件的損傷隨循環比增大而趨于平穩；3階段試件的損傷在第Ⅰ、第Ⅲ階段增長較快，N/Nf=0.1為第Ⅰ與Ⅱ階段的分界點，N/Nf=0.9為第Ⅱ與Ⅲ階段的分界點。

圖13 基于電導特性的疲勞累積損傷演化曲線

基于電導的3階段試件疲勞累積損傷演化擬合公式見式(10)，各工況擬合參數及其相關系數的值見表8； 基于電導的2階段試件疲勞累積損傷演化擬合公式見式(11)，各工況擬合參數及其相關系數的值見表9。

表8 基于電導的3階段試件損傷演化各工況擬合參數及其相關系數的值

工況編號參數值αβ相關系數2-0.140.060.953-0.130.040.944-0.140.060.976-0.140.060.957-0.120.040.938-0.180.090.96

表9 基于電導的2階段試件損傷演化各工況擬合參數及其相關系數的值

工況編號參數值abc相關系數10.36-0.02-0.050.9750.36-0.020.050.95

4 結 論

(1)當應力水平不大于0.6時，200萬次循環加載試件不會產生疲勞破壞，試件最大拉應變呈現2階段發展規律；當應力水平超過0.7時，試件最大拉應變呈“倒S”型3階段發展規律，并通過擬合得到了3階段試件最大拉應變的演化公式。

(2) 2種類型試件的應變演化存在顯著差異，2階段試件的最大拉應變及其增量在第Ⅰ階段增長較快，第Ⅱ階段趨于穩定，其最大拉應變幅值、增速始終保持恒定；3階段試件最大拉應變及其增量、幅值、增速在第Ⅰ、第Ⅲ階段增長較快，在第Ⅱ階段呈緩慢線性增長。

(3)試件的疲勞壽命隨靜載、動載的增大而減小；采用多元線性函數對試驗數據進行擬合，得到了高靜載低動載試件的雙參數疲勞壽命(S—N)計算公式；同時根據應變、電導的時變特性，分別構建了2階段及3階段試件的非線性疲勞累積損傷演化曲線及公式。