電制側向過岔時重載機車及車鉤的動態特性

張志超，李 谷，儲高峰，祖宏林

(中國鐵道科學研究院集團有限公司 機車車輛研究所，北京 100081)

鐵路道岔作為不同線路間的連接設備，因其結構復雜一直都是軌道的薄弱環節。重載列車側向通過道岔時會在輪軌之間產生復雜而劇烈的相互作用，引起明顯的輪軌橫向作用力和車鉤水平偏轉。而此時往往機車還需要施加電制動力控制重載列車進站速度，機車壓鉤力會隨著車鉤的大幅水平偏轉而產生明顯的橫向分力，該橫向分力通過機車一系和二系懸掛系統傳遞至輪軌界面，最終會加劇輪軌橫向相互作用，直接影響列車運行安全性和道岔使用壽命[1]，因此十分有必要對重載機車電制側向通過道岔時的動力學性能和車鉤動態特性開展深入的研究。

近些年，隨著我國重載列車長度和牽引噸位的不斷增加，重載機車車鉤緩沖器裝置(簡稱鉤緩裝置)的受壓穩定性及其對機車動力學性能的影響問題愈加明顯，科研人員對此投入了大量的研究力量并取得了卓有成效的研究成果[2-13]。中國鐵道科學研究院集團有限公司組織在大秦、神朔和朔黃、唐呼等重載線路開展了一系列的重載列車綜合試驗[2-5]，其中機車動力學測試主要監測了重載機車運行安全性指標及鉤緩裝置的運動形態，分析了車鉤偏轉角、縱向力大小與機車運行安全性的相互關系。張志超等[6-7]曾建立了重載機車扁銷鉤緩裝置的動力學分析模型，分析直線線路上鉤尾摩擦面狀態對鉤緩裝置受壓穩定性以及機車運行安全性的影響。EI-SIBAIE[8]在鉤緩系統建模時將1對連掛車鉤簡化為1根直桿，并考慮了鉤體的轉角。馬衛華等[9]和吳慶[10]建立了13A/QKX100型和DFC-E100型鉤緩裝置的動力學分析模型，著重分析了這2類鉤緩裝置系統特性對重載機車動力學性能的影響。許自強[11]通過數值仿真計算研究了既有重載機車采用的13A型和102型鉤緩裝置對33t軸重機車的適應性。許期英等[12]采用SIMPACK軟件反演得到車鉤鉤頭輪廓曲線，通過動力學仿真計算分析重載機車通過曲線時車鉤的偏轉行為。這些研究工作主要集中在直線線路上重載機車及其鉤緩裝置的運行安全性和受壓穩定性，曲線線路的相關問題較少涉及[11-12]，而對電制側向過岔重載機車及車鉤動態特性的研究更是少之甚少。

本文一方面理論推導了曲線線路上受壓連掛車鉤準靜態水平轉角的計算公式，分析準靜態車鉤轉角隨曲線半徑的變化規律；另一方面在前期研究成果[6-7]的基礎上，采用SIMPACK軟件建立了重載機車動力學模型和包括鉤尾“曲面—曲面”接觸摩擦單元、非線性遲滯特性緩沖器單元和扁銷止擋單元的鉤緩裝置動力學模型，通過子結構方法搭建了雙機重聯牽引的重載列車動力學模型。同時將道岔側向線路簡化為不考慮轉轍區和轍岔區鋼軌型面變化的S形曲線。在驗證模型正確性后，仿真計算了重載列車側向通過我國重載鐵路仍較為常見的12號道岔的機車動力學響應和車鉤動態偏轉，與準靜態車鉤轉角對比分析的同時，深入研究機車電制級位和車鉤鉤尾弧面摩擦系數等因素的影響規律。

1 曲線線路上受壓連掛車鉤準靜態轉角計算

依據標準TB/T 3334—2013《機車車鉤緩沖裝置》[13]的規定，機車鉤緩裝置按照結構形式分為100型、101型、102型和輕型。目前，我國重載機車大都采用100型鉤緩裝置。它的主要結構特點：車鉤鉤尾具有凸形圓弧面，能夠與前從板凹形圓弧面形成圓弧接觸摩擦副，提供車鉤受壓穩鉤力矩；車鉤與鉤尾框采用橢圓形扁銷連接，在車鉤偏轉角較大時通過扁銷與鉤尾框梨形孔的配合實現止檔作用。該鉤緩裝置鉤尾圓弧面接觸摩擦作用對車鉤受壓穩定性和重載機車運行安全性具有至關重要的作用[7]。

一般重載列車側向通過道岔時速度較低，可以不考慮道岔轉轍區和轍岔區鋼軌型面變化帶來的沖擊效應，僅考慮岔區線路曲線變化的影響(將其簡化為具有相同線路線形的S形曲線)后，可通過幾何關系計算推導曲線線路上受壓連掛機車車鉤準靜態轉角的計算公式。

通常認為，理想狀態下機車運行于曲線線路上時，機車前后車鉤沿著曲線中心線切線方向呈“八”字形分布，輪軌導向力的作用使得轉向架導向輪對貼靠曲線外軌，而非導向輪對貼靠曲線內軌。假設前后轉向架中心依然處于曲線中心線上，根據幾何關系推導可以得到連掛機車曲線通過時車鉤靜態轉角的計算結果[12-13]。但是，此車鉤靜態轉角僅是機車曲線通過時車鉤的最小自由轉角，并未考慮縱向車鉤力作用。如果機車在曲線線路上運行同時承受縱向壓鉤力作用，機車與車鉤的運動狀態會有很大變化。此時，壓鉤力的作用勢必使具有弧面鉤尾結構的兩連掛車鉤相對各自車體產生相反方向的水平偏轉，單節機車前后車鉤會呈“之”字形分布，如圖1所示，圖中：Lb為機車車體中心點至轉向架中心點的縱向距離；Lc為機車車體中心點至車鉤鉤尾的縱向距離；Lg為2個連掛車鉤總長度；v為車速。

圖1 曲線線路上受壓連掛機車及車鉤位置狀態

連掛機車曲線線路上受壓鉤力作用時車鉤轉角計算分析圖如圖2所示。

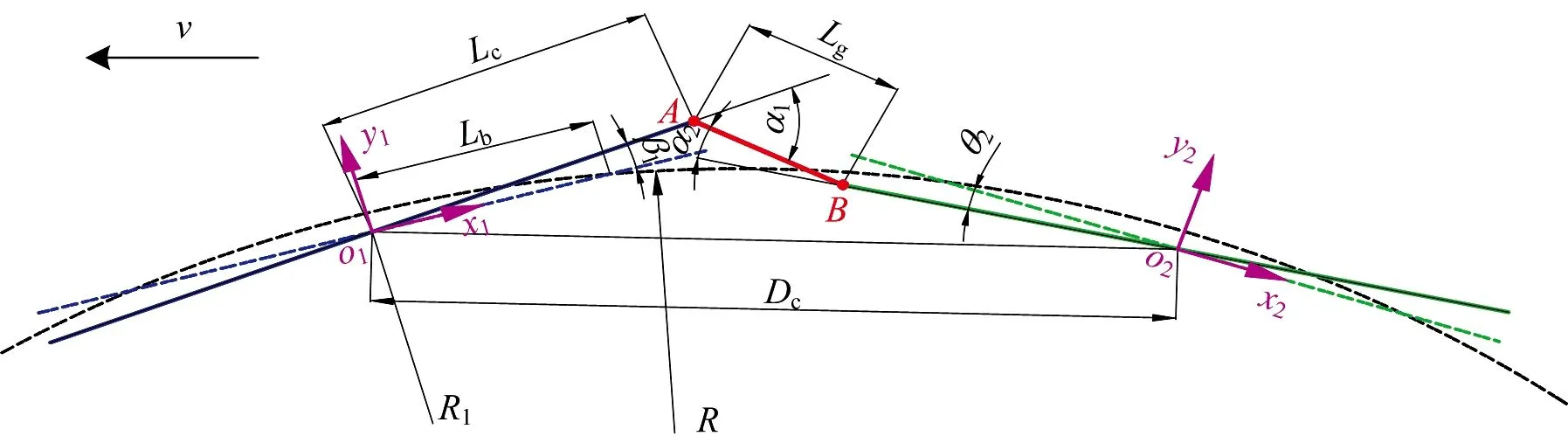
圖2 連掛機車曲線線路上受壓時車鉤轉角計算分析圖

依然假設機車前后轉向架中心都處于曲線中心線上，點O1和O2分別為2節連掛機車車體中心點，分別以這2個點為原點、以沿車體縱向中心線方向為x軸建立坐標系O1X1Y1和O2X2Y2。點A和點B分別為連掛車鉤兩端連接點，2個連掛車鉤中的前鉤和后鉤相對于各自車體的轉角分別為α1和α2。根據圖2所示幾何關系，2個車體中心點O1和O2所處曲線半徑R1要小于線路曲線半徑R，即

(1)

近似認為點O1和O2之間弧長s為

s≈2Lc+Lg

(2)

由式(1)和式(2)可以得到2車體中心點O1和O2間的圓弧角θ，也即坐標系O1X1Y1和O2X2Y2間相對轉動角度為

(3)

壓鉤力的作用會使得2機車車體分別繞其中心產生搖頭偏轉直至二系橫向止檔發揮作用，設dmax為機車二系橫向止擋最大間隙，包括自由間隙d和彈性壓縮量d1兩部分，則連掛機車車體搖頭偏轉角θ1和θ2分別為

(4)

當車體未發生搖頭偏轉時，車鉤上點A和點B在坐標系O1X1Y1和O2X2Y2中的坐標分別為

(5)

(6)

而當受壓狀態下的車體產生搖頭偏轉角θ1和θ2時，車鉤上點A和點B在坐標系O1X1Y1和O2X2Y2中的坐標變換為

(7)

(8)

幾何關系分析可知，坐標系O2X2Y2相對于坐標系O1X1Y1轉動了角度θ和平移了距離Dc，根據坐標系變換關系可以得到坐標系O2X2Y2中的點B在坐標系O1X1Y1中的坐標為

(9)

其中，

則連掛車鉤AB與坐標軸O1X1的夾角α為

(10)

前鉤和后鉤相對于各自車體的轉角α1和α2分別為

α1=α+θ1

(11)

α2=α+θ2-θ

(12)

某現役重載電力機車計算參數為Lc=17.652 m，Lb=10.06 m，Lg=10.06 m和dmax=0.03 m，根據式(11)和式(12)可計算2臺連掛機車受壓狀態下通過不同半徑曲線線路時的車鉤轉角見表1。

表1 曲線線路上受壓連掛機車車鉤轉角靜態計算結果

由表1可見：車鉤轉角隨著曲線半徑的減小而逐漸增大，并且前鉤轉角始終大于后鉤轉角，當曲線半徑為350 m時，前鉤和后鉤轉角分別為5.54°和4.86°。

2 重載列車側向過岔動力學模型

為了分析電制側向過岔時重載機車及車鉤的動態特性，借助多體動力學分析SIMPACK軟件，采用子結構方法建立雙機重聯牽引重載列車動力學模型，主要包括單節機車子結構、鉤緩裝置子結構和貨列簡化子結構3個部分，其中貨列子結構為將貨車部分簡化成只具有縱向自由度的1個虛擬貨車。

2.1 單節機車子結構模型

單節機車可簡化為由車體、構架、輪對、驅動單元等質量體和彈簧、阻尼元件構成的多剛體動力學模型。一系懸掛剛度由軸箱彈簧提供的垂向、橫向和縱向3個方向剛度及由軸箱定位裝置提供的定位剛度組合而成，一系懸掛垂向阻尼則由一系垂向減振器提供；二系懸掛剛度主要包括彈簧(或橡膠堆)提供的3個方向剛度及橫向止檔剛度、搖頭止檔剛度，二系懸掛垂向、橫向阻尼則由垂向、橫向減振器提供；電機懸掛剛度包括由電機吊桿及兩端橡膠關節提供的6個方向剛度。單節機車動力學模型共計52個運動自由度，如圖3所示。

圖3 單節機車動力學模型

2.2 鉤緩裝置子結構模型

鉤緩裝置動力學模型如圖4所示，該模型不考慮兩連掛車鉤鉤頭之間相對水平轉角，將其假設為1根直桿；從板通過緩沖器與車體相連接且僅具有縱向自由度，車鉤鉤體與從板之間建立“曲面—曲面”接觸摩擦單元，相對從板具有橫向、縱向和繞垂向軸轉動3個自由度；同時在鉤尾銷位置加入模擬扁銷止擋特性的單元。鉤緩裝置子結構主要包括鉤尾“曲面—曲面”接觸摩擦單元、非線性遲滯緩沖器單元和扁銷止擋單元等[6-7]。

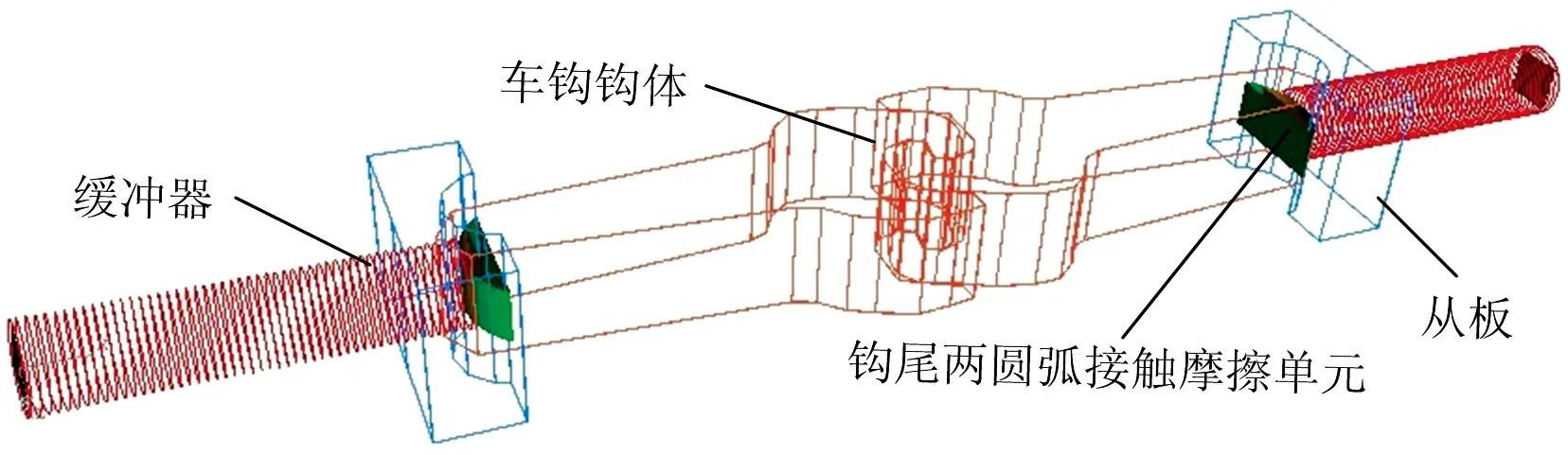
圖4 扁銷鉤緩裝置動力學模型

鉤尾“曲面—曲面”接觸摩擦單元通過兩圓弧上具有主從關系的移動點模擬接觸點位置的變化，并聯合使用接觸力元和摩擦力元建立具有接觸摩擦特性的模型，能夠準確模擬鉤尾圓弧面和前從板圓弧面的接觸摩擦作用。根據接觸原理和庫侖摩擦模型，接觸點處的接觸力Fgc和摩擦力Ff分別為

Fgc=Kcxc+Ccvc

(13)

(14)

式中：Kc和Cc分別為兩接觸面間的接觸剛度和阻尼；xc和vc分別為接觸點上兩物體的相互浸入位移和速度；vr為接觸點相對速度；vf為靜摩擦臨界速度；μ為摩擦系數。

緩沖器模型是具有遲滯特性的非線性模型，其加載與卸載特性曲線定義為2個以其行程為變量的函數fu(x)和fl(x)。定義切換速率ev來避免緩沖器阻抗力在加載和卸載切換時的不連續跳躍。緩沖器的數學模型為

FC=

(15)

其中：FC為當前緩沖器作用力； sign(x, Δv)為符號函數；Δv為緩沖器相對速度。

扁銷止擋的數學模型為

M1(αc)=

(16)

其中：M1(αc)為鉤尾扁銷止擋提供的回復力矩；αc為當前車鉤轉角；αfree為車鉤最大自由轉角；l為2個連掛車鉤鉤尾銷中心的距離。

2.3 雙機重聯牽引重載列車動力學模型

基于單節機車和鉤緩裝置的子結構模型，采用子結構方法建立如圖5所示的雙機重聯牽引重載列車動力學模型，編組方式為“HX型機車+HX型機車+貨車”，其中每臺HX型機車都由2個單節機車組成，每個單節機車間通過鉤緩裝置連接，貨車簡化為僅具有縱向自由度的單質點模型。采用輪軸處施加電機扭矩的方式模擬機車電制動力，具體方式是在每條輪對中心點施加1個與前進方向相反的扭矩，同時在構架相應位置上施加反向扭矩模擬實際軸重轉移情況。

2.4 簡化道岔模型

我國重載鐵路道岔由基本軌、轉轍區、連接部分、轍岔區等幾個部分組成，重載列車側向通過道岔時，轉轍區和轍岔區鋼軌型面變化、固定轍叉有害空間等都會引起頻率較高的輪軌沖擊作用。這些高頻輪軌作用力對道岔區段鋼軌疲勞損傷問題具有很大影響，在進行道岔區段輪軌動力學分析和道岔結構疲勞分析時需要重點關注。而本文主要關注重載列車側向過岔時的機車運行安全性和車鉤動態特性，進行濾波或平滑處理后的輪軌力響應只保留較低頻率部分，加之我國12號重載鐵路道岔側向通過速度較低，因此可以不考慮道岔轉轍區和轍岔區鋼軌型面變化帶來的沖擊效應，將其簡化為具有相同線路線形的S形曲線。該簡化方法的可行性將在下一節通過數據對比分析進行驗證。

圖5 雙機重聯牽引重載列車動力學模型

2.5 動力學模型驗證

除了簡化的S形曲線道岔模型外，本文還建立了考慮轉轍區和轍岔區鋼軌型面變化的12號道岔結構模型，然后分別采用該實際道岔模型和簡化道岔模型進行某雙機重聯牽引萬噸重載列車側向通過12號道岔試驗的數值模擬計算，通過計算結果與試驗數據對比分析來驗證本文模型的正確性。重載列車動力學模型和簡化道岔模型的部分參數見表2，車鉤鉤尾摩擦系數取0.20。計算中軌道不平順采用由鐵科院綜合檢測車在既有線路實測得到的軌道幾何不平順，緩沖器阻抗特性曲線由重載線路試驗實測數據通過擬合插值處理得到。計算所得輪軌力和運行安全性指標均采用“2 m”平滑方式進行處理。

表2 仿真計算部分結構參數

該機車滿級電制時單軸電制動力約為64 kN，根據車輪半徑換算成扭矩為40 kN·m，電制動力輸入曲線假設為每軸電機扭矩在0～5 s時間內從0線性增大至40 kN·m，在5～30 s時間內始終保持為40 kN·m。不同電制級位的電制動力輸入曲線通過該滿級電制輸入曲線乘以對應級位百分比的方式得到。

需要說明的是，由于第4組車鉤后鉤與貨列相連，其鉤尾的平面接觸在一定程度上限制了它的水平偏轉，因此最大車鉤轉角出現在第3組車鉤處，故以下選取第3組車鉤轉角和第3節機車第2位轉向架第1軸的運行安全性指標進行分析，后文不再贅述。

30%電制工況下計算和試驗所得重載機車側向過岔時車鉤轉角、脫軌系數的波形分別如圖6和圖7所示。從圖6和圖7可以看出：2個道岔模型的計算結果與試驗數據相比都具有一致的變化趨勢，車鉤轉角都在進、出道岔導曲線位置出現峰值，都在通過道岔后仍保持在2°左右，且其最大值也未見明顯差異；2種道岔模型計算所得車鉤轉角和脫軌系數較為接近，表明鋼軌型面變化對機車動力學和車鉤動態特性的影響并不十分明顯；通過以上對比分析，驗證了本文重載列車動力學模型的正確性，表明該模型能夠較好地模擬此類重載機車側向通過道岔的動力學問題。

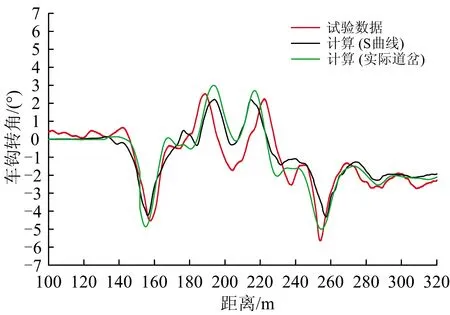
圖6 第3組車鉤后鉤轉角計算和試驗波形圖

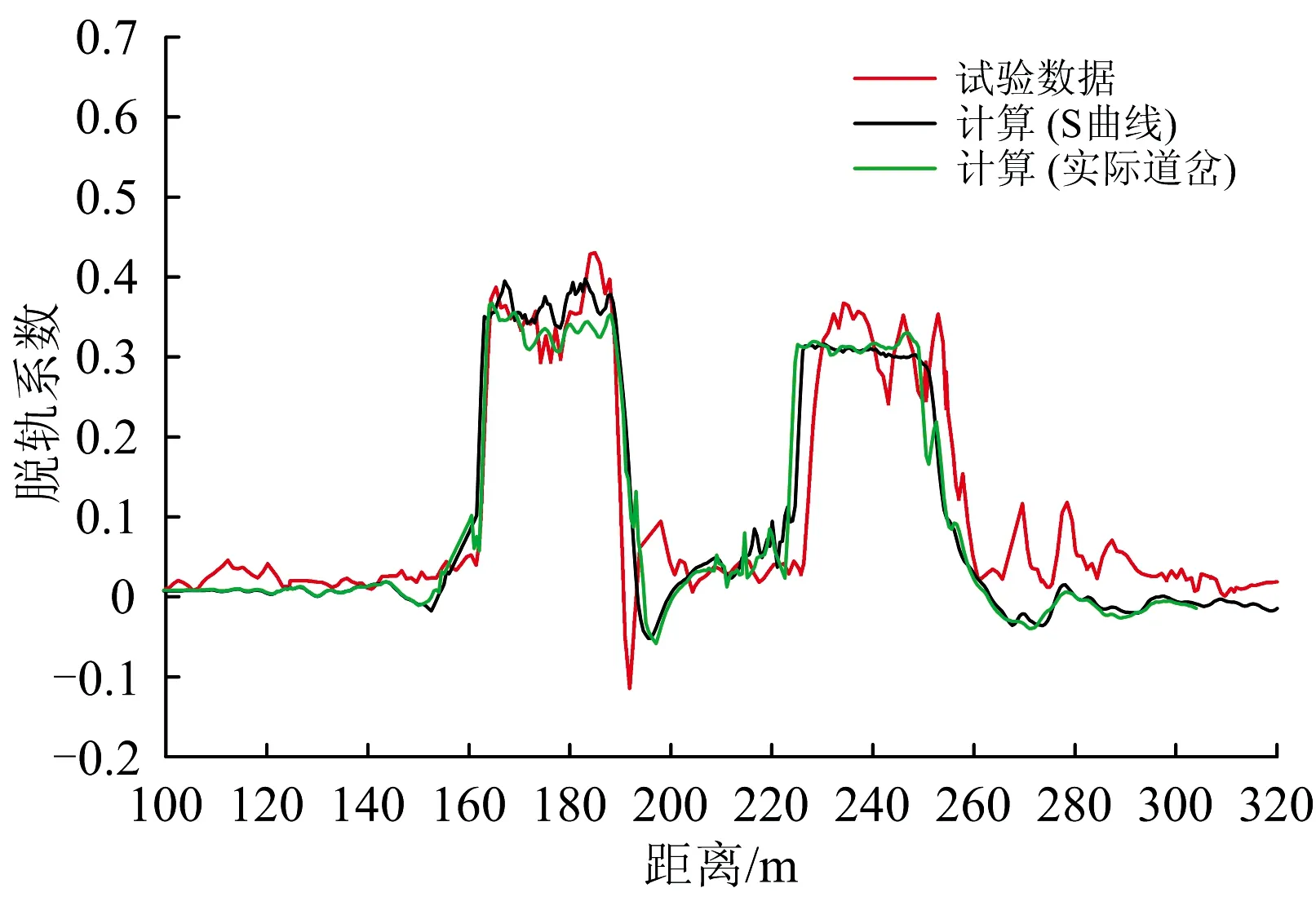
圖7 脫軌系數計算和試驗波形圖

3 數值計算分析

采用重載列車側向過岔動力學模型，分別計算不同機車電制級位和鉤尾摩擦系數下的動力學響應，分析這2個因素對重載機車運行安全性和車鉤轉角的影響規律。

3.1 機車電制級位的影響

假設電制級位在10%～100%范圍內每隔10%取值，分別計算不同電制級位下重載列車側向通過12號道岔的動力學響應。不同電制級位下前鉤轉角、脫軌系數、輪軸橫向力的波形分別如圖8—圖10所示。前鉤和后鉤轉角、脫軌系數、輪軸和輪軌橫向力隨電制級位的變化曲線分別如圖11—圖13所示。從圖中可以看出：①機車側向過岔時車鉤轉角最大值隨著電制動力的增大而逐漸增大；②電制級位大于50%時，重載機車側向過岔時的動態車鉤轉角明顯大于第1節的準靜態值，電制級位從50%增大至100%時前鉤轉角由6.01°增大至9.64°；③脫軌系數和輪軸橫向力在道岔區段曲線上均保持較高水平，其最大值在10%～50%電制級位范圍內基本保持不變，而在電制級位大于50%后隨著車鉤轉角的顯著增大也呈明顯增大趨勢；并且當100%電制級位時輪軸橫向力達到106 kN，已超出依據標準TB/T 2360—1993[14]得到的97 kN限值。④從圖11可以看出連掛車鉤前鉤轉角的始終大于后鉤，這與第1節靜態計算分析結果相同。

綜合分析，機車側向過岔的電制動力對其運行安全性具有重要影響作用，隨著電制動力的增大，車鉤轉角逐漸增大，車鉤壓力的橫向分力隨之增大，進而導致脫軌系數、輪軸橫向力等機車安全性指標明顯增大。因此為了保證重載列車側向通過12號道岔的安全性，應嚴格控制機車電制力級位在80%以下。

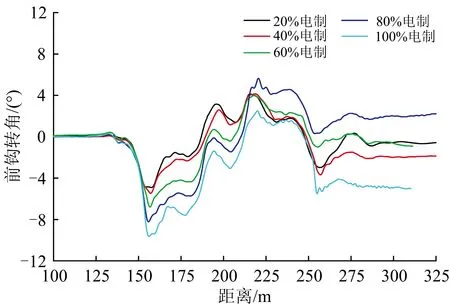
圖8 不同電制級位下重載機車側向過岔前鉤轉角波形

圖9 不同電制級位下重載機車側向過岔脫軌系數波形

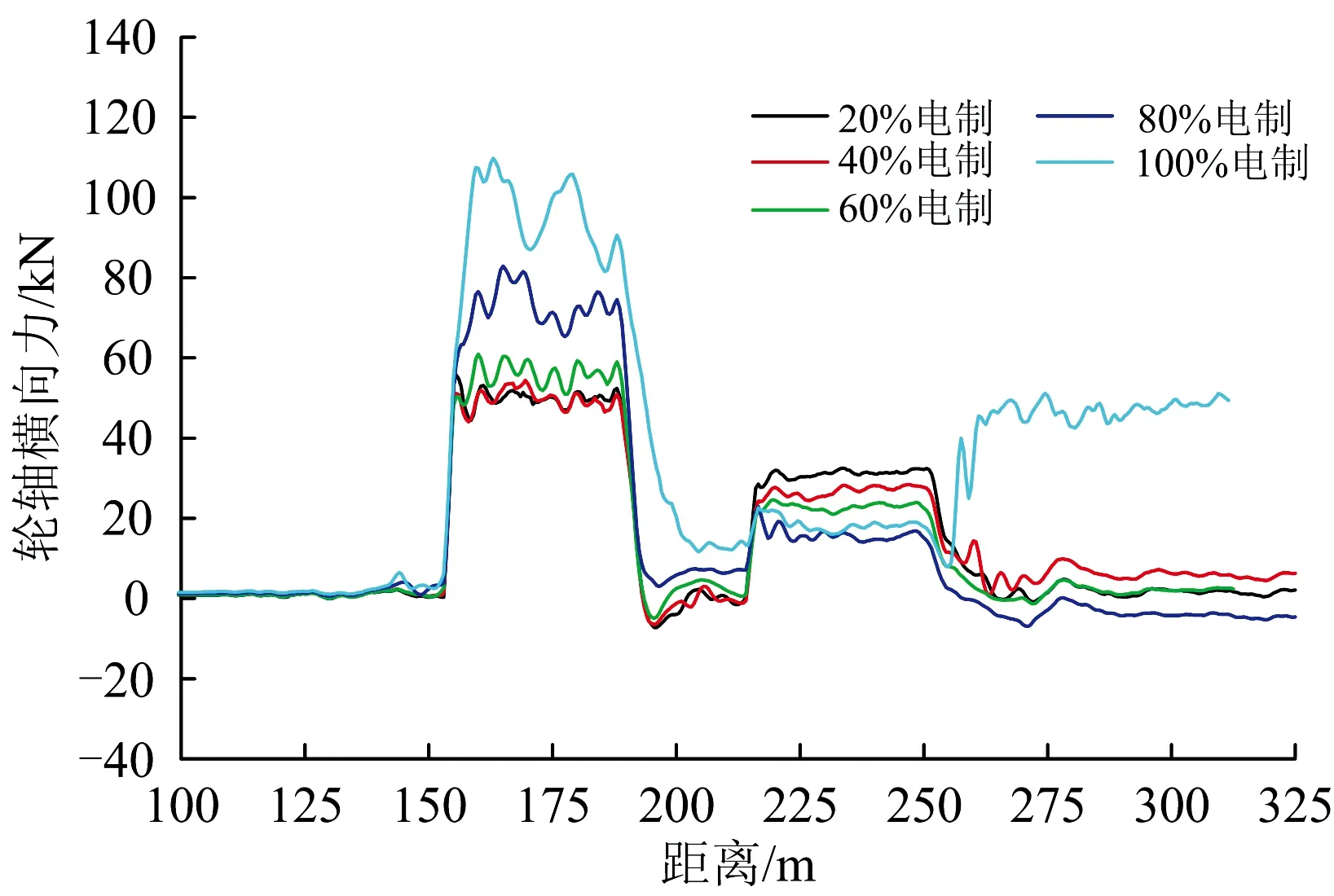
圖10 不同電制級位下重載機車側向過岔輪軸橫向力波形

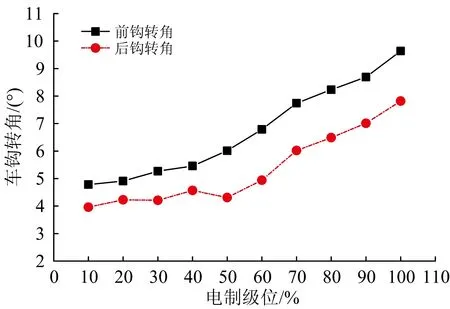
圖11 重載機車側向過岔前鉤和后鉤轉角隨電制級位變化曲線

圖12 重載機車側向過岔脫軌系數隨電制級位變化曲線

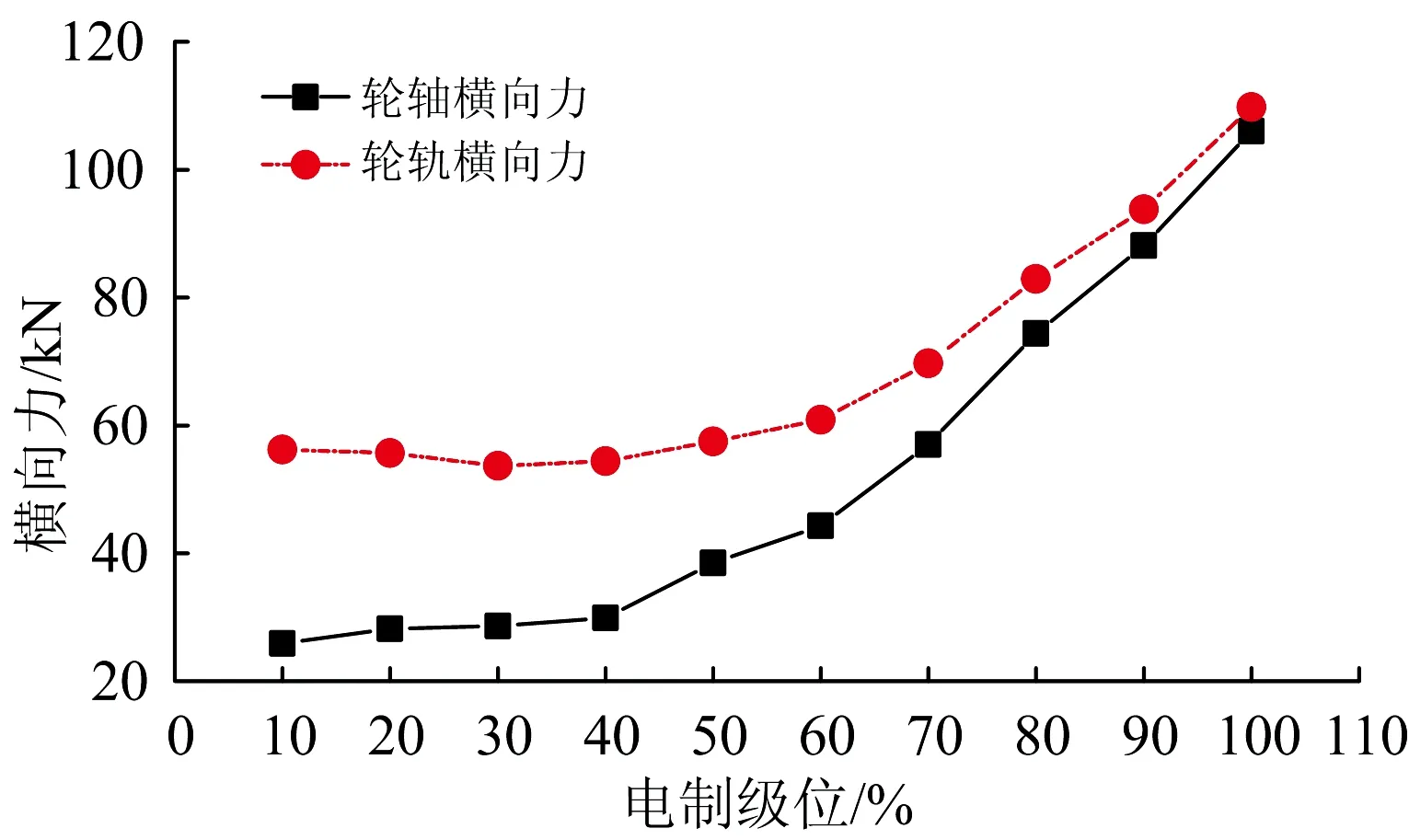
圖13 重載機車側向過岔輪軸橫向力和輪軌橫向力隨電制級位變化曲線

3.2 鉤尾摩擦系數的影響

機車電制級位設為80%，其他參數保持不變。假設鉤尾摩擦系數在0.05～0.40范圍內每隔0.05取值，分別計算不同鉤尾摩擦系數下重載機車電制側向通過12號道岔的動力學響應。前鉤和后鉤轉角、脫軌系數、輪軸和輪軌橫向力隨摩擦系數的變化曲線分別如圖14—圖16所示。從圖中可以看出：隨著鉤尾摩擦系數的增大，機車側向過岔時車鉤轉角最大值逐漸減小，車鉤穩鉤能力逐漸增強；當摩擦系數μ≤0.10時，由于鉤尾摩擦約束較小，車鉤在進出道岔位置均會發生大幅偏轉，前鉤轉角最大值達到9°，并且通過道岔后依然保持較大偏轉角；當摩擦系數逐漸增大時，鉤尾摩擦約束增強，摩擦系數μ≥0.30時前鉤轉角最大值均在4°以內，且降幅減小；與此同時，脫軌系數和輪軸橫向力表現出與車鉤轉角一致的變化規律，均隨著摩擦系數的增大而逐漸較小，并且在摩擦系數μ≥0.30時減小幅度變得不明顯。

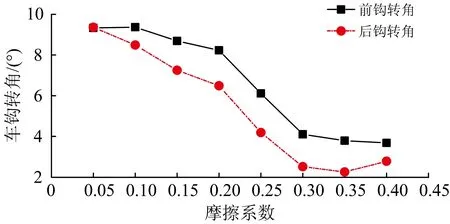
圖14 重載機車側向過岔前鉤和后鉤轉角隨鉤尾摩擦系數變化曲線

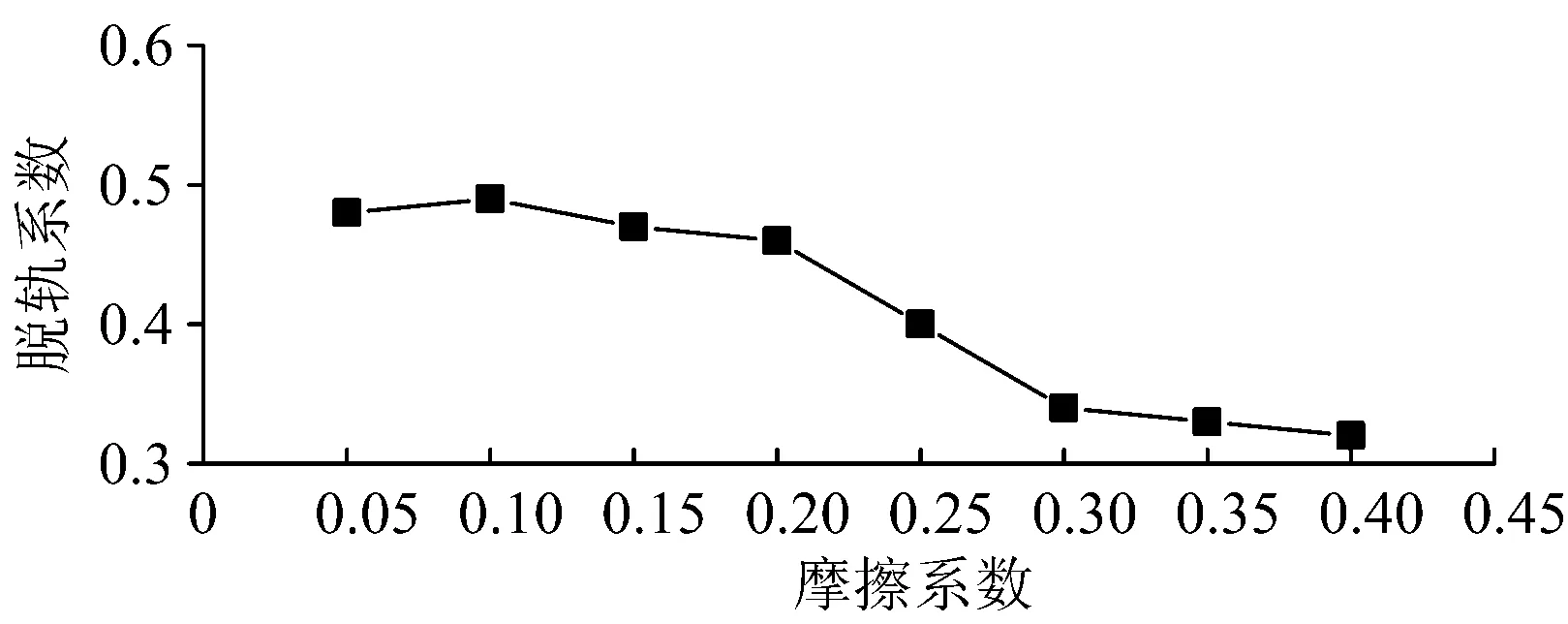
圖15 重載機車側向過岔脫軌系數隨鉤尾摩擦系數變化曲線

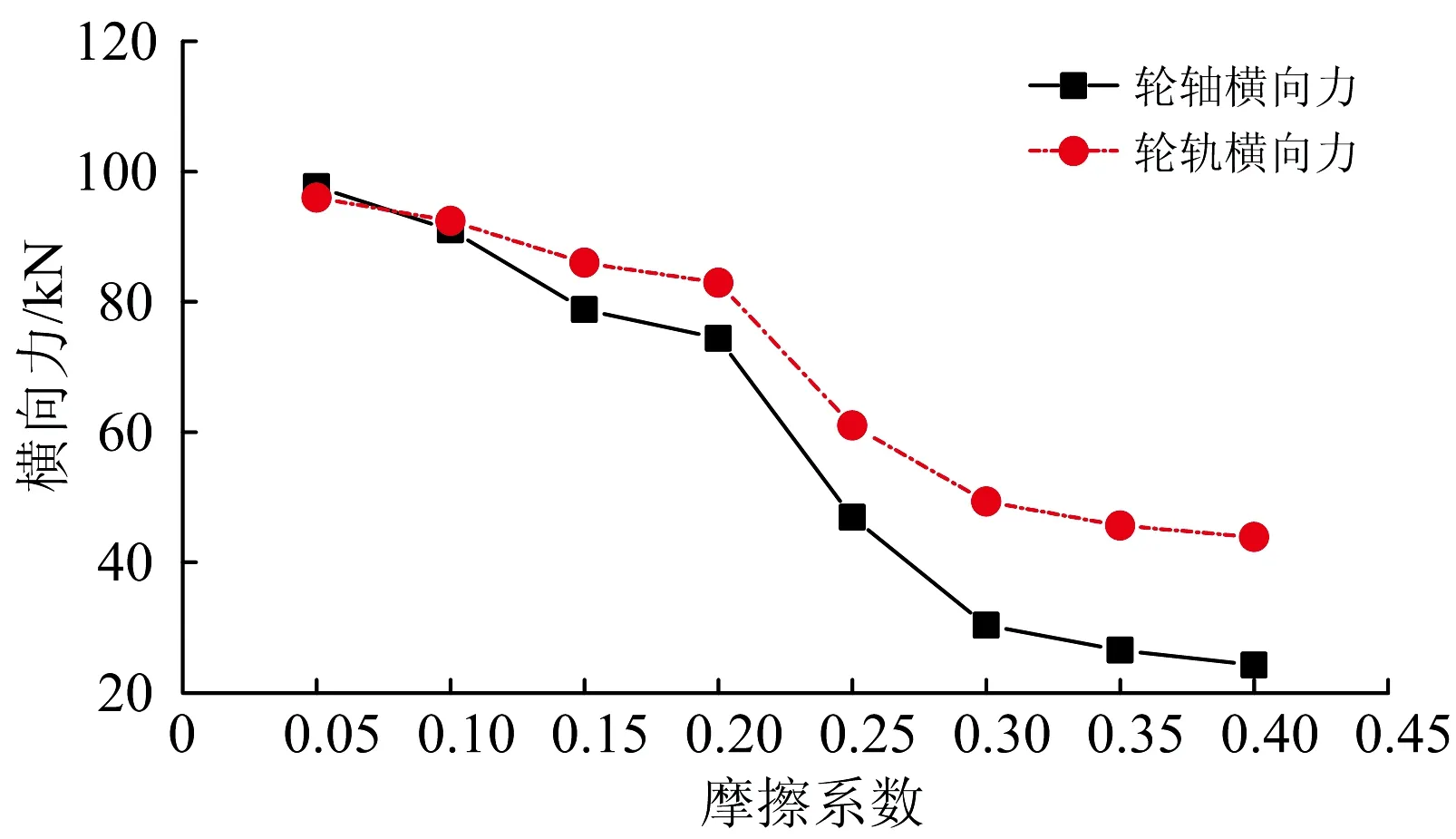
圖16 重載機車側向過岔輪軸和輪軌橫向力隨鉤尾摩擦系數變化曲線

總體而言，鉤尾摩擦系數對于電制側向過岔時機車及車鉤動態響應均具有較大影響，隨著摩擦系數的增大，車鉤穩鉤能力增強，車鉤轉角及安全性指標明顯減小。因此可以通過改進加工工藝或選用高摩擦系數的鉤尾結構材質提高其接觸摩擦系數，其合理控制范圍應為0.20～0.30。

4 結 論

(1)理論推導曲線線路上受壓連掛車鉤準靜態水平轉角的計算公式，分析發現車鉤轉角隨著曲線半徑的減小而逐漸增大，且前鉤轉角始終大于后鉤轉角。

(2)采用SIMPACK軟件和子結構方法建立重載列車電制側向過岔動力學模型，其中鉤緩裝置模型包括鉤尾“曲面—曲面”接觸摩擦單元、非線性遲滯特性緩沖器單元和扁銷止擋單元，道岔側向線路簡化為不考慮轉轍區和轍岔區鋼軌型面變化的S形曲線。該模型計算結果與試驗數據具有較好一致性，能夠準確模擬重載機車電制側向過岔時的動力學問題。

(3)機車電制動力對其側向過岔時運行安全性具有重要影響作用，隨著電制級位的提高車鉤轉角逐漸增大，導致機車安全性指標明顯增大，因此重載列車側向過岔時應將機車電制級位控制在80%以下。

(4)車鉤鉤尾摩擦系數對于重載機車電制側向過岔時系統動態響應也具有較大影響，隨著摩擦系數的增大，車鉤穩鉤能力增強，車鉤轉角及安全性指標明顯減小，其合理控制范圍應為0.20～0.30。