中等雷諾數(shù)方柱繞流的直接數(shù)值模擬及渦系分析

王建春，吳乘勝，王 星，徐金秀

（1.中國船舶科學(xué)研究中心 水動力學(xué)重點實驗室，江蘇 無錫214082；2.江南計算技術(shù)研究所，江蘇 無錫214081）

0 引 言

湍流的數(shù)值模擬主要有雷諾平均數(shù)值模擬、大渦模擬以及直接數(shù)值模擬（Direct Numerical Simulation，DNS）三種方法，每種方法都有其重要的作用和地位，不可能被其他手段所完全代替。工程上研究湍流普遍采用的數(shù)值模擬方法是雷諾平均數(shù)值方法。這種方法的計算相對比較簡單，但是獲得的信息比較少，很難模擬到湍流的全部擬序結(jié)構(gòu)；此外，它致命的缺陷是湍流模型不具有普適性。大渦模擬的主要思想是大尺度湍流渦系結(jié)構(gòu)采用直接數(shù)值模擬方法求解，而小尺度湍流渦系結(jié)構(gòu)則采用亞格子模型的方法來模擬；因而，其不足之處在于無法準(zhǔn)確模擬小尺度渦系結(jié)構(gòu)以及小尺度渦的耗散過程。

湍流數(shù)值方法中最準(zhǔn)確的是DNS[1-3]。它不需要任何湍流模型，直接數(shù)值求解三維瞬態(tài)流動控制方程，能夠捕捉到不同瞬時的湍流細(xì)致流場結(jié)構(gòu)，因而可以了解湍流的精細(xì)流場、流動現(xiàn)象和流動規(guī)律等。DNS計算所得結(jié)果既可以用來深入研究湍流的流動結(jié)構(gòu)，還可以用來檢驗和發(fā)展各種雷諾平均數(shù)值方法的湍流模型，檢驗大渦模擬的各種亞網(wǎng)格尺度模型以及檢驗湍流實驗的測量精確度等。

制約DNS工程應(yīng)用的關(guān)鍵瓶頸，在于其為了能夠模擬所有尺度的湍流脈動以及各種尺度的擬序結(jié)構(gòu)，求解算法需要具有非常高的時空分辨率，即數(shù)值模擬中需要足夠多的時間步和足夠精細(xì)的網(wǎng)格。通常對于充分發(fā)展的湍流，需要105以上的時間積分步，而網(wǎng)格的數(shù)量則隨雷諾數(shù)呈指數(shù)增長。也就是說DNS所需的內(nèi)存和計算量非常大，具有一定工程意義的中等以上雷諾數(shù)流動問題，需要使用超級計算機(jī)才能實現(xiàn)湍流的DNS模擬。

方柱繞流具有物體幾何外形簡單而流場結(jié)構(gòu)非常復(fù)雜的特性，是鈍體繞流研究的一種典型情況。將DNS用于柱體繞流的研究中，能夠獲得更加精細(xì)和準(zhǔn)確的流場結(jié)構(gòu)，無論是在理論研究上或是在工程應(yīng)用上都非常有意義。一方面，柱體繞流中的渦激振動現(xiàn)象、流固耦合現(xiàn)象、尾渦的相互干擾現(xiàn)象都特別明顯，復(fù)雜鈍體繞流現(xiàn)象的研究一般都是基于柱體繞流而展開的；另一方面，柱形材料結(jié)構(gòu)設(shè)計、船舶煙囪、房屋建筑和熱交換器等設(shè)計，流動誘發(fā)的振蕩[4]、聲學(xué)輻射[5]、海底管道水動力性能[6]研究等都會涉及到柱體繞流的研究；在海洋工程中還有一些像鉆井平臺的立管等結(jié)構(gòu)的繞流現(xiàn)象，也都可以采用柱體繞流的模型進(jìn)行研究。近年來，伴隨著計算機(jī)計算能力的提高，以及對一些新的現(xiàn)象比如展向漸變不穩(wěn)定模型的認(rèn)識的增加，都吸引了很多研究者的興趣，其中包含了大量的柱體繞流的DNS研究[7]。

在此背景下，本文通過自主設(shè)計和編制的DNS并行計算程序，開展了中等雷諾數(shù)二維方柱繞流的DNS模擬研究。文中首先開展了低雷諾數(shù)流動（Re=100）的DNS模擬，以及數(shù)值模擬的時空分辨率收斂性研究，通過與文獻(xiàn)結(jié)果的對比，對DNS程序進(jìn)行了初步驗證。隨后在“神威·太湖之光”超級計算機(jī)上，開展了中等雷諾數(shù)流動（Re=10 000）的DNS模擬，對流動中的渦系發(fā)展及演化過程進(jìn)行了分析，并通過與RANS和LES模擬結(jié)果的對比分析，展現(xiàn)了DNS在復(fù)雜精細(xì)流場模擬方面的優(yōu)勢。

1 控制方程及其離散

本文采用基于交錯網(wǎng)格的有限體積法求解不可壓縮N-S（Navier-Stokes）方程組，無量綱化積分形式控制方程組如下：

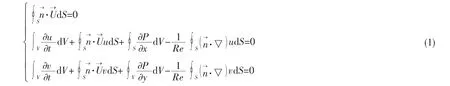
所謂的交錯網(wǎng)格，就是壓力、密度等物理量存儲在控制體P的中心，這個控制體稱為主控制體，如圖1（a）所示；將速度分量（u,v）分別存儲在主控制體的左右邊線和上下邊線位置處，再分別以此為中心，劃分速度分量u和v的控制體，如圖1（b）和圖1（c）所示。

圖1 交錯網(wǎng)格示意圖Fig.1 Description of staggered grid

離散后的方程組為：

式中各下標(biāo)的意義為：e，n，w，s代表控制體的四條邊，E，N，W，S代表控制體的中心位置，nb代表周圍臨近的節(jié)點。

數(shù)值求解中，壓力-速度耦合采用SIMPLE（Semi-Implicit Method for Pressure-Linked Equations）算法[8]處理；離散得到的代數(shù)方程組采用Gauss-Seidel迭代求解；時間步進(jìn)采用Euler隱式格式，對流項采用QUICK（Quadratic Upwind Interpolation of Convective Kinematics）格式，耗散項采用中心差分格式。具體離散求解過程可參考相關(guān)文獻(xiàn)[9]。

數(shù)值求解過程中，控制方程組的收斂判據(jù)為：所有控制體中連續(xù)性方程余量的最大值小于規(guī)定值；動量方程的速度余量減少一個數(shù)量級或者迭代次數(shù)達(dá)到5次[10]；壓力修正方程規(guī)定終止迭代時的范數(shù)與初始范數(shù)之比小于允許值。

2 并行算法

前面提到，DNS模擬所需的內(nèi)存和計算量非常大，具有一定工程意義的中等以上雷諾數(shù)流動問題，需要使用超級計算機(jī)通過并行計算才能實現(xiàn)湍流的DNS模擬。

并行計算方法[11]可以分為三類：基于消息傳遞的方法、基于共享存儲的方式和數(shù)據(jù)并行。基于消息傳遞的方法主要采用調(diào)用MPI函數(shù)庫的方法，屬于進(jìn)程級大粒度并行；基于共享存儲的方式主要采用Openacc編譯制導(dǎo)指令的方法，屬于線程級細(xì)粒度的并行。其中，MPI全稱消息傳遞界面（Message Passing Interface）是目前使用較為廣泛的并行計算處理方法。

在“神威·太湖之光”處理器架構(gòu)上，采用相對比較多的是消息傳遞結(jié)合共享存儲的方式。其中，MPI主要利用其主核來進(jìn)行消息傳遞并行計算；而Openacc則利用其單個主核下的眾核并行計算；二者的結(jié)合可以實現(xiàn)所謂的“二級并行”：進(jìn)程間的并行+進(jìn)程內(nèi)部線程的眾核并行。

本文的數(shù)值計算工作在“神威·太湖之光”超級計算機(jī)上開展，采用MPI[12]實現(xiàn)并行計算。之所以未采用MPI+Openacc二級并行，主要是因為本文采用的SIMPLE算法是一種半隱式的求解方法，壓力修正方程往往需要采用隱式迭代算法如高斯賽德爾算法進(jìn)行求解。此類隱式迭代算法的好處是收斂快，但這種算法本身實質(zhì)上是串行的，存在數(shù)據(jù)相關(guān)性，暫時無法實現(xiàn)Openacc眾核并行，雖可采用紅黑著色法代替之，但一定程度上使得迭代方法半顯式化了，導(dǎo)致計算收斂變慢，效果并不好。

MPI并行方法又可以分為數(shù)值算法并行和區(qū)域分解并行，目前使用較多的是后者，其基本的工作原理如圖2所示：圖中將一個大任務(wù)分解為多個子任務(wù)，每個子任務(wù)分配給一個進(jìn)程；進(jìn)程間的信息傳遞主要是將邊界處的值進(jìn)行交換或者插值處理，如圖中進(jìn)程5就需要同時與周邊四個進(jìn)程進(jìn)行邊界信息傳遞。圖中：MX是水平方向上的最大網(wǎng)格數(shù)，0、-1、MX+1和MX+2代表了用于交換信息的虛擬邊界。

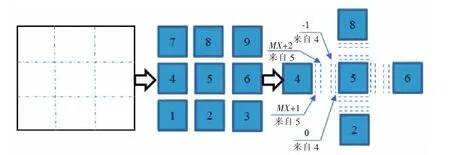
圖2 MPI區(qū)域分解并行過程示意圖Fig.2 Description of MPI domain decomposition for parallel computation

3 低雷諾數(shù)方柱繞流DNS模擬與分析

3.1 方柱繞流的物理幾何模型

圖3給出了二維方柱繞流的幾何模型，其中采用四個參數(shù)x1=11.1d，x2，y1，y2來確定方柱的具體位置；L=36d為計算域長度，H=100/7d為計算域?qū)挾龋琩為方柱長度。AB為進(jìn)口、CD為出口、BC為上邊界、AD為下邊界。

邊界條件定義如下：

入口處（AB）的邊界條件為均一來流，給定速度分量的大小：U=1，V=0。

出口邊界距離柱體足夠遠(yuǎn)，此時出口處的流動狀態(tài)達(dá)到充分發(fā)展?fàn)顟B(tài)，在流動方向上各參數(shù)梯度變化為0，即出口處應(yīng)為平滑流動。這里定義速度沿CD邊界法向變化為0，即?U/?n=0，?V/?n=0，n為界面法向。

對于物面邊界采用的是固壁邊界條件，固壁的速度邊界條件一般為無滑移邊界條件，即U=0，V=0。

上下邊界條件為軸對稱面邊界條件：流動的法向速度為零，而切向速度不應(yīng)該存在速度梯度，也就是V=0，?U/?y=0。

圖3 二維方柱繞流的物理幾何模型Fig.3 Physical geometry model of flow past a two-dimensional square cylinder

所有的壓力邊界條件都采用Neuman邊界條件。

3.2 低雷諾數(shù)方柱繞流DNS模擬及時空分辨率收斂性分析

為驗證計算程序，首先開展了低雷諾數(shù)（Re=100）方柱繞流DNS模擬研究，分別開展了計算的時間和空間分辨率收斂性研究。

（1）時間分辨率收斂性研究

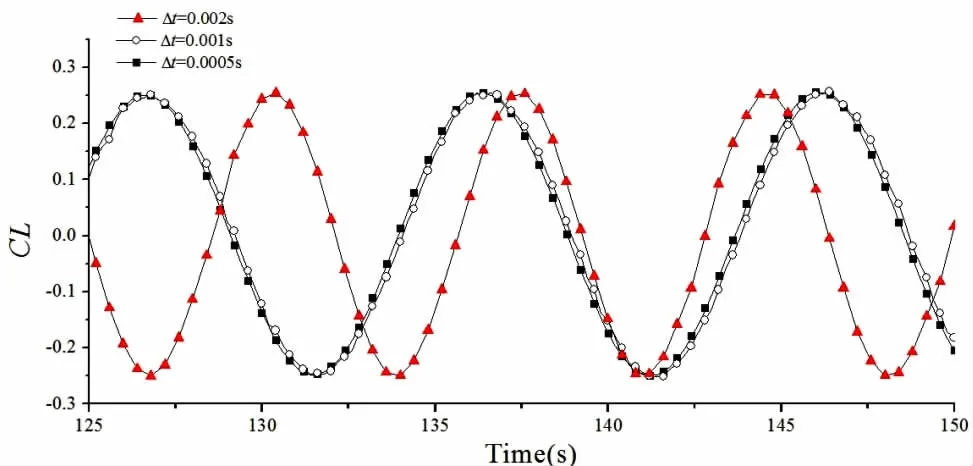
圖4 不同時間步長方柱升力系數(shù)時歷曲線（Re=100）Fig.4 Time history of lift coefficient for different time step(Re=100)

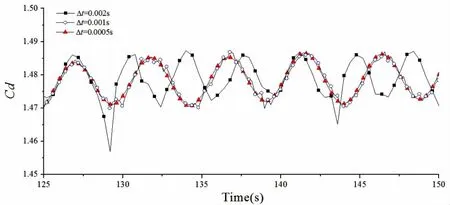
圖5 不同時間步長方柱阻力系數(shù)時歷曲線（Re=100）Fig.5 Time history of drag coefficient for different time step(Re=100)

圖4給出了網(wǎng)格數(shù)為672*300（空間分辨率為0.05，滿足Re=100時的DNS模擬要求）、時間步長分別為0.002 s、0.001 s和0.000 5 s時的方柱升力系數(shù)時歷曲線；圖5則給出了該網(wǎng)格下不同時間步長的方柱阻力系數(shù)時歷曲線。

從圖中可以看出，對于Re=100的方柱繞流，在該網(wǎng)格下，當(dāng)時間分辨率達(dá)到0.001 s時，計算結(jié)果已經(jīng)收斂了。

（2）空間分辨率收斂性研究

分別采用空間分辨率0.071、0.05和0.04的三套網(wǎng)格（對應(yīng)的網(wǎng)格數(shù)分別為450*200、672*300和810*355）進(jìn)行網(wǎng)格收斂性研究，時間步長根據(jù)前面的研究取為0.001 s。

圖6和圖7分別給出了不同空間分辨率時方柱升力系數(shù)和阻力系數(shù)時歷曲線。從圖中可以看出，當(dāng)空間分辨率達(dá)到0.05時，計算結(jié)果是收斂的。

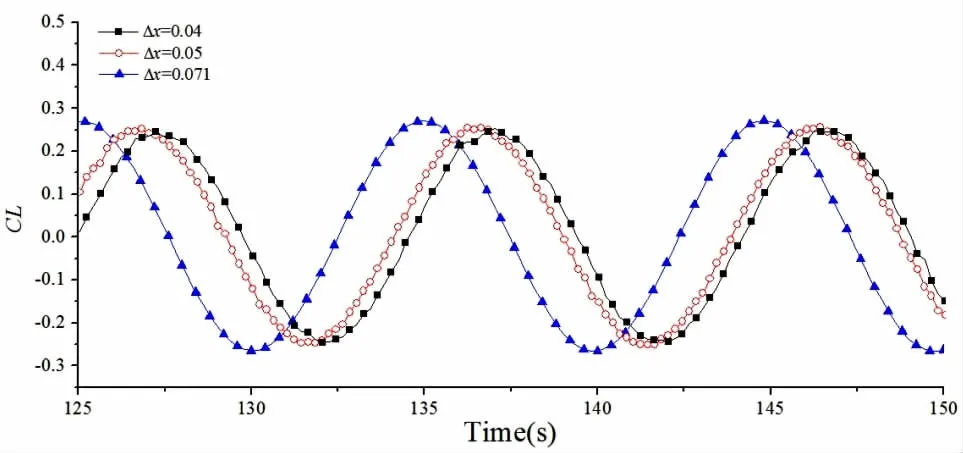
圖6 不同空間分辨率方柱升力系數(shù)時歷曲線（Re=100）Fig.6 Time history of lift coefficient for different spatial resolution(Re=100)

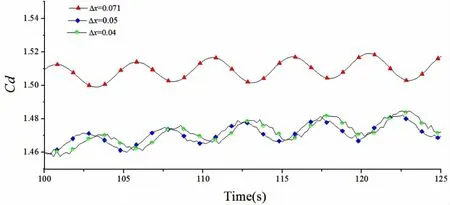
圖7 不同空間分辨率方柱阻力系數(shù)時歷曲線（Re=100）Fig.7 Time history of drag coefficient for different spatial resolution(Re=100)

表1給出了程序計算收斂后獲得的計算結(jié)果與相關(guān)文獻(xiàn)的對比。由表1和圖7可見，在Re=100時，計算所得方柱平均阻力系數(shù)為1.48，與Sohankar和Davision等人[13-15]計算得到的結(jié)果基本一致；而St數(shù)卻存在一定的偏差，主要原因可能是由于時間離散采用一階全隱格式，離散精度不夠高。

表1 計算結(jié)果與文獻(xiàn)的比較（Re=100）Tab.1 Comparison between computed results and the reference(Re=100)

圖8給出了一個周期內(nèi)尾流場中的卡門渦街變化過程。從t=180 s到t=189 s，方柱尾流中的漩渦完成一個周期下的運動，尾渦的變化過程如下：右下角產(chǎn)生新的小渦→右下角的小渦增大的過程中，右上角的大渦脫離壁面并向后方遷移→右下角小渦變成大渦→右下角大渦開始脫離壁面并向下游遷移，右上角產(chǎn)生新的小渦→右上角小渦增大變成大渦、大渦開始脫離壁面并向下游遷移→右下角產(chǎn)生新的小渦。

通過以上低雷諾數(shù)方柱繞流DNS模擬及時空分辨率收斂性分析可知，計算程序的設(shè)計編制是正確的；在滿足DNS要求的時空分辨率情況下，計算結(jié)果是準(zhǔn)確可靠的。

4 中等雷諾數(shù)方柱繞流DNS模擬與渦系分析

對Re=10 000的二維方柱繞流進(jìn)行了DNS模擬，計算域根據(jù)文獻(xiàn)[17]確定：x1/d=5，L/d=21，H/d=11.4；數(shù)值模擬中，時間步長取為0.000 5 s，空間分辨率為1.0/70（網(wǎng)格總數(shù)103萬），滿足DNS模擬對時空分辨率的要求。

4.1 升力及平均流場計算結(jié)果

圖9給出了方柱升力系數(shù)的時歷曲線（部分）。從圖中可以看出，升力系數(shù)隨時間的變化不再具有明顯的周期性。將升力系數(shù)進(jìn)行頻譜分析可以得出無量綱參數(shù)St數(shù)；從圖9右側(cè)的頻譜圖可以看出，數(shù)值模擬得到的St值為0.128，與實驗[15]結(jié)果St=0.130基本一致。

圖9 方柱升力系數(shù)時歷曲線圖及其頻譜圖（Re=10 000）Fig.9 Time history of lift coefficient and corresponding frequency spectrum

圖10左側(cè)給出了經(jīng)過77 s統(tǒng)計平均后得到的上表面水平速度平均值的分布云圖，右側(cè)給出了三個位置上的平均水平速度沿垂向的分布（上）及與文獻(xiàn)[17]計算結(jié)果（下）的對比。

由圖中可以看出：①本文計算得到的方柱上表面的平均水平速度分布與文獻(xiàn)[17]的計算結(jié)果基本一致；②分離泡的外緣的平均速度剖面類似自由剪切層；③一個大的回流區(qū)幾乎覆蓋了方柱整個上表面；④x=-0.4～0.3之間（方柱前角點后方），有一個明顯二次回流區(qū)域。上述流場特征，都和文獻(xiàn)[17]中的計算結(jié)果完全一致。

4.2 渦系結(jié)構(gòu)分析

圖11給出了t=105 s時刻，本文計算得到的流場渦系結(jié)構(gòu)（下）與文獻(xiàn)[17]計算結(jié)果（上）的對比。從圖中可以看出，對于方柱尾流場特征及渦系結(jié)構(gòu)，本文計算結(jié)果與文獻(xiàn)[17]中的基本一致：在緊鄰柱體后方的流場中，形成很多的小尺度渦和渦絲，這些小尺度渦和渦絲相互融合形成大渦并與其他大渦相互作用使其破裂成小尺度渦和渦絲；在遠(yuǎn)離方柱的地方，這些小尺度渦和渦絲通過融合的方式形成相對比較穩(wěn)定的流場結(jié)構(gòu)，比如圖中所示的單極子型渦和偶極子型渦。

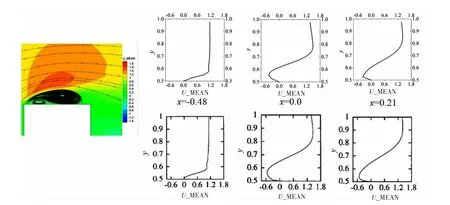
圖10 方柱上表面平均水平速度云圖及速度分布曲線圖Fig.10 Mean u-velocity contour and profiles for three locations along upper side of cylinder

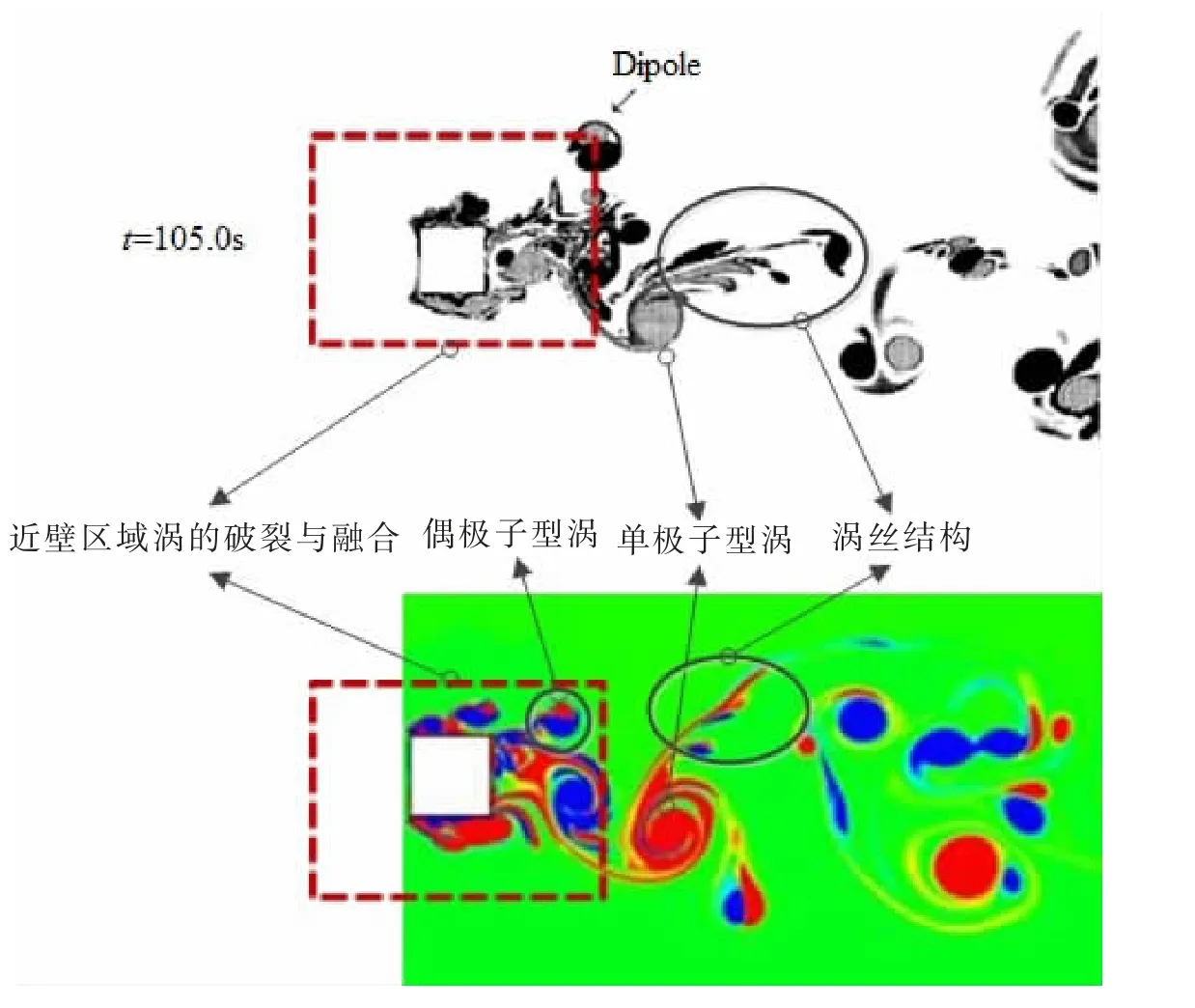
圖11 流場渦系結(jié)構(gòu)計算結(jié)果與文獻(xiàn)[17]的對比（t=105 s）Fig.11 Comparison of vortex structures for the computed results and the Ref.[17](t=105 s)

圖12給出了更為細(xì)致的流場渦系結(jié)構(gòu)圖（t=105s）。從圖中可以看出，DNS模擬很好地捕捉到了鈍體繞流的典型流場結(jié)構(gòu)和特征，如：分離泡，偽三角區(qū)，單極子型渦、雙極子型渦的形成和遷移過程，以及小尺度渦的耗散過程等。

分離泡[16]是一種在航空航天以及其他工程領(lǐng)域中都廣泛存在的轉(zhuǎn)捩現(xiàn)象：在中低雷諾數(shù)下，流動常處于層流狀態(tài)；當(dāng)流體流過柱體前緣后，由于其抗拒逆壓梯度的能力較弱，容易產(chǎn)生分離；層流分離后，剪切層離開壁面，由于速度剖面不穩(wěn)定，很快導(dǎo)致轉(zhuǎn)捩；轉(zhuǎn)捩后的湍流裹入能量使邊界層再附著，從而形成分離泡。

偽三角區(qū)是指方柱前緣分離泡和由主渦誘導(dǎo)產(chǎn)生的二次渦構(gòu)成的形狀類似三角形的區(qū)域。偽三角區(qū)域是鈍體繞流動力學(xué)的基礎(chǔ)流動結(jié)構(gòu)，屬于一類相對較穩(wěn)定的流場結(jié)構(gòu)。所謂穩(wěn)定是指：在偽三角區(qū)域內(nèi)，大部分區(qū)域都是吸附在固體壁面上的，盡管它會振蕩和變形，但是二次渦形狀無論在時間還是空間上都是定常的，分離泡則有規(guī)律地在最大和最小距角之間輕微地變化。

圖13給出了t=105-108 s時段方柱繞流渦量場的變化過程。從圖中可以清楚地看出各種渦的形成、脫落、發(fā)展、遷移和耗散等過程：

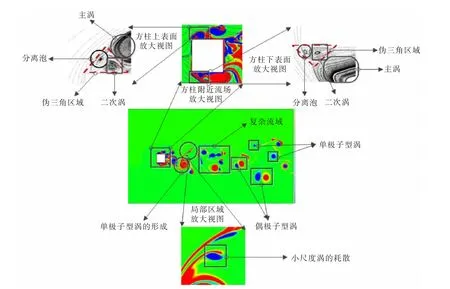
圖12 流場細(xì)觀渦系結(jié)構(gòu)（t=105 s）Fig.12 Meticulous vortex structure in the flow field(t=105 s)

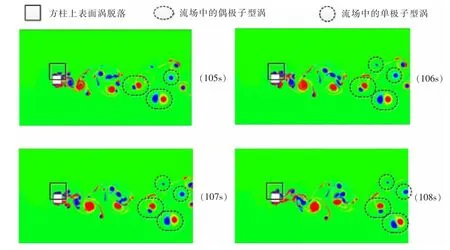
圖13 方柱繞流渦量場變化過程（Re=10 000）Fig.13 Description of the vortex contour changing with time simulated by DNS(Re=10 000)

在Re=10 000情況下，渦開始從側(cè)邊發(fā)生脫落，但并不是從分離點發(fā)生脫落的，而是從緊鄰偽三角區(qū)域后方的主渦的頂部發(fā)生脫落的。

在柱體后面的流場中，會形成很多的小尺度渦和渦絲。這些小尺度渦和渦絲會在遠(yuǎn)離方柱的地方，通過融合的方式形成相對比較穩(wěn)定的流場結(jié)構(gòu)，如單極子型渦和偶極子型渦。隨著流體的遷移運動，單極子型渦和偶極子型渦在遷移過程中基本形態(tài)不會發(fā)生變化，偶極子渦中的兩個大小相等的對稱反向渦相對位置保持不變。這說明在流場中，單極子和偶極子型渦是比較穩(wěn)定的流動結(jié)構(gòu)；相對而言，流場中的其它類型的渦則較不穩(wěn)定，往往會因為相互間的作用發(fā)生變形甚至破裂，比如在流場內(nèi)的各種渦量大小不對等的渦結(jié)構(gòu)。

Re=10 000的方柱繞流尾流中，渦的相互作用非常劇烈，特別是大渦與小渦之間的相互作用，在這種作用下往往會觸發(fā)大渦的破裂以及再形成。大渦的破裂是因為在其遷移過程中，由于遷移速度較快與后方遷移速度較小的渦發(fā)生了碰撞，破壞了大渦的穩(wěn)定性；原先的大渦發(fā)生了破裂，破裂后形成了一個較小的渦核以及很多的渦絲；小的渦核繼續(xù)向著下游遷移并由于渦核的吸引作用，不斷地發(fā)展變大，最后會形成新的單極子型渦；渦絲則有一部分會耗散在流場中，另一部分會被渦核吸附形成新的大渦。

在方柱下表面也明顯發(fā)生了渦的破裂現(xiàn)象，破裂后的渦一部分向下游遷移，另一部分則吸附到柱體表面上。這種渦的破裂是因為方柱下表面層流發(fā)生轉(zhuǎn)捩所致。

圖11-13也展現(xiàn)了小尺度渦的耗散過程。該耗散過程主要是由于人工粘性和數(shù)值耗散引起的，其機(jī)制與能量的耗散相似，因而一定程度上能夠反映出小尺度渦的能量耗散過程：從105 s時刻開始，順時針旋轉(zhuǎn)渦和逆時針旋轉(zhuǎn)渦的渦量幅值是相等的；在106 s、107 s瞬時，逆時針旋轉(zhuǎn)渦的渦量幅值保持不變，而順時針旋轉(zhuǎn)渦的渦量幅值則逐漸變小；最后渦量幅值逐漸趨于0，流場中已經(jīng)不能清晰地看到該渦結(jié)構(gòu)。這個過程就是小尺度渦的能量耗散過程。

4.3 DNS、RANS及LES模擬結(jié)果對比

由于DNS模擬計算量巨大，因而本文也嘗試采用計算量相對較小的RANS和LES方法，開展方柱繞流（Re=10 000）的數(shù)值模擬，研究這兩種方法能否準(zhǔn)確模擬此類復(fù)雜精細(xì)流場。

圖14給出了采用RANS方法模擬得到的Re=10 000方柱繞流的渦量場及其變化過程（t=105-108 s），其中湍流采用SST k-ω模型處理。

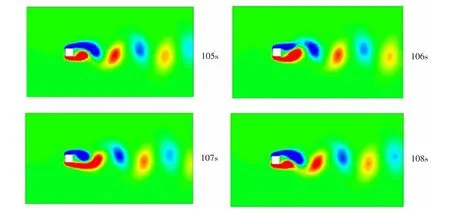
圖14 方柱繞流渦量場RANS模擬結(jié)果（Re=10 000）Fig.14 Description of the vortex contour changing with time simulated by RANS(Re=10 000)

從圖中可以看出，相比于DNS模擬，RANS模擬有以下幾點不足之處：

（1）只能捕捉到一些較大的渦結(jié)構(gòu)，無法獲得典型的鈍體繞流場基本結(jié)構(gòu)特征，例如偽三角區(qū)域和分離泡結(jié)構(gòu)等；

（2）在尾流場中沒有不同尺度的渦結(jié)構(gòu)，也就無法模擬小尺度渦是如何耗散的過程；

（3）渦的脫落只發(fā)生在尾流場中，而不是出現(xiàn)在方柱上表面的偽三角區(qū)域后方。

以上對于流場特征及渦系結(jié)構(gòu)的分析，說明RANS方法無法準(zhǔn)確模擬諸如方柱繞流之類的復(fù)雜精細(xì)流動。

圖15給出了采用LES方法模擬得到的Re=10 000方柱繞流的渦量場及其變化過程（t=105-108 s），其中亞格子模型采用Smagorinsky-Lilly模型。

從圖中可以觀察到LES模擬與DNS模擬結(jié)果有一些相一致的現(xiàn)象：如渦的脫落不是在方柱前緣的分離點而是在靠近偽三角區(qū)域后方的頂端附近；在t=106 s時刻，下表面的大渦也發(fā)生了破裂現(xiàn)象等。

但相比于DNS模擬，LES模擬得到的尾流場中的渦結(jié)構(gòu)不穩(wěn)定，很容易隨著流動發(fā)生各種拉伸和變形，沒有相對穩(wěn)定的單極子型渦和偶極子型渦結(jié)構(gòu)。這也就是在復(fù)雜精細(xì)流場模擬方面，DNS相比于LES的更具優(yōu)勢的表現(xiàn)之一。

圖15 方柱繞流渦量場LES模擬結(jié)果（Re=10 000）Fig.15 Description of the vortex contour changing with time simulated by LES(Re=10 000)

圖16給出了DNS、LES和RANS三種數(shù)值模擬方法計算獲得的方柱升力系數(shù)時歷曲線。從圖中可以看出：

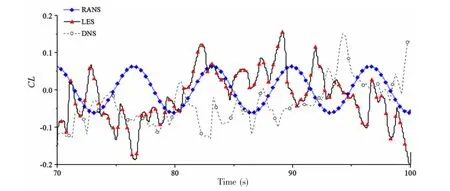
圖16 方柱升力系數(shù)時歷DNS、LES和RANS計算結(jié)果（Re=10 000）Fig.16 Time history of lift coefficient computed by DNS,LES and RANS(Re=10 000)

RANS數(shù)值模擬得到的方柱升力系數(shù)時歷曲線具有明顯的周期性，周期約為6.5 s（St=0.154）。然而文獻(xiàn)[15]指出，對于方柱繞流，當(dāng)Re＞1 000時流動就已經(jīng)不再是層流狀態(tài)了。因此Re=10 000時，柱體表面的渦脫落過程不再具有固定的周期，從而升力系數(shù)也不應(yīng)該是周期性變化的，這與RANS模擬的結(jié)果是矛盾的。由此可見，采用RANS方法模擬該雷諾數(shù)下的方柱繞流，其流場模擬結(jié)果是不準(zhǔn)確的。

對于LES和DNS模擬，計算得到的方柱升力系數(shù)時歷曲線都是不規(guī)則的，沒有表現(xiàn)出明顯的周期性，無法直接比較，因而通過對升力系數(shù)時歷曲線的頻譜分析，得到無量綱參數(shù)斯特勞哈爾數(shù)（St），從而便于比較。

圖17給出了LES和RANS數(shù)值模擬得到的方柱升力系數(shù)時歷曲線的頻譜分析。表2給出了頻譜分析得到的St，表中同時給出了實驗結(jié)果。從表中可以看出，DNS模擬得到的St與實驗結(jié)果最為接近。這也意味著對于方柱繞流（Re=10 000）這類復(fù)雜流動，DNS模擬最為準(zhǔn)確。

表2 不同計算方法得到的StTab.2 St computed by different methods

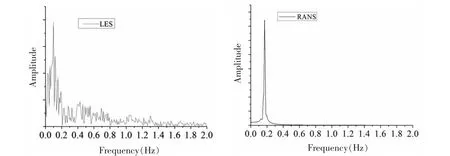
圖17 LES和RANS計算得到的升力系數(shù)頻譜圖Fig.17 The corresponding frequency spectrum of lift coefficient computed by LES and RANS

5 結(jié) 論

本文通過自主設(shè)計和編制的DNS并行計算程序，在“神威·太湖之光”超級計算機(jī)上，開展了中等雷諾數(shù)二維方柱繞流的DNS模擬研究。通過對流動中渦系發(fā)展及演化過程的分析，以及與RANS和LES模擬結(jié)果的對比分析，可以得出以下結(jié)論：

（1）通過低雷諾數(shù)（Re=100）方柱繞流DNS模擬及時空分辨率收斂性分析可知，計算程序的設(shè)計編制是正確的，且在滿足DNS要求的時空分辨率情況下，計算結(jié)果準(zhǔn)確可靠；

（2）對于中等雷諾數(shù)（Re=10 000）方柱繞流，本文的DNS模擬成功地捕捉到鈍體繞流的典型流動現(xiàn)象和特征，如：渦街的形成和脫落，分離泡的產(chǎn)生和變化，偽三角區(qū)的形成，一些特有的穩(wěn)定流場結(jié)構(gòu)如單極子型渦與偶極子型渦的形成和遷移，以及小尺度渦的耗散等；同時，對于方柱尾流場特征及渦系結(jié)構(gòu)的模擬結(jié)果，與公開發(fā)表文獻(xiàn)的結(jié)果基本一致；

（3）與RANS和LES的中等雷諾數(shù)（Re=10 000）方柱繞流模擬結(jié)果相比，無論是流場特征、渦系結(jié)構(gòu)等流動細(xì)節(jié)，還是方柱升力系數(shù)時歷和主渦脫落頻率（St）等宏觀量，DNS模擬結(jié)果都明顯更為準(zhǔn)確，體現(xiàn)了DNS在復(fù)雜精細(xì)流場模擬方面的優(yōu)勢。

致謝：本文的研究工作得到了中國船舶科學(xué)研究中心張楠研究員的大力幫助和啟發(fā)性指導(dǎo)，以及江南計算技術(shù)研究所的徐占工程師、陳德訓(xùn)高工、劉鑫高工等人的技術(shù)支持。對于他們的無私幫助和對論文的貢獻(xiàn)，作者在此表示由衷的感謝！