夾芯結構的疲勞裂紋損傷擴展研究

羅白璐，朱英富，李之達，鄭紹文

（1.中國艦船設計研究中心，武漢430064；2.武漢理工大學，武漢430063）

0 引 言

復合材料疲勞損傷演化規律及作用機理的研究，對于材料的疲勞力學研究有著很重要的意義。Mao[1]依照材料的疲勞損傷演化會經歷三個階段，基于唯象角度標示出了循環次數和復合材料整體損傷之間的關系。Montesano[2]指出在疲勞損傷的過程中應該注重有可能會發生的局部應力重分配情況，導致疲勞累積損傷演化。Singh[3]基于能量角度，選用雙參數威布爾分布，將所研究的復合材料的臨界能量釋放率進行了定義，并對可能發生的數值波動進行統計，通過建立損傷演化模型探討了在雙軸疲勞載荷情況下碳纖維和玻璃纖維的損傷演化過程和應力-應變等關系。

本文應用累積損傷力學理論，以夾芯復合材料板為研究對象，開展了復合材料在交變載荷下疲勞累積過程的演化規律研究，借助于能敏感反映復合材料性能的剛度量，建立了夾芯復合材料結構在彎曲交變載荷作用下的結構疲勞累積損傷漸降模型。對全壽期內裂紋的萌生及擴展的全歷程規律進行了描述，并采用剛度衰減作為復合材料結構失效狀態控制量，最終構建了一個含疲勞全過程分析的宏觀唯象損傷模型。

1 累積損傷分析

在應變以及應力的作用下，在某一點或者是某些點的地方會出現一些永久性的變化，而這些變化會隨著循環次數的增多發生進一步的擴大，最終導致材料發生累計損傷。在材料的前期其內部會出現大量的裂紋，當裂紋的數量達到一定的程度以后就會有斷裂的情況發生。然而，當材料到了其壽命后期的時候，此時因為材料累積了大量的來自于各方面的損傷，促使裂紋發生快速的擴散，在宏觀上表現出材料突然的斷裂。如圖1所示。

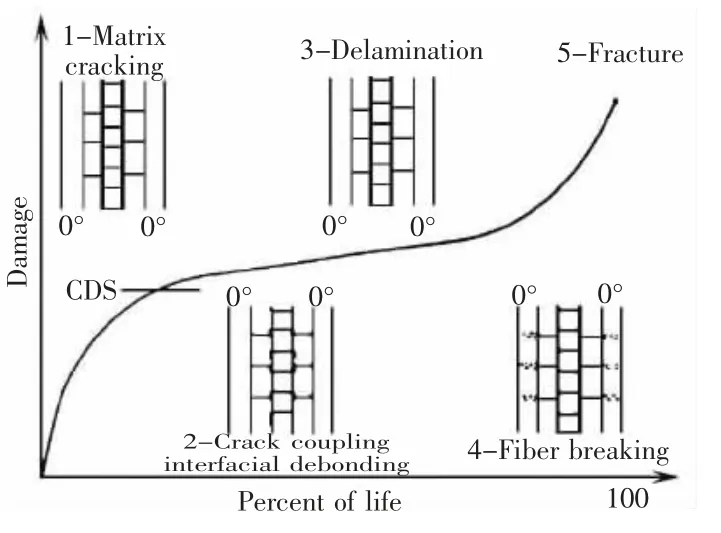
圖1 復合材料疲勞損傷演化規律Fig.1 Evolution rule of fatigue damage of composite materials

若將l1表示為損傷標量的彈性模量減少

因此復合材料結構的損傷變量D可做如下定義：

式中：D（n）表示加載n次后的結構損傷量；E（0）表示復合材料的初始彈性模量；E（n）表示加載n次后材料的剩余彈性模量。

如果材料發生疲勞斷裂時，即復合材料的剛度為E（）

N時：

2 損傷過程中材料性能退化

受疲勞加載的影響，隨著加載循環次數的逐漸增加，局部區域的材料性能會出現突降，外在的主要表現體現為材料剛度的下降，而這與該區域結構的應力狀態無關。因此，我們在材料的衰變過程中，采用剩余剛度的方法來考核和預測復合材料的疲勞壽命。本文定義循環n次下材料的切線剛度為E（n），稱之為剩余剛度，以便描述材料的疲勞損傷程度。

根據Yang[4]等人所提出的剩余剛度退化公式

式中：n表示載荷加載的循環次數；E（）0代表其初始剛度。

在疲勞循環作用下，由于復合材料的循環次數和剛度呈反比例關系，因此上式中Qv＞0。

將（4）式從n1到n2進行積分，可得

當n1=0，n2=n時，可以將（5）式轉化成為：

當n=N時，N表示材料的疲勞壽命，（6）式進一步轉化為：

因此，變量Q表示為：

而在（8）式中代入（6）式可得下式：

結合Lee[5]提出的剩余剛度與強度的關系表達式

式中：σU為結構的靜極限強度；σ為所施加的疲勞應力值；c1及c2為試驗模型常數，且c1≥1，c2＞0。

（10）式可轉化為

將其代入到上述剩余剛度退化模型（9）式中得

式中：V代表與疲勞載荷應力相關的線性函數，可表示為V=a+bσ，a及b為試驗系數。

因此，剩余剛度模型可進一步轉化為

3 試驗研究

3.1 試驗對象

取常幅載荷疲勞試驗在5個應力水平下進行，每個應力水平下取3個試件為實驗對象來考察夾芯復合材料結構在常幅載荷下的彎曲疲勞行為。試件外觀尺寸如圖2所示。

圖2 試件尺寸Fig.2 Specimen size

3.2 試驗方法及條件

考慮到除了遭遇主機振動的局部高頻載荷影響的構件外，承受艦船正常使用中的波浪交變載荷譜的船舶結構，經常使用的是104～106次循環范圍內的疲勞壽命曲線。因此，本文將到達106次循環而未發生破壞作為整個結構失效的條件疲勞極限。

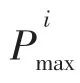
圖3 三點彎曲疲勞加載圖Fig.3 Diagram of three-point bending loading

表1 疲勞試件編號Tab.1 Serial number of fatigue specimen

3.3 試驗結果

圖4 疲勞荷載取45%Pmax時試件損傷圖（a1，a2為疲勞裂紋）Fig.4 Damage state at 45%Pmax fatigue loads(a1,a2 represent fatigue cracks)

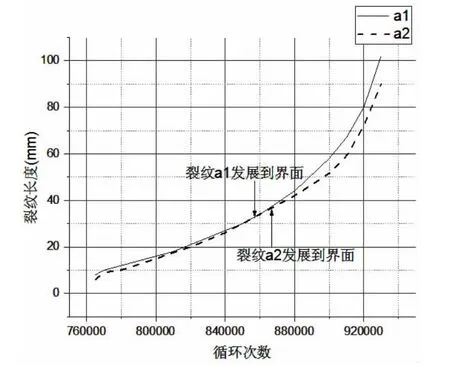
圖5 疲勞荷載取45%Pmax時試件裂紋擴展圖Fig.5 Crack propagation curve at 45%Pmax fatigue loads

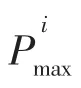
這些試件的疲勞損傷圖均反映出，在疲勞載荷作用下，夾芯復合材料板的初始破壞區域均為中間芯材層的泡沫內。隨著循環次數增加，多條貫穿泡沫芯材的裂紋會沿著纖維與芯材的界面層繼續擴展，直至泡沫與纖維層完全分離。當芯材層的裂紋擴展至纖維界面的裂紋擴展時，當泡沫與纖維層完全脫離，此時試件的整體剛度急劇下降，試件也很快發生破壞。

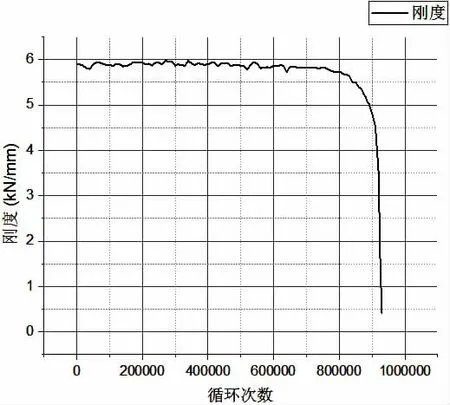
圖6 疲勞荷載取45%Pmax時試件剛度曲線Fig.6 Stiffness curve at 45%Pmax fatigue loads

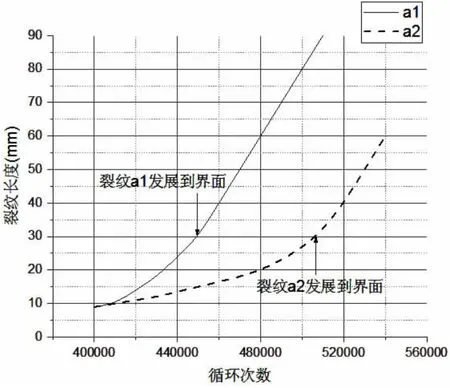
圖8 疲勞荷載取50%Pmax時試件裂紋擴展圖Fig.8 Crack propagation curve at 50%Pmax fatigue loads

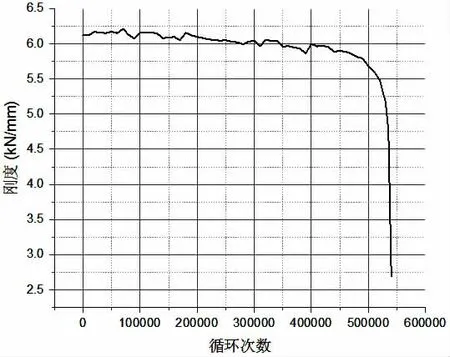
圖9 疲勞荷載取50%Pmax時試件剛度曲線Fig.9 Stiffness curve at 50%Pmax fatigue loads

圖10 疲勞荷載取55%Pmax時試件損傷圖Fig.10 Damage state at 55%Pmax fatigue loads(‘a’represents fatigue crack)

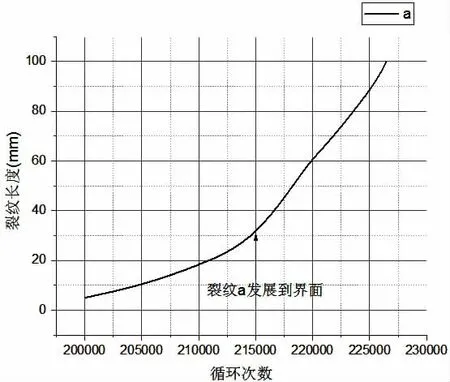
圖11 疲勞荷載取55%Pmax時試件裂紋擴展圖Fig.11 Crack propagation curve at 55%Pmax fatigue loads

我們可以將試件在泡沫芯子內的裂紋萌生擴展定義為第一階段微裂紋擴展，而裂紋在纖維與芯子界面的擴展定義為第二階段斷裂裂紋擴展。無論在何種疲勞應力水平下，第一階段的裂紋擴展都占了試件全壽命的絕大部分時間，第二階段的擴展過程不僅迅速且無任何征兆的結束，直接破壞，整體過程呈現明顯的脆性破壞特征。

圖12 疲勞荷載取55%Pmax時試件剛度曲線Fig.12 Stiffness curve at 55%Pmax fatigue loads

圖13 疲勞荷載取60%Pmax時試件損傷圖Fig.13 Damage state at 60%Pmax fatigue loads(‘a’represents fatigue crack)

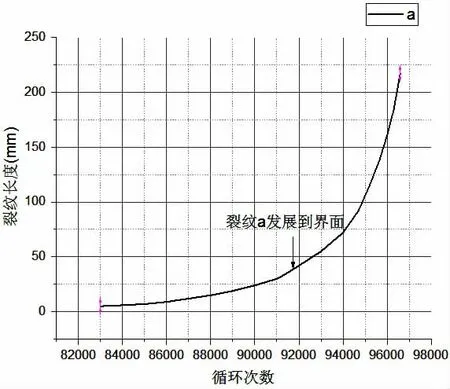
圖14 疲勞荷載取60%Pmax時試件裂紋擴展圖Fig.14 Crack propagation curve at 60%Pmax fatigue loads

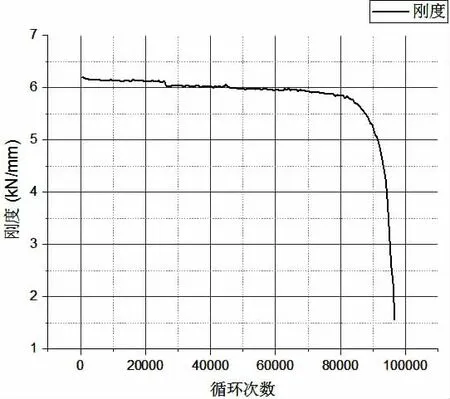
圖15 疲勞荷載取60%Pmax時試件剛度曲線Fig.15 Stiffness curve at 60%Pmax fatigue loads

在這兩個顯著的失效擴展階段，由試件的剛度曲線圖可以看出，在第一個微裂紋的萌生和擴展階段，試件剛度緩慢下降；第二個斷裂裂紋快速擴展階段，試件剛度劇烈下降。剛度緩慢下降段可以被看成是損傷的增長段，這個階段基本上占了試件壽命的90%。剛度的劇烈變化段可以看作是破壞的產生與發展階段，試件的損傷發展到一定程度后，當出現大的貫通芯材的裂紋或是芯材滑移，直至無法滿足試件承載力的要求時，試件最終完全失效破壞。

表2 60%Pmax應力水平下試件的剩余剛度（kN/mm）Tab.2 Residual stiffness at 60%Pmax fatigue load(kN/mm）

表3 55%Pmax應力水平下試件的剩余剛度（kN/mm）Tab.3 Residual stiffness at 55%Pmax fatigue load(kN/mm）

表4 50%Pmax應力水平下試件的剩余剛度（kN/mm）Tab.4 Residual stiffness at 50%Pmax fatigue load(kN/mm）

表5 45%Pmax應力水平下試件的剩余剛度（kN/mm）Tab.5 Residual stiffness at 45%Pmax fatigue load(kN/mm）

表6 40%Pmax應力水平下試件的剩余剛度（kN/mm）Tab.6 Residual stiffness at 40%Pmax fatigue load(kN/mm）

夾芯復合材料板在彎曲疲勞試驗的循環加載過程中，各疲勞應力水平下的剩余剛度試驗數據見表2-6。

結合表4，以50%Pmax疲勞載荷應力水平為對象，將試件的剩余剛度和初始剛度之比E（n）/E（0）為縱坐標，循環次數n與50%Pmax應力水平下的疲勞壽命N之比為橫坐標，繪成如圖16的夾芯復合材料板彎曲疲勞剩余剛度退化曲線。

從圖16可以看出在未完全失效前，剩余剛度退化率非常緩慢，僅在臨界失效段才出現快速“斷崖式”的下降。根據以上退化趨勢，結合剩余剛度退化模型，使用最小二乘法進行數值擬合，得到剩余剛度退化模型中的參數C1=1.018，C2=0.698，a=0.657，b=1.861，最終代入（13）式，得到夾芯復合材料板的彎曲剩余剛度退化模型：

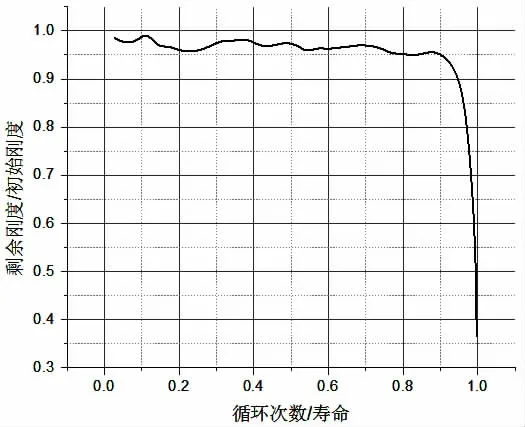
圖16 夾芯復合材料板彎曲疲勞剩余剛度退化曲線Fig.16 Residual stiffness degradation curve of sandwich composite plates

表7 60%Pmax應力水平下剩余剛度模型計算值與實測值對比Tab.7 Comparison of residual stiffness values between calculation and measured fatigue load at 60%Pmax

續表7

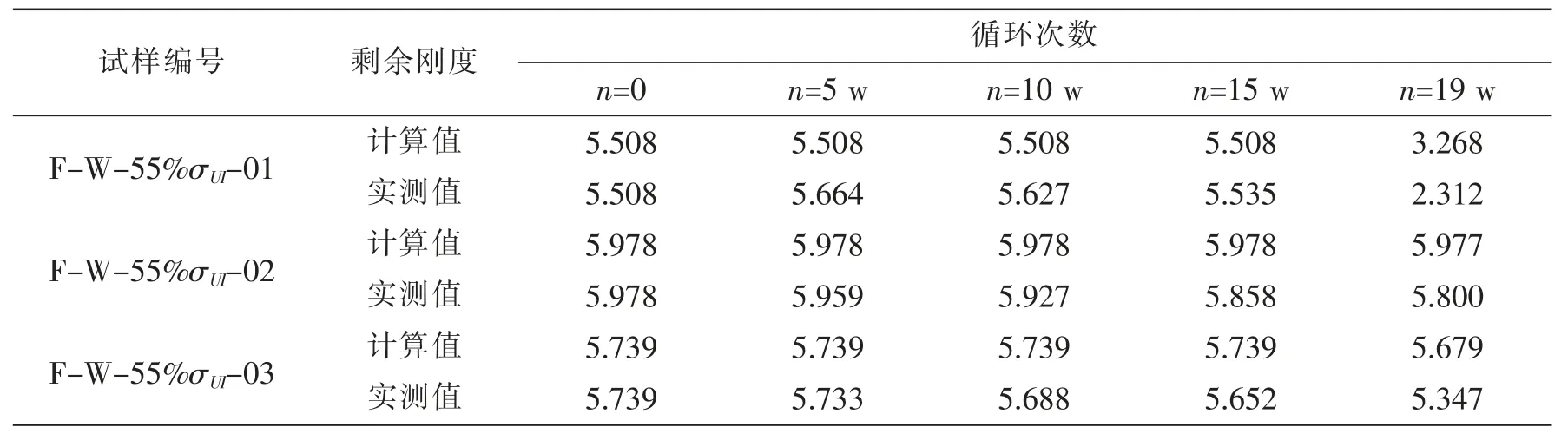
表8 55%Pmax應力水平下剩余剛度模型計算值與實測值對比Tab.8 Comparison of residual stiffness values between calculation and measured fatigue load at 55%Pmax

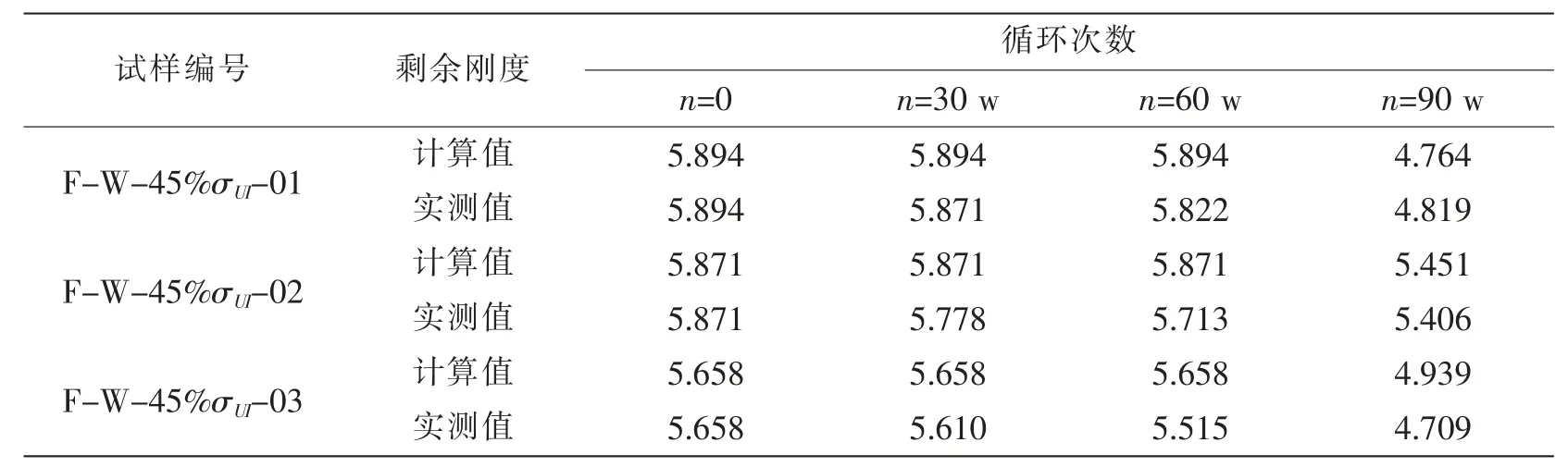
表9 45%Pmax應力水平下剩余剛度模型計算值與實測值對比Tab.9 Comparison of residual stiffness values between calculation and measured fatigue load at 45%Pmax

表10 40%Pmax應力水平下剩余剛度模型計算值與實測值對比Tab.10 Comparison of residual stiffness values between calculation and measured fatigue load at 40%Pmax

利用上式計算其他各應力水平下試件各階段的剩余剛度值，對比各階段的實測值見表7-10。

上述計算值與實測值對比分析可以看出，（14）式擬合的剩余剛度退化模型的適用性較好，在不同應力水平60%Pmax，50%Pmax，45%Pmax和40%Pmax下，階段性的剩余剛度退化值預測的一致性均較好。

4 結 論

（1）在疲勞典型失效特征方面，試驗結果表明，作為孔穴材料的芯材，在循環載荷作用下易被粉碎（壓實），導致彎曲試件橫截面上的中性層偏移。因此當加載卸載交替進行時，伴隨著宏觀剛度的下降，使得芯材開始沿第一主平面撕裂，并緩慢擴展。當這個漫長階段結束，即芯材中裂紋擴展至蒙皮時，裂紋開始沿芯材與蒙皮間界面快速擴展，芯材與蒙皮層合板之間完全分離，試件剛度呈現“斷崖式”下降，隨之試件喪失承載力并最終破壞。

（2）夾芯復合材料結構在承受疲勞載荷作用時，材料內部會產生多種損傷形式，在宏觀上的表現為材料力學性能的衰減，且衰減程度與加載次數間為非線性關系。本文在研究了復合材料疲勞損傷與其剛度衰減間的相互聯系的基礎上，提出損傷擴展速率統一的“緩→快”型變化趨勢，并基于此建立了描述材料損傷演化的宏觀唯象損傷模型，全面反映了復合材料全壽命階段內的損傷演化歷程。

（3）從裂紋的擴展延伸特征及與試件剛度的變化過程進行對比分析后可看出，不論施加的交變應力水平的大小如何，夾芯復合材料結構中的裂紋擴展均呈現明顯的兩個階段。第一階段，泡沫芯子內微裂紋萌生與緩慢擴展，試件剛度緩慢變化，整個歷程約占試件全壽期90%的時間；第二階段，芯子與纖維層界面層的裂紋快速貫穿擴展，試件剛度驟降式下降，整個歷程約占試件全壽期10%的時間。