基于Narx網絡模型的系泊纜截斷點運動計算

張隆輝，劉正鋒，魏納新，匡曉峰，范亞麗

（中國船舶科學研究中心，江蘇 無錫214082）

0 引 言

受限于試驗水池的大小以及模型尺度的選擇，要將深水系泊系統按合適的尺比完整地布置于水池中是非常困難的，而擴建更大更深的試驗水池無疑需要更高的代價。目前，一般采用被動式截斷試驗技術的方式進行大水深情況下的系泊系統模型試驗。但被動式截斷技術不能很好地實現對全水深系統下的動力相似，有時實現完全的靜力相似也十分困難，因此有些學者開始將研究方向轉向主動式截斷混合模型試驗技術[1-4]。

主動式截斷混合模型試驗技術（下簡稱主動式技術）是解決深水系泊模型試驗的一種新方法。所謂主動式技術，即將系泊纜進行截斷的情況下，使用伺服機構控制系泊纜截斷點處的運動，實現截斷的系泊纜與全水深下的系泊纜高度的動力相似，從而達到模擬全水深情況下系泊纜運動的目的。主動式技術的基本原理如圖1所示，通過安裝于平臺模型上的傳感器測得平臺的實時運動情況，然后在計算機中利用相關的數值方法如集中質量法、有限元方法等實時計算得到截斷點處的運動時歷，從而發出控制指令控制伺服機構進行運動。

圖1 主動式技術基本原理圖Fig.1 Schematic diagram of active truncated system

然而，如集中質量法等數值方法，由于系泊纜運動問題的強非線性特征，在每個時間步內都需要進行迭代求解，十分耗時。同時，由于這些數值方法對時間步長的選取存在要求，在復雜的試驗環境下，使用不恰當的時間步長可能出現迭代計算的不收斂；即使采用變步長的方式進行求解，其計算時間也會增加，因此通過計算機實時解算的方式并不十分可靠。

針對傳統數值方法存在的一些缺陷，本文提出了一種基于Narx神經網絡模型代替傳統的纜索動力學數值計算過程（流程簡圖對比見圖2），該方法通過網絡模型建立了平臺模型導纜孔處加速度與纜索截斷點處加速度之間的映射關系，因此將傳感器測得的水面平臺模型導纜孔處的加速度信息輸入網絡，即可輸出得到纜索截斷點處加速度值。該方法與傳統數值方法相比計算耗時更少、更為穩定，并具有較好的精度。

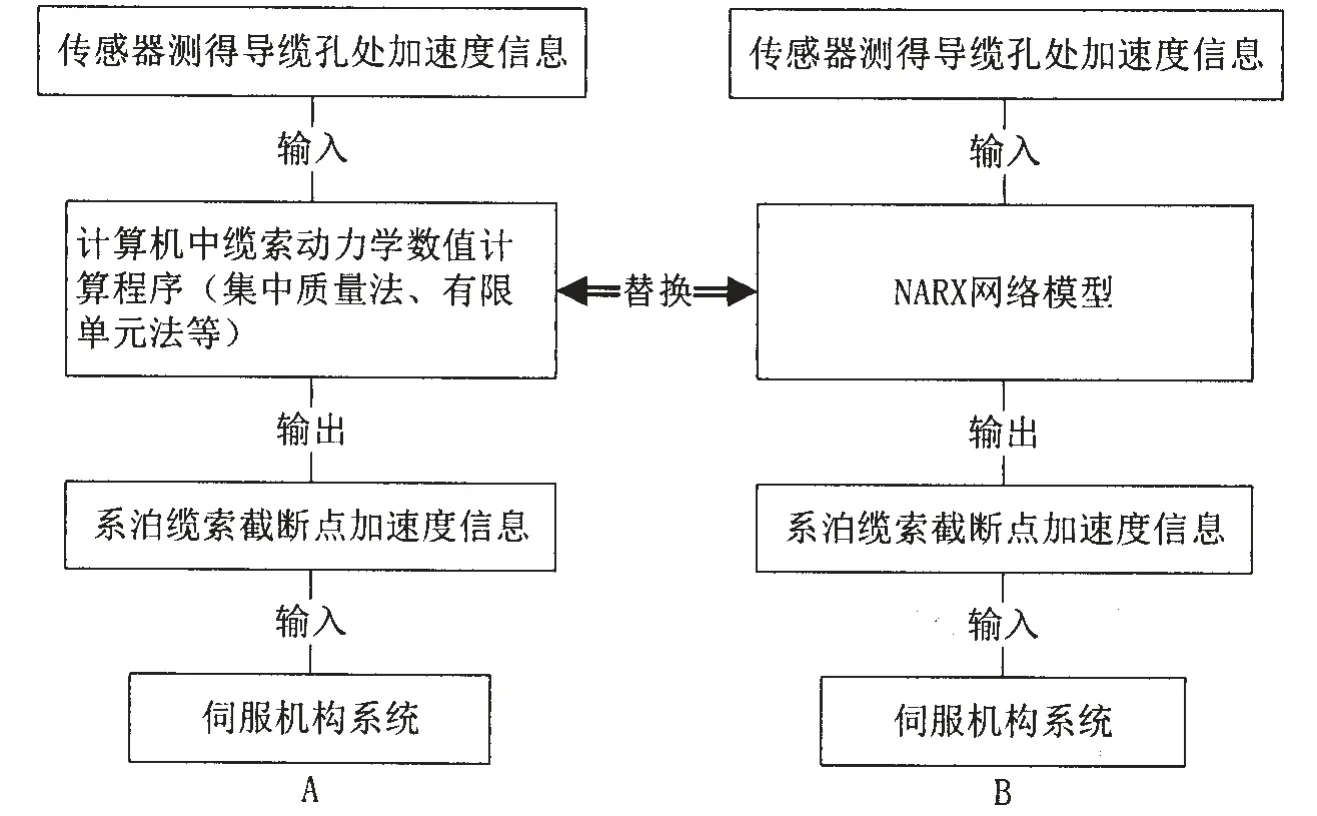
圖2 執行流程簡圖Fig.2 Flow diagram of active truncated system

1 Narx神經網絡

神經網絡技術作為20世紀末迅速發展起來的一門技術，由于其良好的非線性映射能力、自學習適應能力和并行處理信息的能力，為解決未知不確定非線性系統辨識問題提供了一條新思路[5]。根據應用場合的不同，神經網絡可以分為靜態神經網絡和動態神經網絡兩類。靜態神經網絡沒有反饋成分，也不包含輸入延時，輸出直接由輸入通過前向網絡算出；動態神經網絡的輸出不僅依賴于當前輸入，還與當前和過去的輸入、輸出有關。因此在非線性系統辨識問題中通常采用動態神經網絡[6]。Narx網絡是一種由靜態神經元和網絡輸出反饋構成的動態神經網絡，已經有學者證實該網絡十分適合對非線性系統的建模[7]。近年來，Narx網絡亦被廣泛地應用于解決海洋平臺運動預報及其系泊系統張力預報的問題中，如Guarize等人[8]將Narx網絡應用于某FPSO的運動與系泊系統的張力預報，通過將有限元方法計算得到的FPSO運動時歷作為訓練數據代入創建的Narx網絡進行訓練，再利用訓練好的網絡預報得到FPSO的運動以及系泊系統導纜孔處的張力時歷；Uddin等人[9]則將Narx網絡應用于SPAR平臺運動及其系泊系統的張力預報中，同樣也獲得了良好的預報結果；Christiansen等人[10]則將Narx網絡應用于系泊系統的疲勞分析問題，認為由于訓練完成的網絡的計算速度遠遠快于一般有限元程序的計算速度，因此能夠極大地縮短疲勞分析的時間，同時他們還對使用不同的誤差函數情況下的Narx網絡性能進行了比較與討論。此外還有許多的研究工作證明Narx網絡適用于解決海洋平臺及其系泊系統的相關問題[11-13]，在此不一一贅述，但大部分的研究工作都主要關注系泊纜索導纜孔處的運動及其受力情況，還未有相關工作將Narx網絡應用于系泊纜索截斷點處的運動分析，本文的工作即著眼于此。

Narx網絡模型的基本結構如圖3所示，其模型表示方程為：

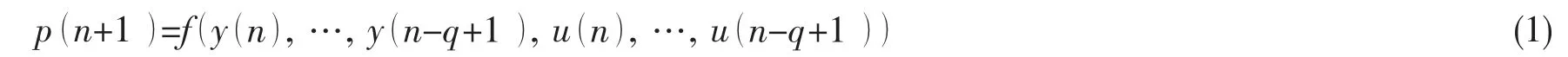
其中：q為延遲階數，即在第n+1時刻，系統的輸出取決于輸入的q個過去值和輸出的q個過去值；p（n+1）表示實際輸出y（n+1）的估計值；f（·）表示多層感知器所實現的非線性函數；e （n+1）表示估計值的誤差，用于網絡中感知器權值的修正，修正算法主要有分時段訓練算法以及連續訓練算法兩種方式[14]。

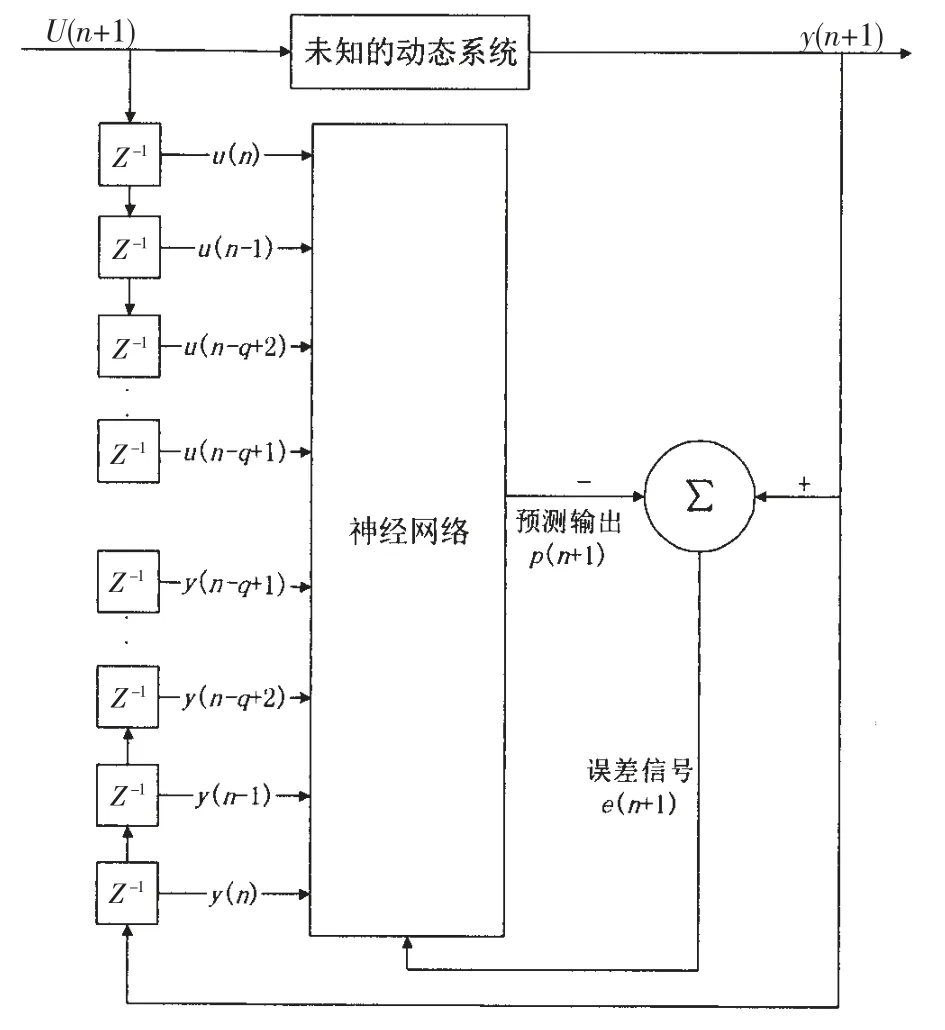
圖3 Narx網絡基本結構圖Fig.3 Basic structure of Narx network

圖3中的未知動態系統即本文中基于集中質量法的纜索動力學問題模型，該模型最早由Walton等人[15]提出，并被廣泛地應用于系泊問題的計算。在集中質量法模型中，通過輸入纜索上端的運動邊界條件信息，即可計算得到截斷點處的運動解。創建Narx網絡的目的，即辨識原有基于集中質量法的復雜纜索動力學模型，將其表示為如（1）式所表示的更為簡單的形式。辨識后所得到的模型由于不再需要進行迭代求解，提高了求解速度，因此較使用集中質量法進行實時數值求解的方式更適用于截斷點運動實時控制。

2 Narx網絡模型的建立與訓練

2.1 數據準備

針對某工作于320 m水深的半潛平臺及其系泊系統模型（縮尺比為1：50，平臺系泊系統布置圖見圖4），取四根系泊纜中的一號纜進行分析，計算三種不同工況下一號纜截斷點的運動情況。截斷點位置在考慮水池深度及其它條件需要下，取纜長為4 m的位置。相關模型參數及工況條件可見表1到表3。

表1 半潛平臺模型參數（1:50）Tab.1 Principal dimensions of the semisubmerged platform model

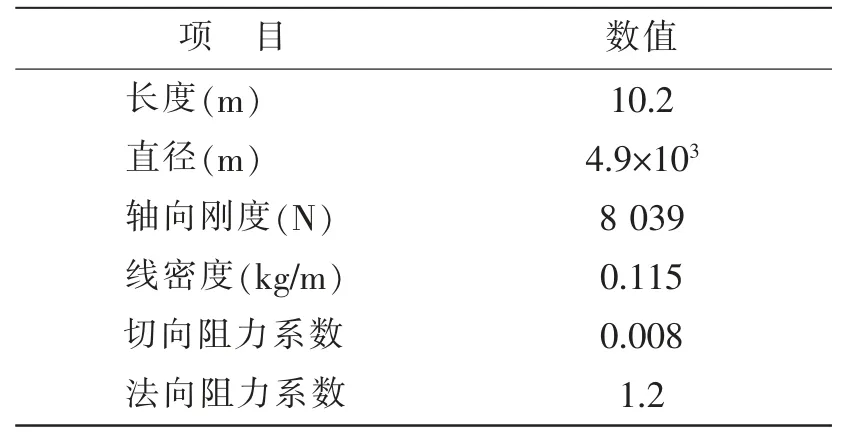
表2 系泊系統模型參數（1:50）Tab.2 Parameters of the mooring system model

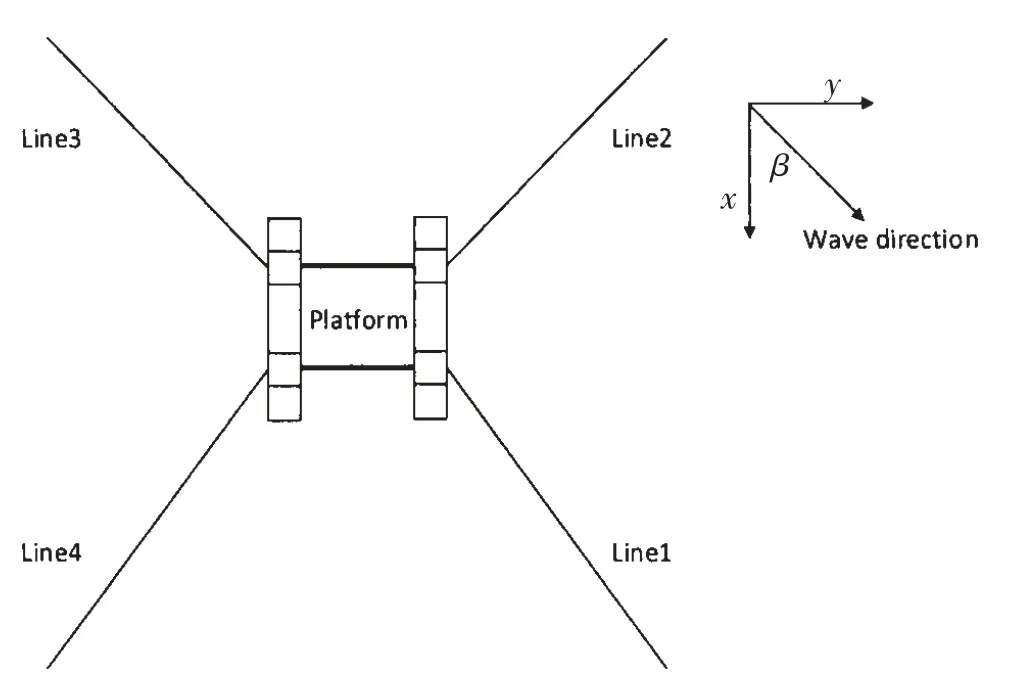
圖4 平臺系泊系統模型布置圖Fig.4 Layout of mooring system

表3 工況海浪譜參數（1:50）Tab.3 Metocean environmental cases

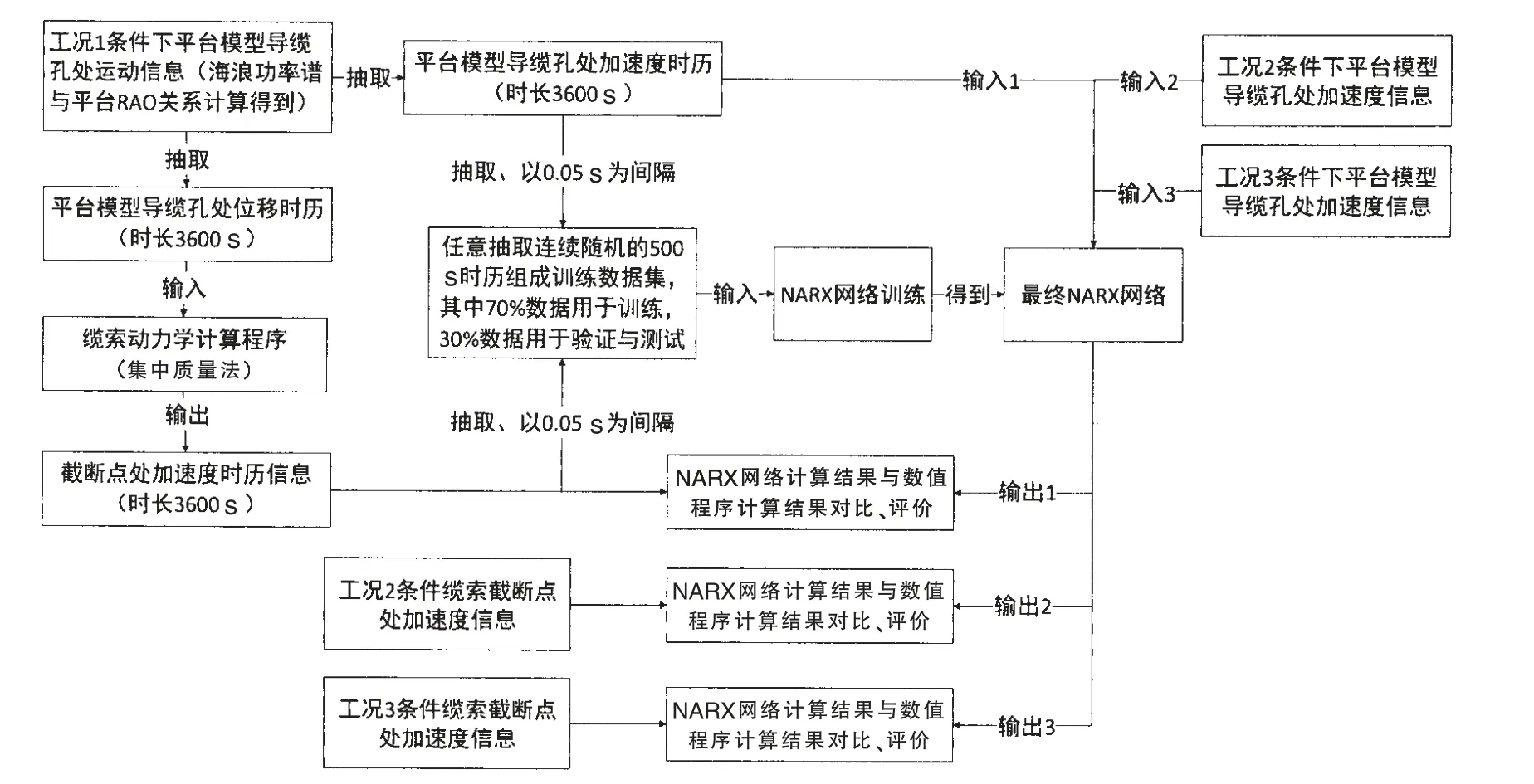
圖5 數據準備及分析流程圖Fig.5 Data preparation and analysis flow diagram

為確定網絡的權值，需要相應的數據集對網絡進行離線訓練。創建Narx網絡的目的在于替代相關數值程序完成計算纜索動力學問題的任務，因此數據集中平臺導纜孔及纜索截斷點處的加速度時歷信息可以通過相應的數值程序計算得到。本文數據集中導纜孔處的加速度信息通過平臺RAO與海浪譜間的關系轉換計算得到，而后將導纜孔處的運動信息作為邊界條件代入纜索集中質量法進行動力學計算，得到纜索截斷點處的加速度值。如圖5所示，三個工況中取工況1為網絡訓練數據集的來源，工況2和工況3則是為了檢驗網絡的泛化能力（即為說明同一網絡也可以適用于不同工況）而設置。計算結果數據的總時長為3 600 s，其中的500 s用于網絡的訓練，剩余的3 100 s則用于檢驗網絡的預報能力。考慮系統通信及試驗采樣要求需要，取相鄰時間間隔Δt為0.05 s。這里的Δt并非集中質量法的計算時間步長，而是截取運動時歷信息的時間間隔Δt，本文中集中質量法的計算步長則是取0.01 s，每根纜單元數取204個。

2.2 網絡的建立與訓練

本文利用Matlab中的神經網絡工具箱，創建相應的Narx網絡。一般而言，延時階數與神經元數取越大越好，然而這樣訓練過程的計算量亦會增加。根據計算機的硬件配置以及問題的需要，這里根據試湊法選取了延遲階數為35，神經元的個數則根據（2）式所示的經驗公式[16]確定為16：

其中：l為隱含層神經元數；m為輸入層節點數；n為輸出層節點數；a為1-10間的常數。

網絡的權值調整算法使用貝葉斯正則化反向傳播算法，使用該訓練算法被證實可以使得創建好的Narx網絡具有良好的泛化能力[17-19]，創建好的Narx網絡結構形式如圖6所示。

圖6 創建的Narx網絡結構圖Fig.6 Structure of Narx network

如圖5所述，取工況1數據集（500 s）中前70%的數據作為訓練集，15%的數據作為驗證集，15%的數據作為測試集對網絡進行訓練。將訓練完成后的Narx網絡命名為NET_0.12_2.15，其中0.12表示有義波高值，2.15表示譜峰周期值。工況1導纜孔處的三個方向加速度功率譜密度見圖7。

2.3 仿真計算結果與分析

將訓練好的網絡NET_0.12_2.15用于計算工況1情況下時長為3 600 s的截斷點加速度時歷信息。在理想的情況下，網絡的計算結果應該與集中質量法計算的結果非常吻合。網絡的計算結果與集中質量法的計算結果對比見下圖8～9及表4（圖8（a）-（c）僅截取3 000-3 050 s內的計算結果）。

圖7 工況1導纜孔x，y，z方向加速度功率譜密度Fig.7 Spectral density of acceleration of fairlead in case 1

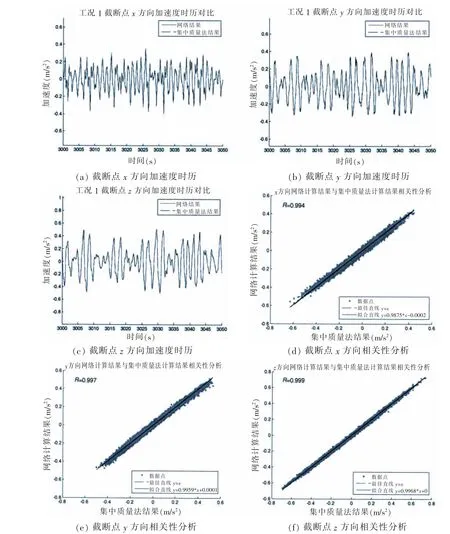
圖8 工況1截斷點加速度時歷對比Fig.8 Time history of acceleration of truncated point in case 1

從表4中可以看出，NET_0.12_2.15的計算結果與集中質量法計算得到的結果在峰值處存在較大的偏差，但在可接受的范圍內；同時由圖8與圖9可以看出兩者在時頻域內的結果是相符的。圖8（d）-（f）為三個方向的集中質量法計算結果與網絡計算結果的相關性分析，R值的大小則反映了集中質量法計算結果與網絡計算結果的線性相關性程度（最大值為1，最小值為0）。三個方向的R值分別為0.994，0.997，0.999，且擬合直線非常接近于最佳直線y=x，說明網絡計算結果與集中質量法計算結果具有很強的線性相關性，網絡計算結果與集中質量計算結果基本相符。由此，將NET_0.12_2.15替代集中質量法程序進行工況1條件下截斷點處的加速度時歷計算是可行的。更進一步地，為了說明訓練好的NET_0.12_2.15網絡不僅適用于工況1條件下的計算，同時也適用于其它工況條件下的計算，設置了工況2，3檢驗網絡NET_0.12_2.15的推廣性能。NET_0.12_2.15在工況2，3條件下的計算結果可見圖10～13及表5和表6。

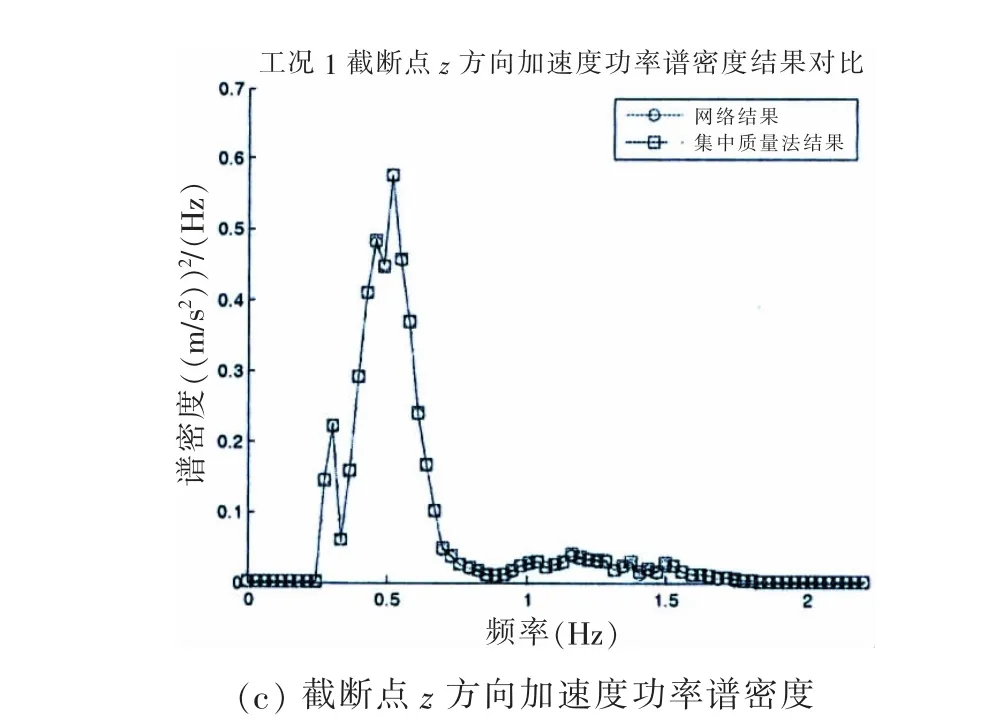
圖9 工況1截斷點加速度功率密度結果對比Fig.9 Spectral density of acceleration of truncated point in case 1

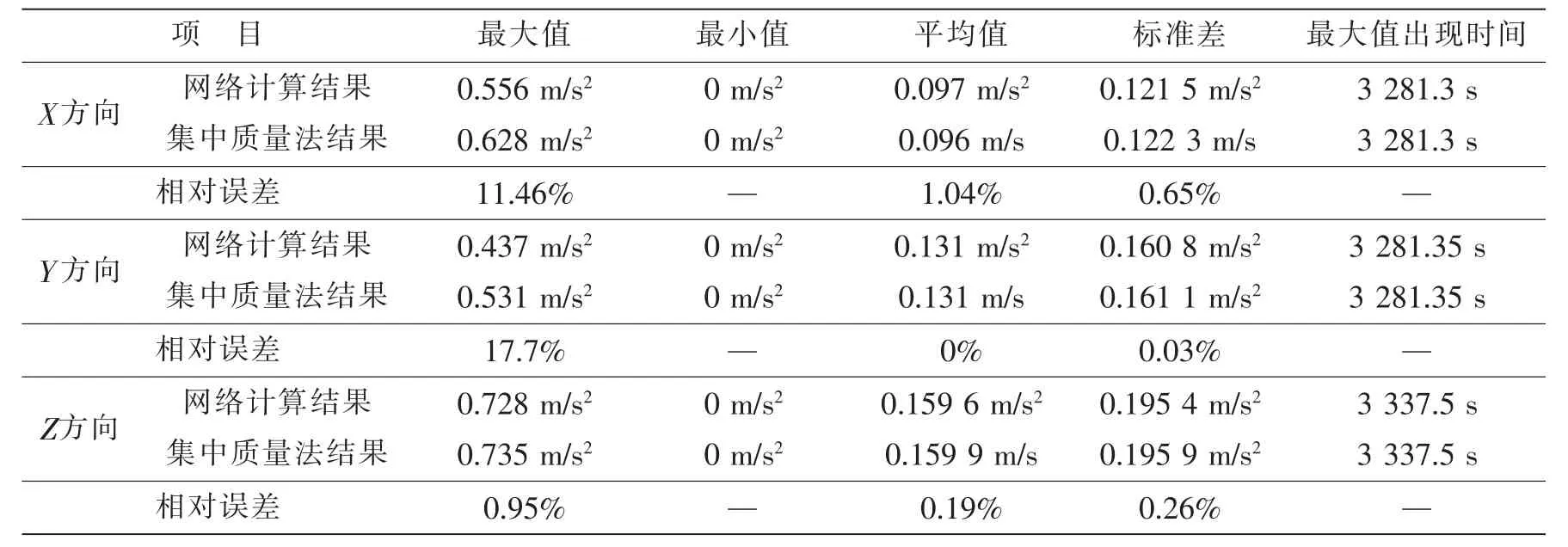
表4 工況1加速度結果對比Tab.4 Comparison of results of Narx networks and lumped massed method in case 1

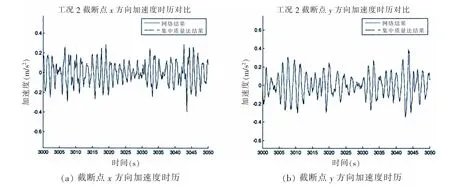
圖10 工況2截斷點加速度時歷對比Fig.10 Time history of acceleration of truncated point in case 2

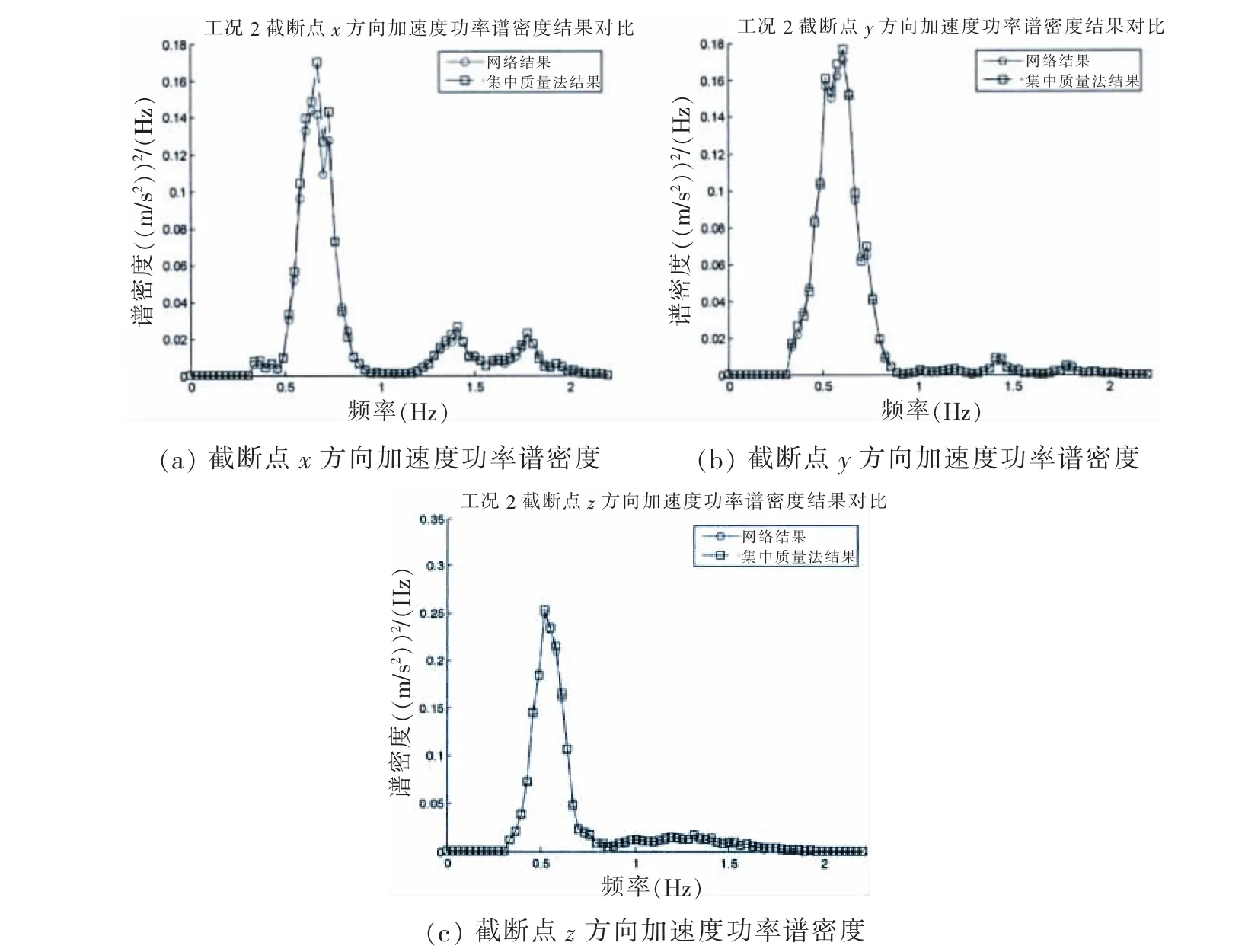
圖11 工況2截斷點加速度功率密度結果對比Fig.11 Spectral density of acceleration of truncated point in case 2

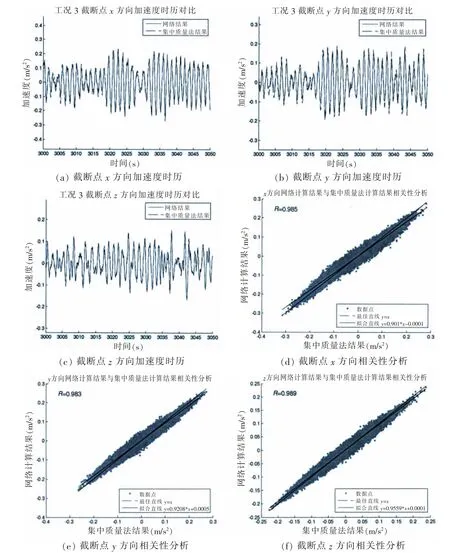
圖12 工況3截斷點加速度時歷對比Fig.12 Time history of acceleration of truncated point in case 3

圖13 工況3截斷點加速度功率密度結果對比Fig.13 Spectral density of acceleration of truncated point in case 3

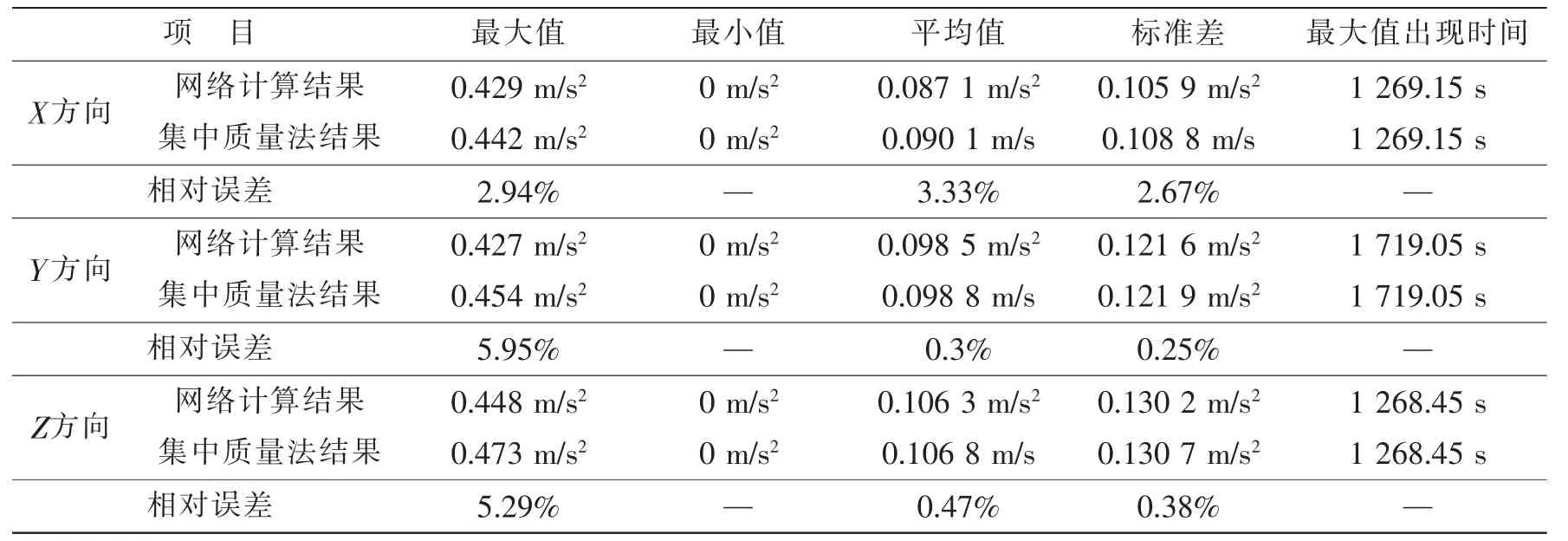
表5 工況2加速度結果對比Tab.5 Comparison of results of Narx networks and lumped massed method in case 2

表6 工況3加速度結果對比Tab.6 Comparison of results of Narx networks and lumped massed method in case 3

從表5-6可以看到，在工況2，3條件下最大值的相對誤差較工況1情況下更小且對出現最大峰值的時間捕捉準確，但平均值及標準差的相對誤差有所增大，說明網絡NET_0.12_2.15的峰值計算結果較好，但均值與標準差的誤差增大則反映了在工況2，3條件下網絡的全局（3 600 s）計算精度有所下降。全局計算精度的下降也可以由圖10（d）-（f）和圖12（d）-（f）看出，其反映為數據點更為分散，且擬合直線與最佳直線出現了較大的偏移。總的來看，工況2，3條件下網絡的計算結果與集中質量法計算結果在時頻域內較為吻合，說明了NET_0.12_2.15不僅適用于工況1條件下的計算，同時也適用于工況2，3條件下的截斷點加速度時歷計算。

3 結 論

（1）文中基于Narx網絡模型所創建網絡NET_0.12_2.15的訓練數據集僅依賴于工況1條件下集中質量法的計算結果，但在工況2，3條件下其計算結果也與集中質量法計算結果基本吻合，說明基于Narx網絡模型的方法具有較好的泛化能力。

（2）Narx網絡模型與集中質量法等數值計算程序相比，其計算時間更短（在i5、6 GB的筆記本電腦上的計算時間只需要0.01 s到0.02 s每個時間步長），且在實際應用中可以以固定的時間步長進行計算，因此十分適用于主動式技術中實時計算的要求。

（3）Narx網絡模型在本文中可以很好地實現截斷點與導纜孔間的加速度映射關系建模，同樣該模型也適用于截斷點與導纜孔間位移-位移關系、速度-速度關系的建模。但在實際應用中，以加速度關系最為方便，因限于篇幅，本文中僅列舉加速度關系進行說明。

（4）Narx網絡的計算結果較一般數值方法結果而言整體數值略偏小，由此將其代替一般數值方法進行纜索運動計算及控制，從而造成對系泊纜索張力的影響，需要在后續的工作中繼續研究。