基于競爭蛙跳算法的聯合火力打擊任務規劃方法

王海峰,高小軍,劉 昊

(1.中國人民解放軍31696部隊,遼寧 錦州 121000;2.鄭州聯勤保障中心,河南 鄭州 450000)

聯合火力打擊是未來聯合作戰的重要環節,對聯合火力打擊任務規劃的綜合效果評估和優化是聯合作戰籌劃中的工作重點和難點[1]。考慮到聯合火力打擊任務規劃中涉及的火力打擊兵器種類、彈藥類型和目標數量繁多,問題復雜度遠高于過往戰爭形態中以單一兵種的動態火力分配問題,手工作業手段難以應對,必須考慮引入智能優化算法求解聯合火力打擊任務規劃問題。聯合火力打擊任務規劃中的兵力、火力、目標分配問題在軍事運籌領域屬于動態火力分配問題,以被證明屬于NP完全問題[2]。針對此類問題,國內外的學者已經進行了充分的研究和論證,隨著計算機運算能力的大幅提升和人工智能研究的逐步深入,運用智能優化算法通過多代迭代找到NP問題最優解成為解決此類問題的有效解法。

智能優化算法是20世紀70年代隨人工智能而興起的一類仿生算法,代表算法包括以模擬生物群落行為規律的蜂群算法[3]、蟻群算法[4]、蛙跳算法[5]、魚群算法[6]、螢火蟲算法[7]、布谷鳥算法[8]、粒子群算法[9]、細菌覓食算法[10]等;以模擬自然界規律的細胞膜優化算法[11]、模擬退火算法[12]、量子進化算法[13]等;以及模擬生物種群內部演化規律的遺傳算法[14]、貪心算法[15]等。上述智能優化算法各自的理論出發點均不相同,但算法設計存在共同點:一是設計可動態調整的智能體框架,結合具體問題的可行解建立一一對應的映射關系,將問題求解轉化為向量空間中找最佳位置向量;二是通過引入偽隨機數使智能體在向量空間中隨機游走或多代變異演化,使可行解無限逼近周邊最優;三是通過設定退出條件限制迭代次數,并輸出優化后的最優解作為時限內的可行解。相比于基于數學函數的線性規劃算法,智能優化算法具有非線性不連續、約束條件調整方便、最優解輸出可控等優點,然而算法也存在易陷入局部最優陷阱,以及收斂代數和優化效果不可控的風險。基于此,本文以蛙跳算法為標準,借鑒并引入遺傳算法中的壽終正寢和優勝劣汰機制,設計了競爭蛙跳算法,并將該算法引入聯合火力打擊任務規劃問題求解中,實現了動態火力分配的自動生成和智能優化,取得了良好的工程應用效果。

1 問題描述

聯合火力打擊任務規劃問題是在限定的兵力、火力和目標條件下,確保以完成火力打擊任務份額為前提,使我方兵力和火力損耗最小的動態兵力、火力、目標分配問題。設我方參與聯合火力打擊的兵力為B={b1,b2…bn},其中bk表示第k個火力打擊部隊的編號、兵力種類、打擊參數、執行任務次數、執行任務時長、任務間隔時長等變量集合;敵方目標為D={d1,d2…dm},其中dl表示第l個目標的編號、種類、應毀傷程度、對應彈藥需求量等變量集合;H(dl,bk)、D(dl,bk)、S(dl,bk)、T(dl,bk)分別表示使用第k個火力打擊部隊打擊第l個目標時,對目標造成的毀傷程度,彈藥消耗量,我方兵力預計損耗量,火力打擊總體時長等變量。聯合火力打擊任務規劃問題的硬約束條件如下:

1)保證完成上級賦予的火力打擊任務份額。設任務規劃共包含p個子任務,規定的火力打擊任務份額為G;則約束條件的數學模型表述如下

(1)

2)保證我方各參戰部隊有足夠彈藥應對突發任務。設任務規劃中第k個部隊執行p次任務,每次彈藥消耗量為l,彈藥總量為Lk;則約束條件的數學模型表述如下

(2)

3)保證在規定時限內完成火力打擊任務。設任務規劃共包含p個子任務,發起火力打擊時刻為Ts,規定火力打擊截止時刻為Tz,第k個部隊的火力打擊總時長為Tk;則約束條件的數學模型表述如下:

(3)

max{T1,T2,…,Tk}≤Tz-Ts

(4)

在達成硬約束條件的前提下,設定軟約束條件如下:

1)盡可能在最短時間內對目標實施火力打擊(防止目標逃離)；

2)盡可能節約我方彈藥量,以備不時之需；

3)盡可能減少我各參戰部隊的兵力損耗；

4)盡可能平均分配各部隊的火力打擊任務量；

5)盡可能壓縮總體火力打擊時長；

6)盡可能對同一目標實現多兵器、多彈種聯合火力打擊。

問題的難點:1)各約束條件相互為制約,須通過智能算法建立數學模型找到最佳平衡點;2)目標清單處于動態更新中,隨時會出現新的目標打擊任務,因此聯合火力打擊任務規劃要保證預留部隊和彈藥量應對臨機任務。

2 算法構建

智能優化算法應用于聯合火力打擊任務規劃問題求解,主要由數據錄入、向量空間建立、綜合評估、競爭蛙跳4個部分構成。數據錄入部分將當前態勢下獲取的實時目標情報信息、我方火力打擊部隊的實時信息錄入,結合前期已知的各兵器、彈種對各目標的毀傷能力信息,為后續的智能優化提供數據支撐;向量空間建立部分以打擊部隊，消耗彈藥，打擊目標建立多維空間,將動態兵力、火力、目標分配問題轉化為多維向量空間中尋找最優解向量問題;綜合評估部分以數據錄入為基礎,將固定輸入條件下的聯合火力打擊任務規劃通過數學模型的量化評估指標計算綜合評分;競爭蛙跳部分以向量空間和綜合評估為基礎,通過競爭蛙跳,經過多代迭代,獲取聯合火力打擊任務規劃在向量空間中對應的最佳位置,并將解向量轉化為唯一對應的任務規劃結果輸出。智能優化算法的流程如圖1所示。

圖1 智能優化算法流程圖

2.1 競爭蛙跳模型

標準蛙跳算法以自然界中蛙群為參考對象,設蛙群分散在多個獨立的子群落中,各子群中的最差評分個體可通過有限次數蛙跳向周邊的高分位置轉移,若轉移失敗則引入新個體替代最差評分個體;定期將子群落中的個體打亂重組,防止子群落中的個體陷入局部最優。標準蛙跳算法流程如圖2所示。

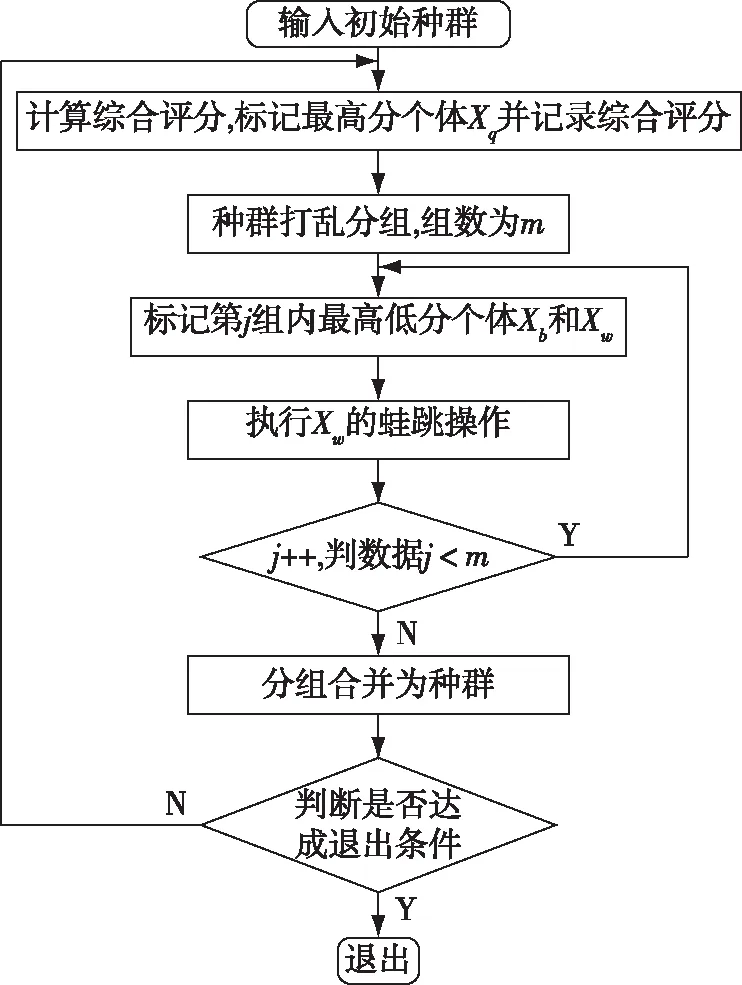
圖2 標準蛙跳算法流程圖

通過對標準蛙跳算法分析可知,其算法核心包含兩部分:一是通過最差評分個體向周邊移動的蛙跳操作探索高分位置;二是定期打亂重組防止算法陷入局部最優。然而算法也存在如下缺陷:一是對偶然產生的局部最高評分個體無法規避,該個體會繁殖眾多類似的后代個體替代低分個體,使種群多樣性受到破壞,導致算法陷入局部最優;二是蛙跳冗余問題,最差評分個體若處于低分區域,但未達到刪除的程度時,算法會頻繁對其實施無意義的重復蛙跳動作,導致系統資源消耗。基于此,本文借鑒遺傳算法中的壽終正寢和優勝劣汰機制,引入壽命和淘汰系數對蛙跳算法進行改造。算法思想是，為了防止局部高分個體的大量繁殖,為所有個體添加壽命系數,設每次打亂重組后為所有個體壽命+1,若有個體壽命達到上限,不論其綜合評分結果如何,均刪除該個體,以模擬自然界的壽終正寢生命歷程;為了防止無意義蛙跳問題,為所有個體添加淘汰系數,設個體的每次蛙跳動作后且評分未提升,則淘汰系數+1,若有個體蛙跳次數達到上限,不論其綜合評分結果如何,均刪除該個體,以模擬自然界的優勝劣汰自然選擇規律。競爭蛙跳算法流程如圖3所示。

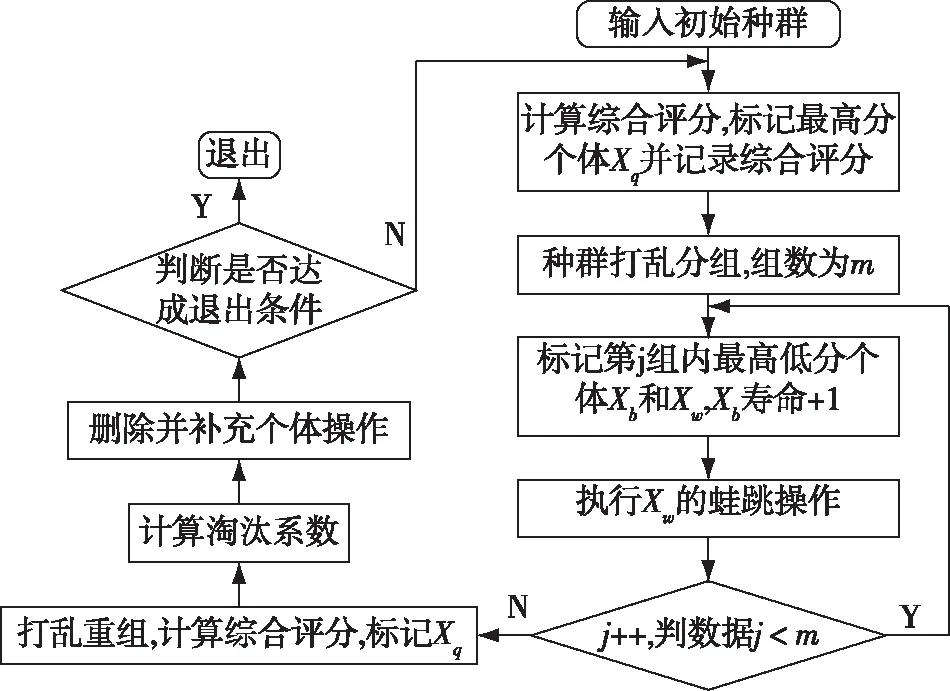
圖3 競爭蛙跳算法流程圖

個體數據結構如表1所示。

表1 個體數據結構

具體算法步驟如下:

Step1:創建初始種群,每個個體對應向量空間中的唯一點位。

Step2:計算種群內所有個體的綜合評分,記錄最高評分個體Xq。

Step3:將種群內所有個體按評分排序,并按序號平均分配到m個子群中,保證各子群內個體總評分相差不大。

Step4:所有個體壽命+1。

Step5:對各子群的最低評分個體Xw實施蛙跳操作,蛙跳后的新位置個體為X′w。

Step6:若X′w的綜合評分高于Xw,則用X′w替代Xw。

Step7:否則重復5-6,若k次蛙跳后的X′w綜合評分低于Xw,則用該子群最高分個體繁殖新個體代替Xw。

Step8:更新所有個體淘汰系數。

Step9:將所有子群打亂重組,記錄最高評分個體Xq。

Step10:重復Step3-8,直至達成退出條件,輸出最高評分個體。

2.2 評估指標模型

本文中針對聯合火力打擊任務規劃的各約束條件,共設計了3類、11項評估指標。具體評估指標如圖4所示。

圖4 聯合火力打擊任務規劃評估指標

設共有m支部隊,第i支部隊打擊半徑為oi,可執行打擊任務次數為ci,任務執行時長di,任務間隔時長ei,部隊所在地坐標為(xmi,ymi);目標打擊表中共有n個目標,第j個目標的標準毀傷程度為hj,目標所在地坐標為(xnj,ynj);毀傷能力表中第i支部隊對第j個目標火力打擊,毀傷40%對應出動次數為g40ij,毀傷60%對應出動次數為g60ij;火力打擊任務規劃中共有子任務r個,第k個子任務的執行任務次數為lk,打擊開始時刻為pk,打擊結束時刻為qk;u為部隊每次執行任務后的兵力損耗百分比。首先要對任務規劃進行可行性判斷。

1)剔除超過部隊射程的子任務,計算公式為

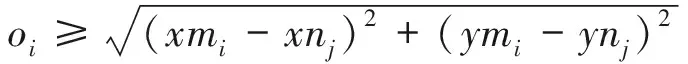
(5)

2)剔除超出最大出動能力的子任務,計算公式為

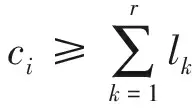
(6)

然后計算各評估指標。

1)單目標打擊時長(Aj)。用以表示對第j個目標實施聯合火力打擊的總用時,計算公式為:

Aj=max{qj}-min{pj}

(7)

2)單部隊打擊次數(Bi)。用以表示第i個部隊已實施火力打擊的次數,計算公式

(8)

3)整體打擊時長(C)。用以表示該任務規劃的聯合火力打擊總用時,計算公式為

C=max{qk}-min{pk}

(9)

4)單目標冗余彈藥比例(Ej)。用以表示對第j個目標實施聯合火力打擊的彈藥用量,超過規定毀傷彈藥用量的比例。設投入彈藥比例為Dj,s表示目標等級,d表示出動次數;計算公式為

(10)

Ej=max{0,Dj-100}

(11)

5)單目標完成任務比例(Fj)。用以表示任務規劃中對第j個目標實施聯合火力打擊的任務完成度,計算公式

Fj=min{100,Dj}

(12)

6)體系破擊能力(Gr)。用以表示完成第r個子任務時,對敵體系作戰能力的破壞程度,計算公式為

(13)

7)防空削弱能力(Hr)。用以表示完成第r個子任務時,對敵防空能力的破壞程度,計算公式為

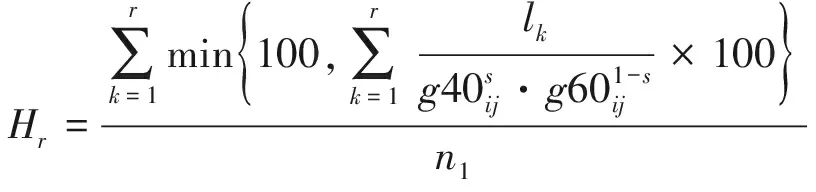
(14)

8)地面打擊削弱能力(Ir)。用以表示完成第r個子任務時,對敵地面打擊能力的破壞程度,計算公式為

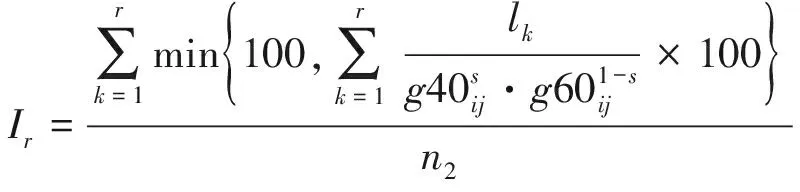
(15)

9)彈藥剩余比例(Ji)。用以表示第i個部隊執行完火力打擊任務后的彈藥剩余比例,計算公式為

(16)

10)兵力剩余比例(Ki)。用以表示第i個部隊執行完火力打擊任務后,按照敵方的體系破擊能力、防空削弱能力、地面打擊削弱能力情況,預測剩余的兵力占原有兵力的比例,計算公式為

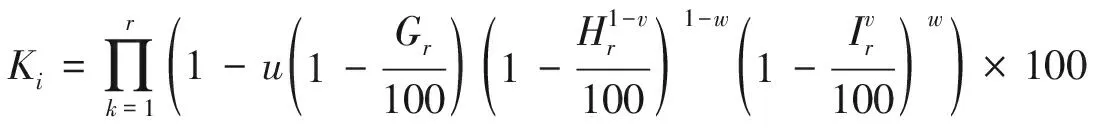
(17)

11)聯合打擊次數(L)。用以表示對各目標實施聯合火力打擊過程中,實現了多種兵器、多種彈藥在同一時刻對同一目標實施復合火力打擊的次數,計算公式為

(18)

(19)

2.3 綜合評分模型

本文使用熵權法[16]將單目標指標和單部隊指標進行融合處理,生成唯一對應的評估指標,而后使用理想點法[17]將11項評估指標綜合計算評分。以單目標指標的融合計算過程為例,設共有m個火力打擊目標,有n個任務規劃參與評估,建立初始矩陣X;熵權法的計算流程如下:

Step1:歸一化處理。生成歸一化矩陣P,計算公式為

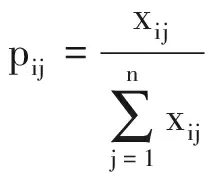
(20)

Step2:熵值計算。生成m個目標的對應熵值ej,計算公式為

(21)

Step3:熵權重計算。生成第m個目標的對應熵權重tj,計算公式為

(22)

Step4:融合評估指標計算。生成n個任務規劃的融合評估指標值zi,計算公式為

(23)

當獲取n個任務規劃的11項評估指標后,使用理想點法的計算流程如下。

Step1:計算正負理想點A+和A-,計算公式為

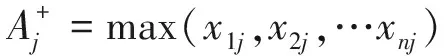
(24)

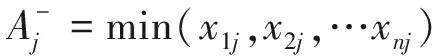
(25)

Step2:計算第i個任務規劃與正負理想點之間的距離di+和di-,計算公式為

(26)

(27)

Step3:計算第i個任務規劃的綜合評分Mi,計算公式為

(28)

3 仿真分析

為了驗證競爭蛙跳算法在聯合火力打擊任務規劃中的優化效果,本文采用文獻[5]提供的標準蛙跳算法作為對比算法。仿真實驗計算機配置為Intel酷睿雙核處理器T7300 2.0 GHz，3G內存，Window 7 32位操作系統，vc6.0編程平臺。

3.1 參數有效性分析

為了驗證最優搭配組合的參數設置,設計實驗如下:選取變異概率、種群規模、蛙跳步長、蛙跳嘗試次數、壽命上限、淘汰系數上限、退出條件代數為待調節參數,每次調整其中一個參數的取值范圍,并通過競爭蛙跳算法的多代迭代最優評分為參考條件,將參數調整為最佳位置,如此反復,直至所有參數均達成最優值,輸出最優評分個體。所有參數的最優值如表2所示。

3.2 效果對比分析

為了檢驗算法的優化效果,以標準蛙跳算法和標準遺傳算法作為對比實驗,計算經過500代迭代進化的最優個體綜合評分結果。算法最高評分對比變化情況和各代最高評分對比變化情況如圖5和圖6所示。

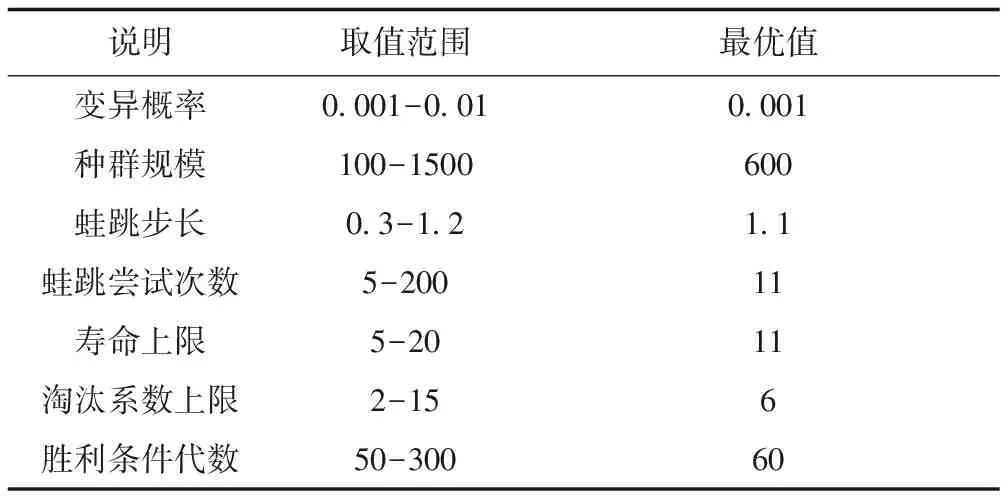
表2 參數優化統計

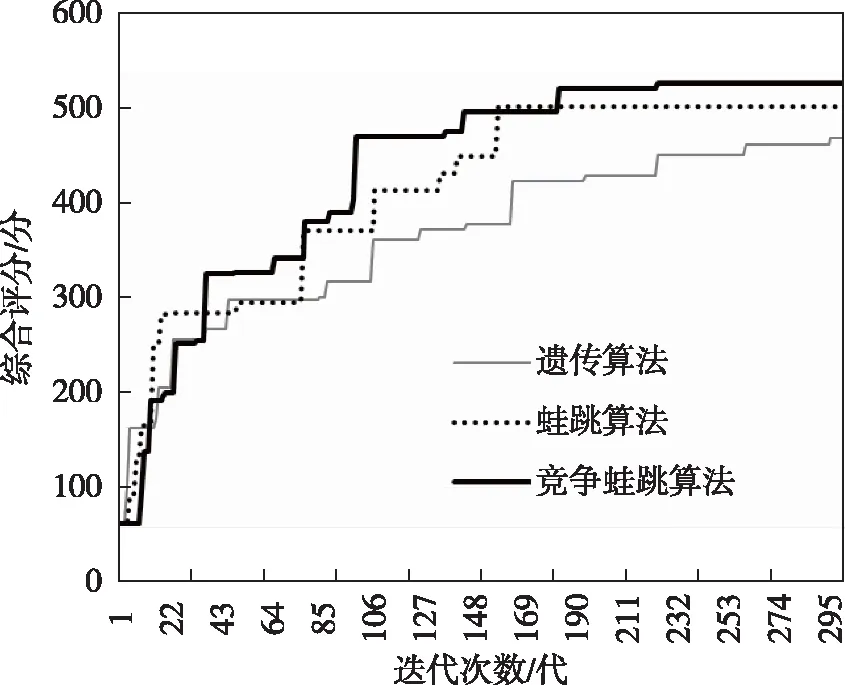
圖5 最優個體綜合評分對比

圖6 各代最高評分對比

實驗結果表明,競爭蛙跳算法相比于標準蛙跳算法和標準遺傳算法,收斂速度更快,能夠在較少代數內達成全局最優。圖6中,標準蛙跳算法的各代最優個體評分抖動不大,表明高分的超級個體影響了算法的尋優能力,限制了種群的多樣化發展方向;相比而言,競爭蛙跳算法的各代最優個體評分抖動明顯,表明種群正在向多樣化發展,試圖突破當前位置局限,尋找全局最優解。

3.3 規劃結果分析

為了檢查算法在聯合火力打擊任務規劃具體問題中的應用效果,將三種算法得到的最優個體進行對比分析。三種算法的時間消耗對比情況如圖7所示,收斂代數對比情況如圖8所示。

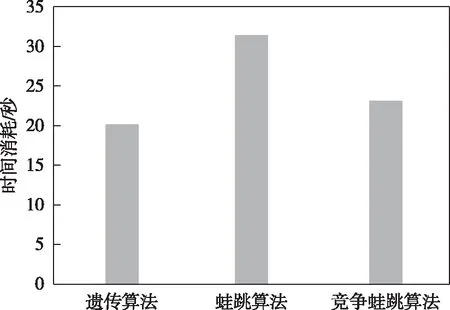
圖7 算法時間消耗對比

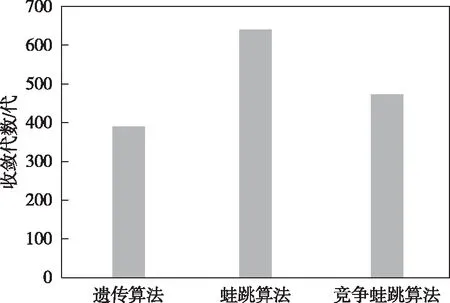
圖8 算法收斂代數對比

實驗結果表明,競爭蛙跳算法由于引入了淘汰系數,蛙跳更具方向性,同時避免了無意義的重復蛙跳動作,因此收斂代數更短,時間消耗更少。對標準蛙跳算法和競爭蛙跳算法得到的任務規劃11項評估指標進行對比分析,兩種算法的評估指標對比情況如圖9所示。

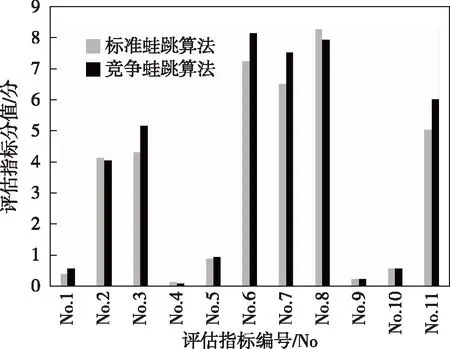
圖9 算法評估指標分值對比

實驗結果表明,除了單部隊打擊次數(No.4)和體系破擊能力(No.8)評估指標外,競爭蛙跳算法的各項評估指標均優于標準蛙跳算法,由此可知,標準蛙跳算法獲取的最優個體并不是全局最優個體,競爭蛙跳算法相比較而言具備更優異的全局尋優能力。

競爭蛙跳算法對應的聯合火力打擊任務規劃示例如表3所示。

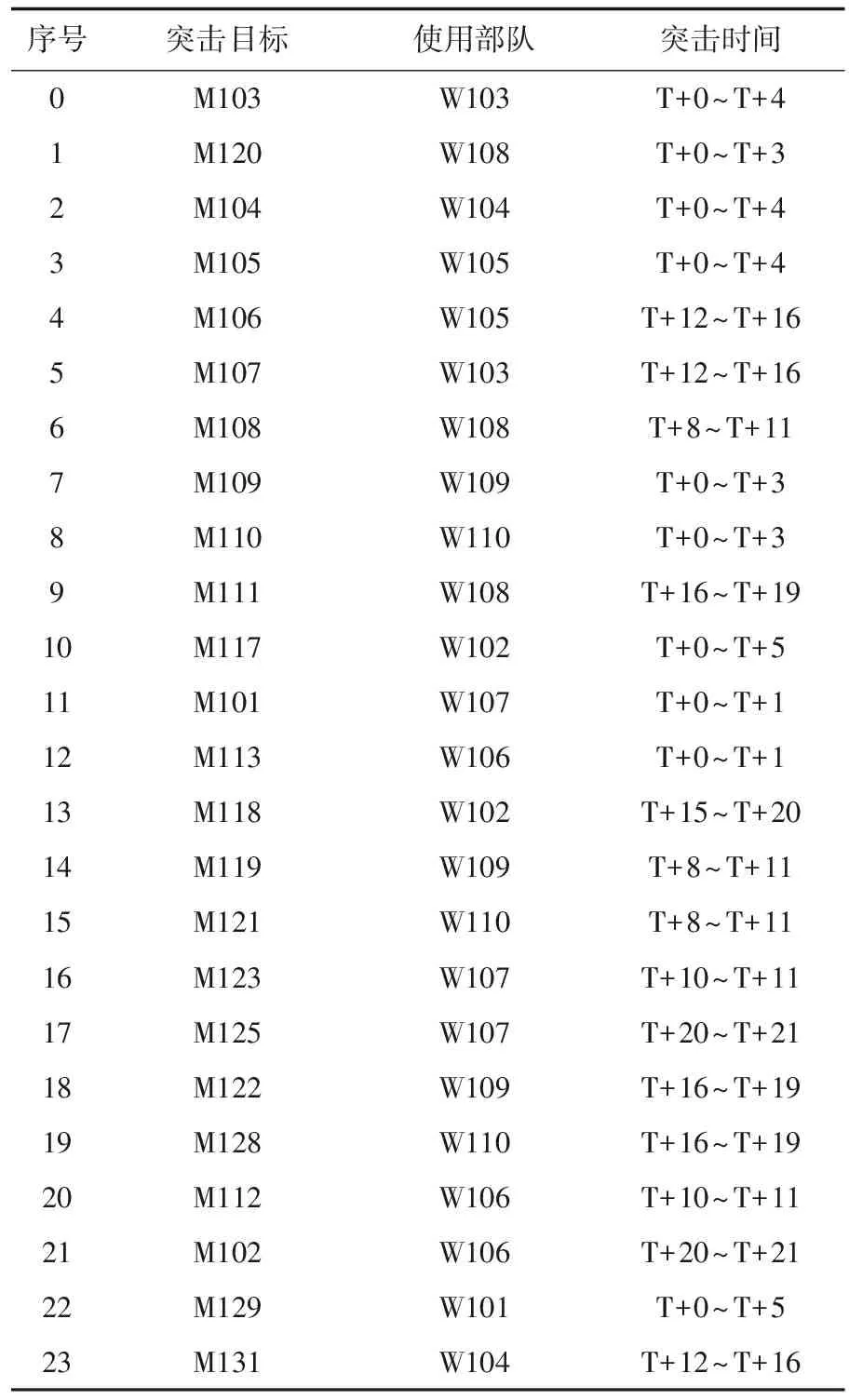
表3 聯合火力打擊任務規劃輸出示例

4 結束語

本文在前人對智能優化算法研究的基礎上,創造性地將遺傳算法中的壽終正寢和優勝劣汰機制引入到蛙跳算法中,設計了綜合效果更優異的競爭蛙跳算法,并以此為基礎實施聯合火力打擊任務規劃,通過競爭蛙跳算法的多代迭代獲取最優的規劃計劃,使任務規劃綜合評分達成全局最優。創新點有，一是梳理了聯合火力打擊任務規劃的硬性和軟性約束條件,并提出了量化評分算法,實現了對聯合火力打擊任務規劃的量化評估;二是設計了新的智能優化算法——競爭蛙跳算法,經仿真實驗驗證,優化分值和收斂效率均高于標準算法;三是將智能優化算法引入聯合火力打擊任務規劃問題中,實現了基于計算機的自動優化評估。仿真實驗結果表明,該方法可引入到聯合火力打擊任務規劃問題優化中,能夠動態生成最優的任務規劃,并以此為基礎擬制火力打擊方案和計劃,并提出量化的輔助決策建議,為聯合作戰指揮員定下火力打擊決心提供參考標準。