分數階偏微分方程求解與優化模型對高溫防護服設計的計量分析

王 寶， 朱家明

(安徽財經大學a.金融學院；b.統計與應用數學學院， 安徽 蚌埠 233000)

引 言

高溫作業是伴隨著高溫、高輻射以及高氣濕等異常作業條件下致使濕球黑球溫度指數(WBGT指數)超過一定標準的作業，通常分為高溫以及強輻射作業、高溫高濕作業和夏天露天作業三種，通常發生在冶金工業作業、耐火工業作業以及潛水艙作業等情況中，而實際研究結果表明高溫作業往往會對人體造成極大的不同程度的影響。在生理功能方面，高溫作業會導致肌體損失水分以及人體必需的微量元素，引起消化系統出現消化不良以及腸胃病發病率的提高，由于失水過多也會引發腎功能不全以及蛋白尿等連鎖反應；同時也會導致由于產熱及受熱超過散熱引發的熱射病，大量脫水導致水與電解質比例失調引發的熱痙攣和由于失水造成循環血量減少引發的熱衰竭等[1]。高溫作業防護服是在高溫環境下能夠防止人體產生不適的防護衣服，具有阻燃性、聚液性、服裝完整性、穿著舒適性等性能[2]。目前開發研制的新型熱防護材料有芳砜綸纖維、NomexⅢA等，另外相變材料的應用也成為熱防護服研究的熱點。熱防護服織物的加工方法目前主要是純紡法、混紡法、涂層加工法和多層織物復合法[2]等，優良的熱防護服既要對外界熱量具有良好的阻隔作用，又要達到一定的熱濕傳遞能力，以利于人體熱量釋放和汗液蒸發[1]。但是，目前在熱防護服和研究開發中，增強熱防護性能與減少人體新陳代謝熱負荷總是相互矛盾的，解決這一問題既是對科研工作者的挑戰，又是一個機遇。因此高溫熱防護服設計對高效完成高溫作業工作和相關科技研究具有較大意義。

而在近幾年已有的研究體系下，國內部分專家學者已對高溫傳導，熱量傳遞，高溫熱防護服設計等做了相應研究，探索出了相關結果。但也存在部分不足和局限性。例如，盧琳珍[3]在《多層高溫作業防護服裝的熱傳遞模型及參數最優決定》中基于變系數拋物型方程建立并驗證多層熱防護熱傳遞模型。該文對改進的變系數拋物型方程進行收斂性分析并對各層接觸面給出合理的處理方式。不足之處是該文并未考慮濕傳遞對防熱服的影響程度；蔣曉穎[4]在《兩類空間分數階擴散方程反問題研究及其在高溫作業防護服設計中的應用》中基于空間分數階熱傳遞模型并綜合皮膚層熱傳遞模型對高溫環境下防熱服的傳遞問題進行探究。不足之處是考慮的影響因素并不全面，并未考慮到防熱服不同層所處的環境不同，是否應采用不同的熱傳遞模型加以描述;余躍[5]在《紡織材料熱濕傳遞數學建模及其設計反問題》對空間分數階熱傳遞模型進行了理論分析得出該模型適合特定的溫度環境。同時該文討論了不同溫度環境下的熱傳遞過程。不足之處是在分數階方程只能達到一階的精度，并未解決高階問題。本文的創新之處在于將之前已研究的局部條件狀況進行綜合運用，設置環境溫度為65 ℃時，工作60分鐘且假人皮膚外側溫度不超過47 ℃，超過44 ℃的時間不超過5分鐘；以及環境溫度為80 ℃時，工作30分鐘假人皮膚外側溫度不超過47 ℃，且超過44 ℃的時間不超過5分鐘兩種模擬實驗條件，從不同問題角度使用不同算法進行探討，在對已有算法基礎上針對條件進行簡明創新，使算法的使用更加直接簡練。

本文通過建立數學模型，研究在高溫環境下實驗模擬假人皮膚表面外側溫度不斷變化時，高溫熱防護服中材料層溫度發生的變化；在已知實際高溫作業條件限制下針對高溫熱防護服材料層厚度設計并優化，為相關熱防護服設計和研發提供進一步模型支持。

1 數據來源與假設

本文數據主要來源于2018年全國大學生數學建模競賽主辦方提供。為了更方便對參數進行求解和科學高效的解決問題，特提出以下假設：①高溫作業防護服中同一織物層不同方向上具有相同性以及同一織物層中不同區域吸收熱量是相同的；②由于其他無關因素如水分和濕度等因素變化導致的高溫作業防護服體積變化忽略不計，并將有效曲折系數設為常數；③“環境-服裝-皮膚”系統中熱傳遞過程僅考慮熱傳導與熱輻射的傳熱過程，不考慮其它熱傳遞過程；④高溫作業防護服中各織物層在防熱過程中未發生熔融與分解；⑤假設高溫作業防護服不同織物層的輻射系數固定不變。

2 基于熱傳導分數階偏微分方程求解對材料層溫度分布研究

2.1 研究思路

專用服裝通常由三層織物材料構成，記為I、II、III層，其中I層與外界環境接觸，III層與皮膚之間還存在空隙，記為IV層空隙層。以環境與高溫作業防護服接觸點為原點，各點與環境的距離為x軸，環境與高溫作業防護服接觸面為y軸，建立“環境-防護服-皮膚”系統[6]，如圖1所示。

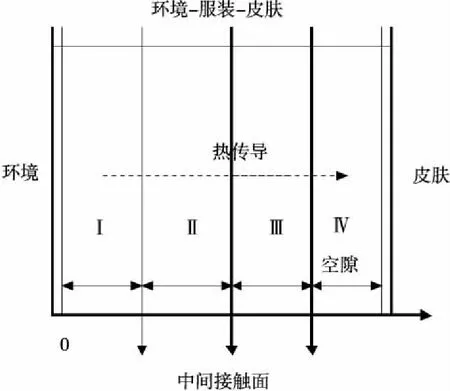
圖1 “環境-防護服-皮膚”系統

根據已知不同層次的密度、比熱、熱傳導率以及厚度四個指標，可以反映三個層面織物的熱傳導效率。而要利用已知參數信息對環境溫度為75 ℃、Ⅱ層厚度為6 mm、Ⅳ層厚度為5 mm、工作時間為90分鐘的條件下求解Ⅲ層材料層的溫度分布，可通過對不同織物熱傳導效率，環境溫度、不同織物厚度以及工作時間等參數研究，將三個織物層次(Ⅰ，Ⅱ，Ⅲ)看成一個熱傳導方式相同但參數不同的系統，考慮織物層熱傳遞過程，同時分析空隙層(Ⅳ)的熱傳遞過程，建立分數階偏微分方程，對不同時刻的假人身體溫度進行刻畫。研究思路如2所示。

圖2 研究思路流程

2.2 研究方法

在高溫環境中，熱量主要經過熱傳導和熱輻射作用穿過高溫防護服與空氣間隙，作用于人體皮膚表層使人體溫度逐漸升高，根據物理學中熱學相關理論知識對熱傳導和熱輻射做簡單相關闡述。

在溫度場中某一時刻τ下同一等溫線上某點y=f(x,y,z,r)，且在具有連續溫度場的情況下，用溫度梯度gradt描述過任意一點的最大溫度變化率，即

(1)

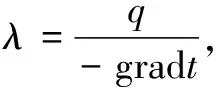
(2)

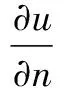
k(uxx+uyy+uzz)

(3)

結合能量守恒定律與比熱，密度關系，可將Fourier定理改寫成[8]：

(4)

另外值得注意的是，在初始階段，假人皮膚表層溫度對防護服第四層同樣起著熱傳導作用，即人體本身溫度作為內部熱源。同樣在dt時間內，在物體內部任何一點所產生的熱量為Q(x,y,z,t)，可得出含熱源的熱傳導方程：

(5)

如果時間足夠長，溫度不再變化，此時u′=0，得到穩定條件下有熱源Laplace方程：

▽2u=f

(6)

在對熱傳導偏微分求解和Fourier定理理解基礎上，對于高溫高溫作業防護服的多層熱傳遞模型，考慮到高溫作業防護服在與環境接觸的接觸面在高溫下存在反常擴散現象[9]，基于此物理現象，在熱傳導求偏微分的基礎上考慮使用分數階偏微分方程的擴散模型[10]，具體表示如下：

①高溫作業防護服中的分數階偏微分方程模型

首先，先考慮高溫作業防護服中的熱傳遞，根據高溫作業防護服的溫度T(α,t)和高溫作業防護服左邊界與右邊界的熱輻射建立方程組：

(7)

環境的初值條件：

T(α,0)=T1(α),α∈A

高溫作業防護服左邊界條件：

(8)

其中，從熱源到高溫作業防護服過程中產生的熱通量為：

(ρ1+ρ2)|α=0=m(T0-T1)

(9)

高溫作業防護服中第Ⅰ層與第Ⅱ層的接觸面：

(10)

高溫作業防護服中第Ⅱ層與第Ⅲ層的接觸面：

(11)

高溫作業防護服的右邊界條件：

(12)

②高溫作業防護服與皮膚層之間空隙(即IV層)分數階偏微分方程模型空隙層的初始條件為：

T(α,0)=T1(α)

空隙層的分數階偏微分方程模型為：

(13)

2.3 問題求解

針對 “環境-服裝-皮膚”系統建立的分數階微分方程進行數值離散：

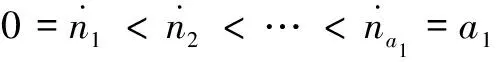
前三層織物層的離散為：

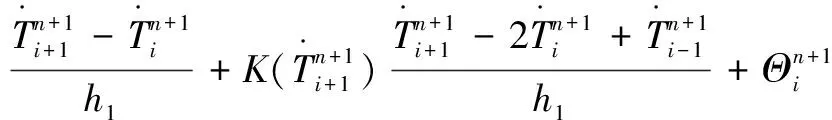
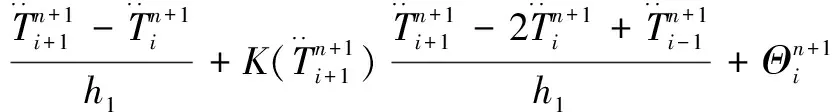
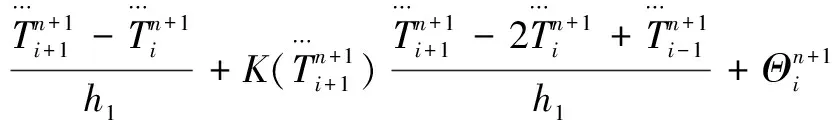
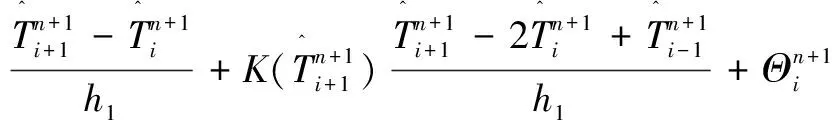
其中，i=1,2,…,a1-1；n=0,1,…,N-1。

假設

則：

其中，i=1,2,…,a1-1；n=0,1,…,N-1。

III層織物層的左邊界離散：

(14)

假設

則III層織物層的右邊界離散：

(15)

空隙層的左邊界條件離散：

(16)

空隙層的右邊界條件離散：

(17)

2.4 結果輸出

熱防護服材料主要參數見表1，根據已知參數對已構建偏微分方程進行求解。

表1 熱防護服材料主要參數

結合Matlab等數學計量軟件計算，初步擬合出方程為：

y=9.093e-9x2-3.031e-5x3+0.03252x+36.72

畫出溫度分布方程圖像，如圖3所示。

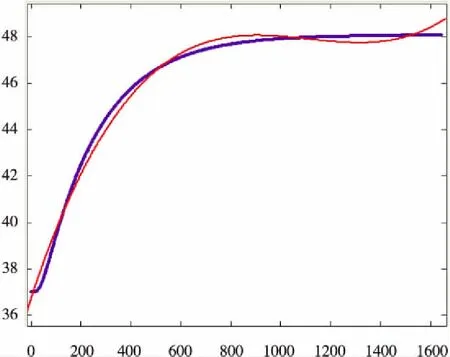
圖3 擬合曲線與已知實驗值對比圖

由此擬合出在環境溫度為75 ℃、Ⅱ層厚度為6 mm、Ⅳ層厚度為5 mm、工作時間為90分鐘的條件下實際作業限制條件下熱量傳導擬合圖，如圖4所示。

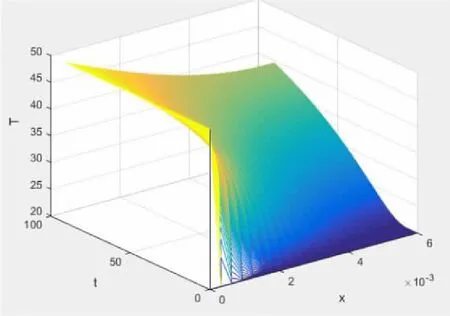
圖4 熱量傳導擬合圖

3 基于非線性優化算法對單層材料層最優厚度研究

3.1 粒子集群算法對最優厚度設計的使用

下面我們在環境溫度為65 ℃時，確保工作60分鐘假人皮膚外側溫度不超過47 ℃，且超過44 ℃的時間不超過5分鐘條件下，確定II層最優厚度。

3.1.1 研究方法

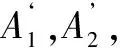
對于內層有如下一維穩態熱傳遞模型：

(18)

對織物外層有：

(19)

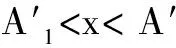
T(x)|x=A′=TR

(19)

在上文建立的熱傳導模型基礎上，可得出Ⅱ層熱傳導過程，結果如下：

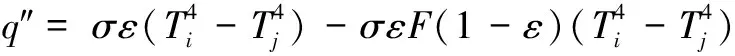
(20)

可以確定Ⅱ層的厚度為A2-A1，其中：

α1=0.06 mm,α2=(A1-0.6) mm,

α3=3.6 mm,α4=5.5 mm

第II層的初始條件為：

T(α,0)=(α2,0)=T(A1-0.6,0)

第II層的左邊界條件為：

第II層的右邊界條件為：

(21)

由題意可得到約束條件為：

T(x,t=3600)≤47 ℃

T(x,t≤3600)≤44 ℃

聯立上述方程，可利用Lingo運算得出：α2≥9.2。

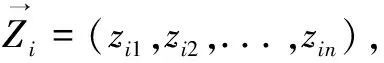
第一步：選擇閾值ε和最大迭代次數Nmax；每個粒子的初始位置和初始速度分別為：

3.1.2 結論分析

由輸出結果可以看出，在環境溫度為65 ℃，IV層的厚度確定且等于5.5 mm情況下，在t≤3600s，滿足約束條件T(x,t=3600)≤47 ℃，T(x,t≤3600)≤44 ℃，從非穩態到穩態狀態和制作成本等角度考慮，Ⅱ層最優厚度可取9.2 mm。

3.2 簡單遺傳算法對單層材料層最優厚度研究分析

在環境溫度為80 ℃時，確保工作30分鐘假人皮膚外側溫度不超過47 ℃，且超過44 ℃的時間不超過5分鐘條件下，確定II層和IV層的最優厚度。

3.2.1 研究思路

對于當環境溫度為80 ℃時，確定II層和IV層的最優厚度，確保工作30分鐘時，假人皮膚外側溫度不超過47 ℃，且超過44 ℃的時間不超過5分鐘的問題。首先將皮膚外側溫度轉化為皮膚熱損傷程度的問題，建立反方向理論模型[11]。在熱損傷程度與防護服厚度的限制條件下，建立目標函數及離散形式，最后對離散方程進行正則化處理，通過遺傳算法求解得到最優厚度。可簡化思路如圖5所示。

圖5 遺傳算法思路分析圖

3.2.2 研究過程

為了改善高溫作業防護服的厚度，采用Henriques積分來做標準[12]。以此為準則，當基底層(這里表示為人體外側皮膚中間接觸面)溫度達到44 ℃時，人體皮膚就會發生熱損傷。長時間在高溫條件下工作，防護服很難滿足保持舒適的要求；另外，高溫工作人員的人身安全是最主要考慮的事情。因此，提出的反問題目標為皮膚熱損傷程度最小或者避免熱損傷。為了預測皮膚的損傷程度，將接觸面溫度代入下面積分：

(22)

其中，積分的時間區間為人體外側皮膚溫度超過44 ℃之后的時間。T取基底層的溫度，當基底層滿足Ω|x=A1+A3≤1，不會發生熱損傷。P和ΔE的值見表2。

表2 P和ΔE的數值分布[14]

以人體外側皮膚接觸面作為目標點，滿足Ω≤1即認為沒有發生熱損傷，將發生熱損傷的臨界Ω記做Ω·。對于正問題而言，如果知道相應的參數，就可以算出熱損傷的程度及時間。那么在反問題中，在給定的工作時間內，保證安全的同時能夠使得皮膚損傷程度最小的最優參數，即求L,k，使得：

(23)

當不考慮Ω>Ω*=1的部分，則Ω與Ω=1所圍成的面積越大表示著熱損傷程度越低，也就是人體外側溫度超過44℃的時間越短。因此將防護服厚度優化的問題轉化為下列目標函數：

(24)

這樣原來優化函數求最小值就轉化成求該方程組的最大值點。

已知在基層處(x=A1+A3)任意時刻的溫度T(t)=T(A1+A3,t)， Ω(t)=Ω(A1+A3,t)。這里，選取最優II層和IV層的厚度A2和A4，將Ω(t)改寫為Ω(t,A)，其中A=(A2，A4)。由前面分析可知，當Ω<1，人體外側皮膚沒有達到熱損傷程度，認為是安全的。我們只在安全前提下討論反問題。工作時間取30分鐘，燒傷程度取Ω*=1，故上述目標函數可改寫為：

(25)

改寫為離散形式為：

(26)

最優解即為求該方程的最大值點。

3.2.3 問題求解

現實生活中防護服的制造還受到厚度上的限制，例如A2+A4≤Amax=31.4。首先對離散式(10)進行正則化處理，再使用遺傳算法進行求解，得到下列目標函數：

(27)

其中，參數β稱為正則化參數，該目標函數的解即是滿足安全指標與厚度限制的最優解。Qβ(A2,A4)即是該方程的極小值點(A2*,A4*)，稱為反問題的正則化解。具體方法表述如下：

①給定工作時間t*=1800 s

②劃分情況：Amin=A′

③求解DP，獲得Qβ(A2,A4)

對β的處理將對結果產生直接的影響。這里我們采用先驗誤差，取β=10-6，另外賦值遺傳算法的其他參數：個體數目為40，迭代數目為100，變量個數為2，每個變量的25位數字表達為25，代溝數為0.9。這里我們將運行50次的最大值作為最優解，得出A=(10.6,4.2),且Q(A)=0.9906。即II層最優厚度為10.6 mm，IV層的最優厚度為4.2 mm。結合實際研發，可從工作時間和具體工作環境角度進行合理化設計。

4 結束語

本文結合之前高溫防護服相關設計研究的基礎上，建立了完整的“環境-服裝-皮膚”系統熱傳遞模型。考慮到高溫作業防護服的左邊界處于高溫狀態時會發生反常擴散現象，基于此現象提出分數階微分方程的熱傳遞模型并求解得出單層在特定條件下溫度分布。在對高溫作業防護服最優厚度確定時，以安全性作為指標，結合其他織物層的熱傳導過程，建立了反問題模型，以最優參數的確定和粒子集群算法來求解最優解。遺傳算法作為全局優化算法，不需要深入研究問題的內在特性。對于任意形式的約束與目標函數，無論是連續還是離散，線性還是非線性都可處理。本文總體研究思路、模型建立與求解過程簡明有效，具有較強理論和實證性，可為相關高溫熱防護服設計及其衍生產業發展提供理論依據與實驗解釋，提供相關參考依據。