函數點缺陷對光子晶體帶隙結構的調制

張曉茹，張瀝元，張 鑫，杜佳樂，蘇靖淇，韓雨欣，吳向堯，劉曉靜

（吉林師范大學物理學院，吉林四平136000）

1987年Yablonovitch和John分別獨立提出光子晶體的概念[1-2]。光子晶體由兩種或兩種以上不同介電常數的材料構成，其重要特征為光子帶隙、缺陷態、光局域化等[3-7]。利用這些特點，可以用來制造一些全新的高性能設備，如高效的半導體激光器、發光二極管、光學濾波器、波導、光學衰減器以及光學放大器[8-11]等。光子晶體具有周期性，因此完整光子晶體帶隙結構中會出現一條很寬的禁帶，當引入缺陷來破壞光子晶體的周期結構時，原來處在禁帶中的光頻率與束縛態的頻率一致時，就會發生諧振，使原本被禁止的光子在禁帶中傳播，并在缺陷處形成一個量子化束縛態，形成缺陷模。近年來，廣大學者研究了介質柱介電常數為常數的點缺陷對光子晶體帶隙結構的影響，并為光學器件的設計提供了很好的思路[12-14]。

本課題組進一步研究當介質柱的介電常數為函數形式時，函數系數k的改變對光子晶體帶隙結構的調節作用。文獻[15-18]提出了二維函數光子晶體的概念，并研究了二維函數光子晶體中TE和TM波的帶隙結構及Dirac點分布。二維函數光子晶體不同于二維常規光子晶體，其介質柱折射率是隨空間位置分布的函數，可通過對介質柱施加外電場、光場來改變其折射率，即通過電光效應和Kerr效應使介質柱折射率成為空間位置的分布函數。在一階電光效應中，點缺陷的介質柱介電常數函數形式為εr=n20+2αE,可以通過法拉第電磁感應定律得到外加電場為沿介質柱半徑r線性分布的函數E=E0r+d，則介電常數可寫為εr=2αE0r+n20+2αd=kr+b，其中k=2αE0，b=n20+2αd，E0為電場幅值，α為電光效應系數，d為參數，b為可調參數（無量綱），k為函數系數（單位為m-1），此時介電常數為沿半徑r線性分布的函數。當函數系數k=0時，介質柱的介電常數為常數；當k≠0時，介質柱的介電常數為沿半徑r線性分布的函數。可見，通過電光效應可使介質柱介電常數成為空間坐標函數，即點缺陷介質柱的介電常數為函數形是可以實現的。

本文在研究二維光子晶體中加入兩個函數點缺陷時，點缺陷介質柱介電常數函數形式為εr(r)=k r+b，其中可調參數k的變化可通過電光效應實現，通過調節函數點缺陷的介質柱介電常數參數就可實現光子晶體帶隙結構的調制。

1 二維函數光子晶體介電常數的傅里葉變換

文獻[15-16]給出了二維函數光子晶體介電常數的傅里葉變換，介質柱的介電常數為

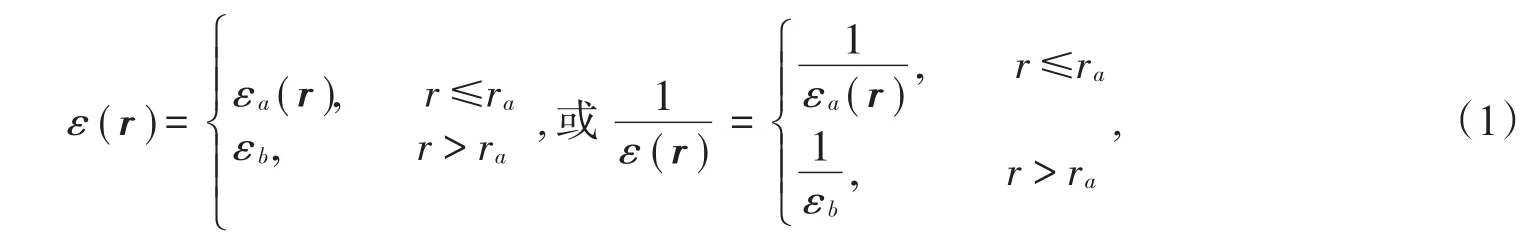
（1）式可以寫為

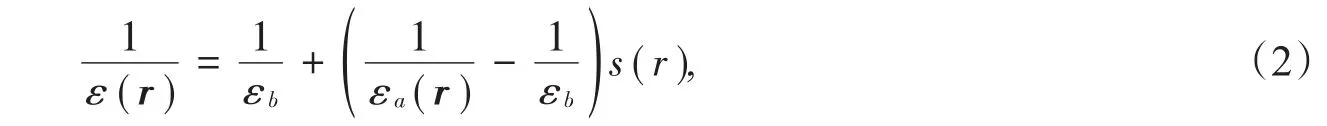
其中

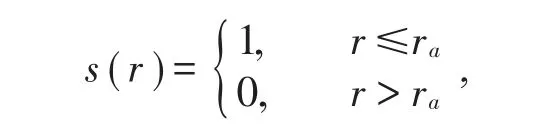
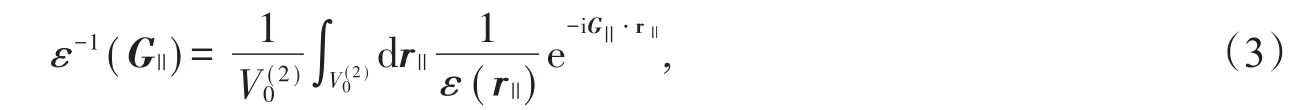
其中G||=m1b1+m2b2，r||=xi+yj，V(2)0為二維空間單原胞體積。

將（2）式代入（3）式得

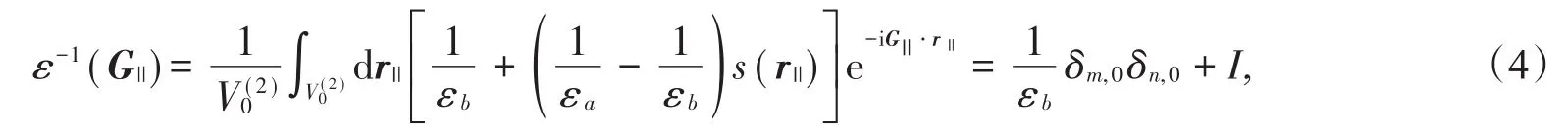
其中

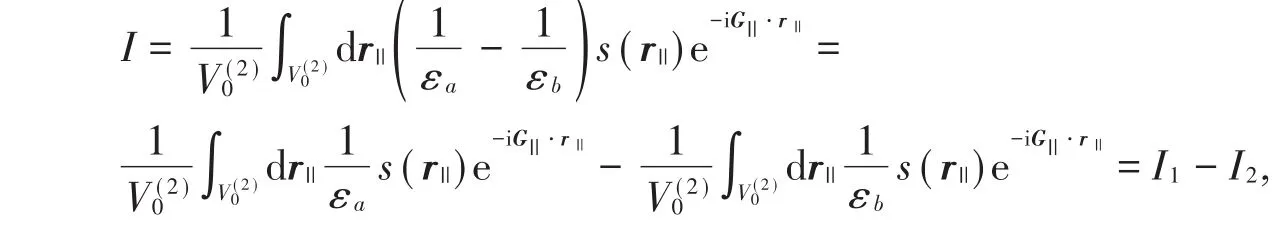
有

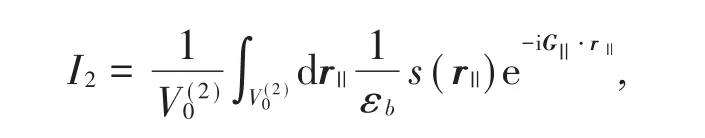
有|r|||=r||=r，|G|||=G||，dr||=ds=rdrdθ，θ為r||和G||的夾角。通過計算可知

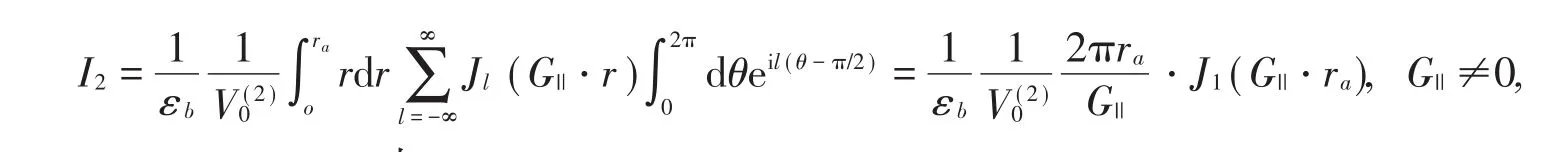
當G||→0 (m→0,n→0)時，

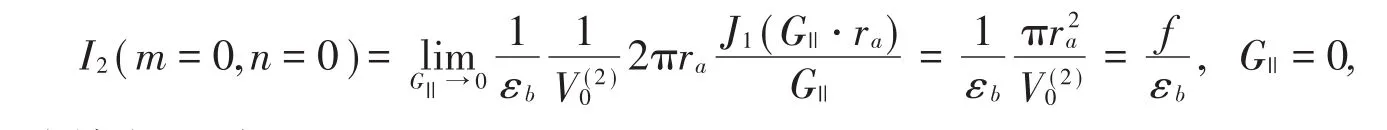
其中，f=πr2a/V(2)0為填充比，有

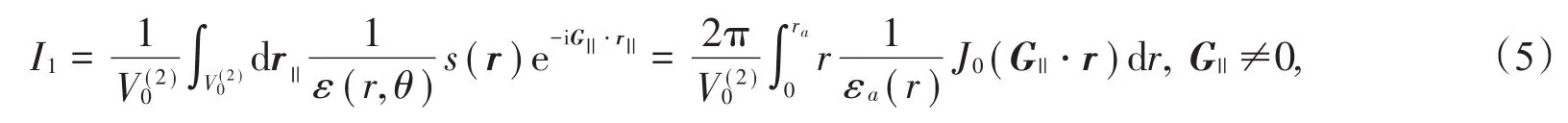
在方程（5）中，考慮εa(r,θ)= εa(r)，當G||=0時，則有

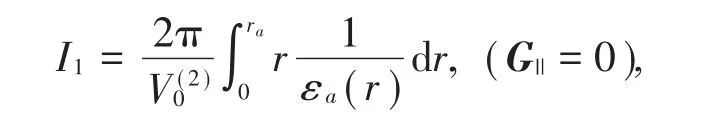
將I1，I2,和I代入（4）式可得

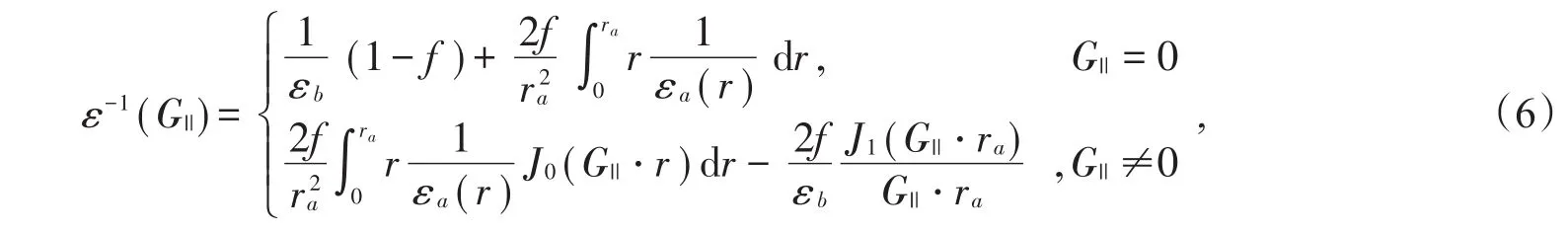
其中εa(r)= εa，εa為常數，則（6）式可以寫為

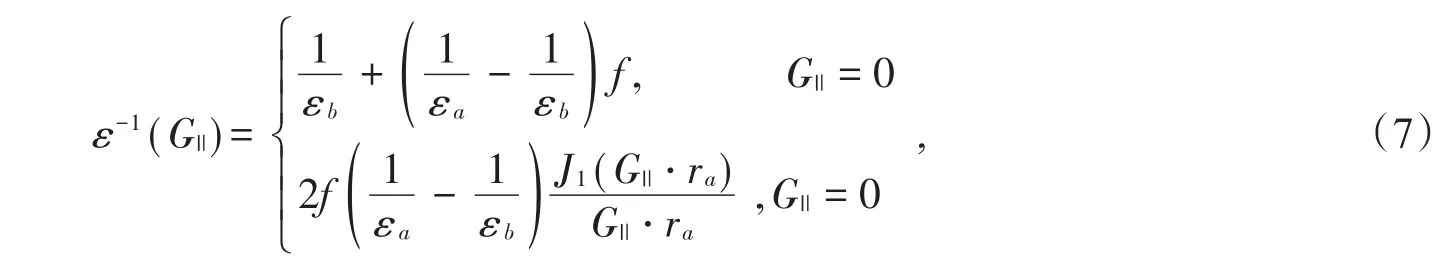
（7）式是二維常規光子晶體介電常數的傅里葉變換，可見二維常規光子晶體是二維函數光子晶體的一種特殊情況。通過平面波展開法，給出了TE波的特征方程為

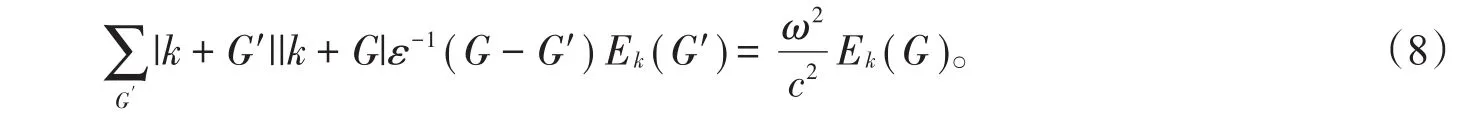
將（7）式代入（8）式可以得到二維函數光子晶體的帶隙結構。

2 數值分析

根據上述理論計算和COMSOL仿真軟件模擬二維光子晶體帶隙結構和本征場分布。本文中，我們研究介質柱按正方形結構周期性排列在空氣中的二維光子晶體，當加兩個函數點缺陷時，通過改變點缺陷介質柱介電常數的參數k的數值，研究其對帶隙結構的影響，并給出含缺陷的本征場在Ez方向的本征場分布。圖1為含缺陷的正方結構二維光子晶體結構圖，白色圓圈為介質柱，其介質柱介電常數為常數，藍色兩個圓圈為兩個點缺陷，其介質柱介電常數為函數，其函數形式為εr=kr+b（0≤ra≤0.5a），ra為介質柱的半徑，晶格常數a=10-7m。在光子晶體中選取7×7超原胞結構，如圖中虛線矩形框內所示。

圖1 含缺陷的正方結構二維光子晶體結構圖

首先，通過COMSOL仿真軟件模擬計算二維完整結構光子晶體帶隙結構，其中，介質柱的εr=9，ra=0.3a，帶隙結構如圖2（a）所示。由圖2（a）可看出，在頻率0.26～0.34內出現一條很寬的禁帶。圖2（b）中陰影部分是由3個高對稱點Γ、X、M所定義的簡約布里淵區，其坐標分別為Γ=2π/a[0,0]，X=2π/a[0.5,0]，Γ =2π/a[0.5,0.5]。

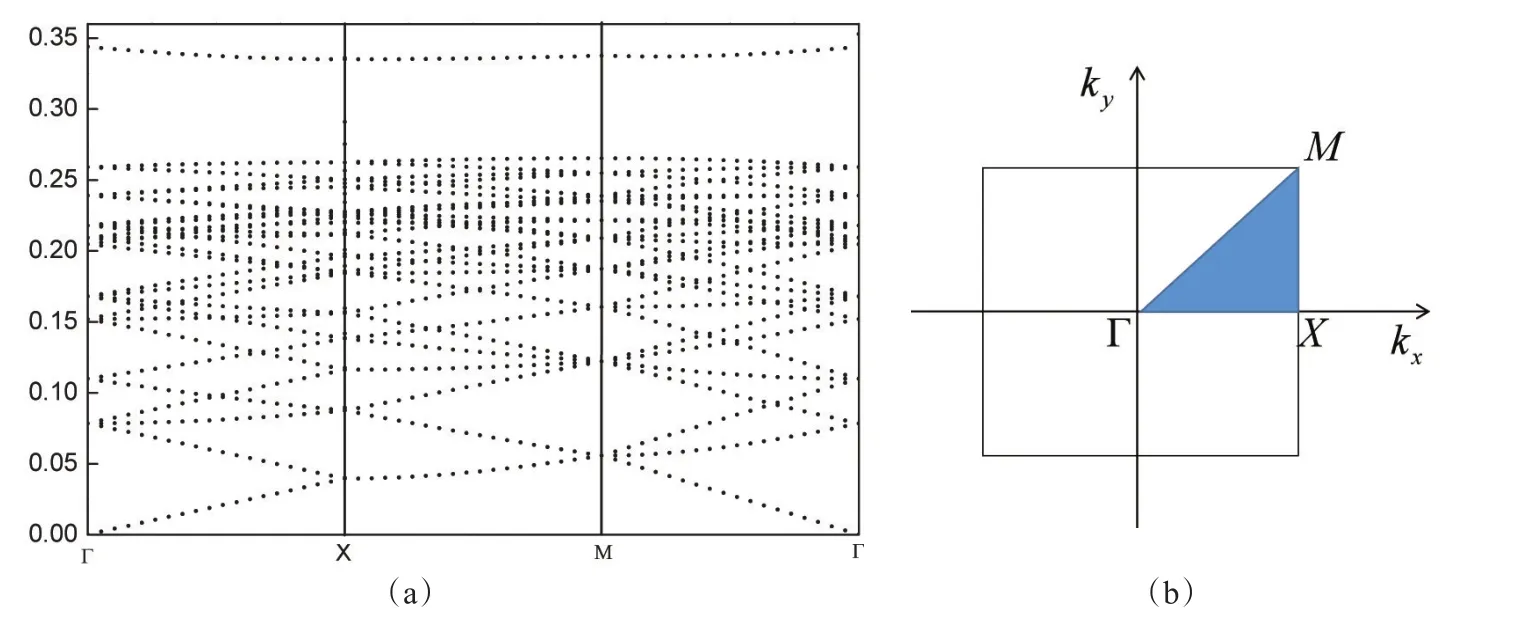
圖2 （a）完整正方結構二維光子晶體的帶隙結構；（b）正方結構二維光子晶體第一布里淵區的擴展圖

為了破壞完整光子晶體的周期性得到禁帶中某一頻率的光，我們引入點缺陷。在二維函數光子晶體[15-18]相關研究的基礎上，為了進一步簡化光子晶體的制作過程，周圍光子晶體保持為常規不變，缺陷處介質柱介電常數為空間坐標分布的函數，進一步研究點缺陷介質柱介電常數中可調參數k的變化對光子晶體帶隙結構的調節作用。圖3為正方結構含兩個點缺陷的二維光子晶體的帶隙結構和本征場分布，其中，介質柱半徑ra=0.3a保持不變，可調參數k=7.8×107m-1，參數b=9，即相對介電常數εr=7.8×107r+9。

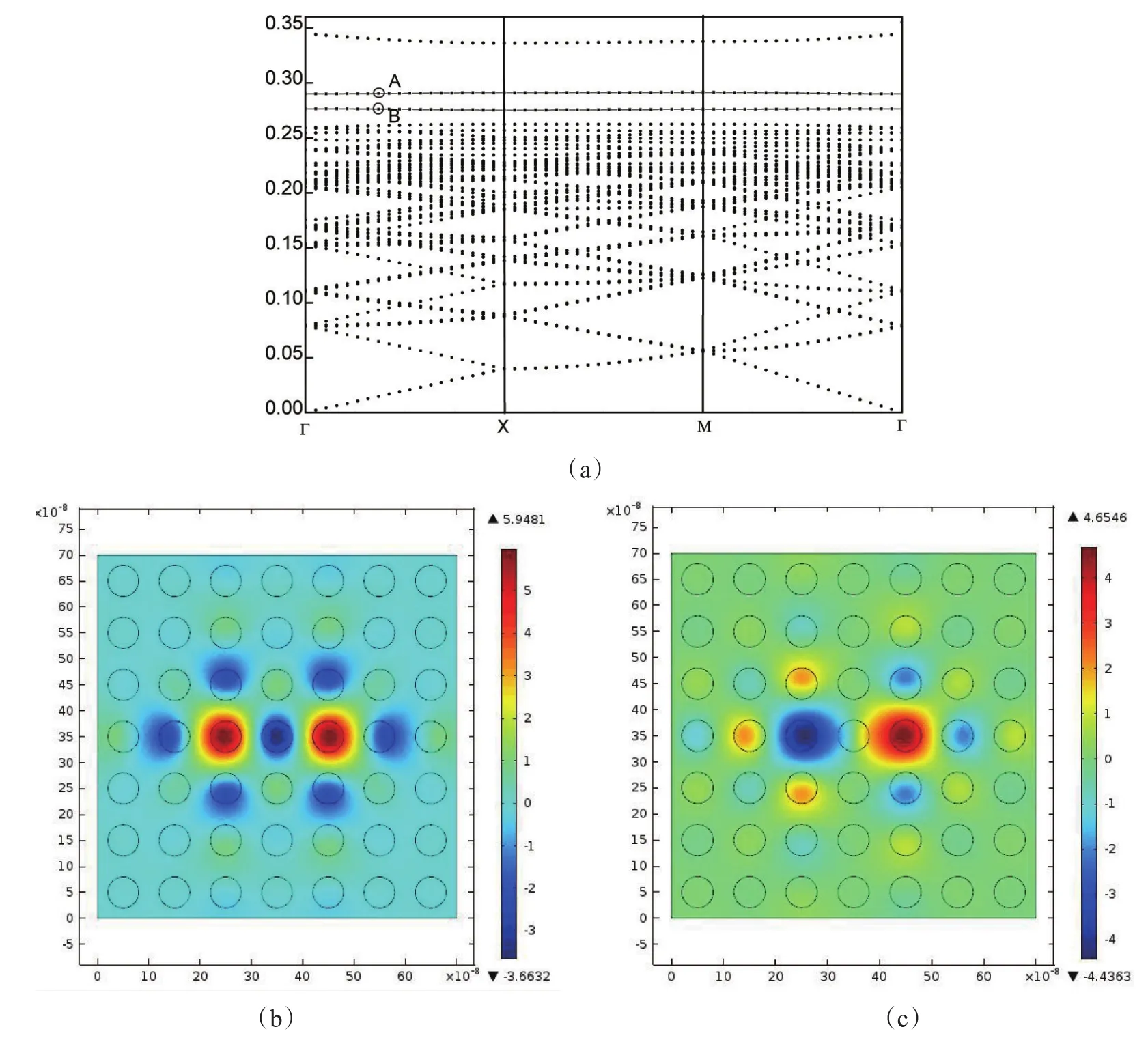
圖3 （a）含缺陷光子晶體帶隙結構圖（k=7.8×107m-1）；（b）A點對應的本征場圖；（c）B點對應的本征場

在圖3（a）中，歸一化頻率為0.26～0.34中出現了兩條缺陷模。在兩條缺陷模上分別取點A坐標為（0.315 8，0.290 2）和點B坐標為（0.315 8，0.276 2），對應歸一化頻率在Ez方向的本征場分別為圖3（b）、（c），右側彩虹條表示場強的強弱，由上至下場強呈遞減趨勢。由圖3（b）知，在兩個缺陷位置電場強度很強，呈現偶對稱形式分布，在遠離缺陷位置電場強度變弱。當光子晶體周期結構被破壞，光子被局限在缺陷處時，能量不斷聚集，因此缺陷處場強越來越大，遠離缺陷處，場強越來越小。在圖3（c）中，右側缺陷模處電場強度很強，左側缺陷處電場強度很弱，呈現奇對稱分布，此時光的能量可以集中分布在右側缺陷處，而左側電場強度很弱。

在圖4中，介質柱半徑ra和參數b不變，可調參數k=1.58×108m-1，即點缺陷介質柱的相對介電常數εr=1.58× 108r+9，其對應的帶隙結構和本征場分布對應于圖4（a）和4（b）。在圖4（a）中，歸一化頻率0.26～0.34中出現了一條缺陷模，相比于圖3，缺陷模的位置紅移，且模數減少。在缺陷模上取點A坐標為(0.315 8，0.273 3)，對應歸一化頻率在Ez方向的本征場為圖3（b），在兩個缺陷位置電場強度很強，呈現偶對稱形式分布，在遠離缺陷位置電場強度變弱。

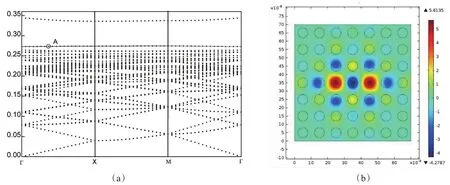
圖4 （a）含缺陷光子晶體帶隙結構圖（k=1.58×108m-1）；（b）A點對應的本征場圖

在圖5中，介質柱半徑ra和參數b不變，可調參數k=3.08×108m-1，即點缺陷介質柱的相對介電常數為εr=3.08× 108r+9，其對應的帶隙結構為圖5（a）。在圖5（a）中，在歸一化頻率為0.26～0.3禁帶中，缺陷模消失。缺陷模消失與圖2所示的完整結構光子晶體帶隙結構相同，即通過調節點缺陷介質柱介電常數中可調參數k可得到與完整光子晶體相同的帶隙結構。

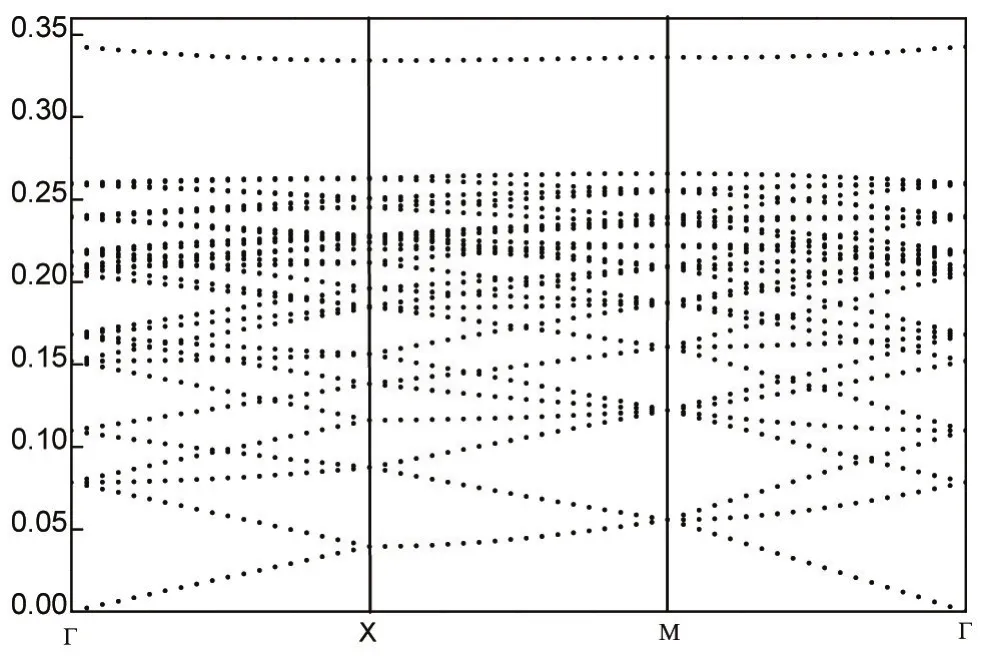
圖5 含兩個點缺陷的二維光子晶體的帶隙結構（k=30.8×107m-1）

比較圖3～5可知，當點缺陷介質柱介電常數中可調參數k增大時，缺陷模的數目減小，位置紅移。可調參數k的變化，通過改變外加電場的大小和分布形式來實現，即可以通過改變外加電場的方式，方便地調節二維光子晶體的帶隙結構，控制缺陷模的數量和位置，從而得到所需的帶隙結構。

3 結論

綜上所述，通過理論推導介質柱介電常數為空間坐標函數形式的Fourier積分解析表達式，用COMSOL仿真軟件模擬得到二維光子晶體的帶隙結構和電場分布。結果表明：當點缺陷介質柱介電常數中可調參數k增大時，缺陷模的數目減小，位置紅移，從而可以通過改變點缺陷介質柱介電常數中可調參數k的值，實現二維光子晶體的帶隙結構的調制。可調參數k的變化，可依據電光效應，通過改變外加電場的大小和分布形式來實現。由于點缺陷介質柱的介電常數的函數系數可調節，其得到的帶隙結構也可調節，因此可以得到所需要的帶隙結構。這為光學器件的設計提供了理論基礎和新的設計思路。相比于常規光子晶體，不需要重新更換介質柱，這也會節省大量的材料成本。