冶金法提純多晶硅退火工藝優(yōu)化的數(shù)學(xué)模型分析與試驗(yàn)驗(yàn)證
朱徐立 徐 隆 蘇 騎 吳虹瓊
(1 廈門城市職業(yè)學(xué)院機(jī)械與自動(dòng)化工程系,廈門 361000)
(2 美甘齊動(dòng)(廈門)物料輸送工程股份有限公司,廈門 361000)
(3 廈門理工學(xué)院軟件工程學(xué)院,廈門 361000)
文 摘 冶金法制備多晶硅過程中,通過對(duì)不同退火溫控方案進(jìn)行數(shù)學(xué)建模,探求優(yōu)化的退火理論溫度控制函數(shù)與曲線。數(shù)學(xué)模型表明,對(duì)硅鑄錠直接進(jìn)行保溫,依靠自然熱平衡退火,會(huì)使內(nèi)部應(yīng)力大于產(chǎn)生位錯(cuò)的臨界應(yīng)力;采用加熱元件對(duì)硅鑄錠適當(dāng)加熱保溫可減緩降溫速率。通過比較,選擇較低的退火溫度1 236℃和較短的退火時(shí)間8.52 ks作為試驗(yàn)退火溫控方案。試驗(yàn)驗(yàn)證表明,該退火方案得到的多晶硅鑄錠目視裂紋較少,少數(shù)載流子壽命與電阻率具有明顯優(yōu)勢。
0 引言
在冶金法(物理法)多晶硅鑄錠的提純中,多晶硅鑄錠內(nèi)部熱應(yīng)力的大小和分布與晶體缺陷息息相關(guān),是影響產(chǎn)品質(zhì)量的關(guān)鍵因素,并最終影響光電轉(zhuǎn)換效率。通過溫控進(jìn)行熱應(yīng)力的控制涵蓋了定向凝固與退火全過程,退火過程的工藝甚至對(duì)鑄錠的成功與否起決定性作用。定向凝固完成后,如不作任何熱處理,直接放由鑄錠爐的爐溫自然降至室溫拆爐,硅鑄錠內(nèi)部冷熱不均現(xiàn)象嚴(yán)重,上下表面的溫度差異很大,可達(dá)380~430℃[1],造成熱應(yīng)力增大[2-3],極有可能產(chǎn)生大量位錯(cuò),甚至使鑄錠碎裂[4-5]。因此,合理而周全的退火措施是保證鑄錠成功的必要手段,進(jìn)而減少熱脹冷縮現(xiàn)象,不但能避免裂錠,還能改善晶體生長和排列條件,在一定程度上降低位錯(cuò)概率。
退火工藝因定向凝固爐的不同而各異,大多數(shù)需要依據(jù)經(jīng)驗(yàn)通過多次試驗(yàn)或試生產(chǎn)來制定[6-7]。對(duì)多晶硅鑄錠退火過程的理論研究多是進(jìn)行定性分析,而定量分析特別是退火過程的數(shù)學(xué)模型方面的研究還比較少,本文通過建立數(shù)學(xué)模型,可以方便地改變工藝參數(shù),尋求合適的工藝方案,對(duì)減少試驗(yàn)次數(shù)、指導(dǎo)生產(chǎn)實(shí)踐和降低成本有著重要的理論依據(jù)和參考價(jià)值。
1 數(shù)學(xué)建模
從節(jié)能、控制簡便與降低熱應(yīng)力的角度出發(fā),提出以下兩種退火溫控工藝進(jìn)行數(shù)學(xué)建模分析:第一種退火工藝是在定向凝固結(jié)束后,在硅鑄錠頂部、底部、側(cè)壁均進(jìn)行良好的絕熱保溫,使鑄錠內(nèi)部溫度自然平衡達(dá)到一致的退火溫度后,再緩慢降溫至室溫(該方案主要作為參照目的);第二種退火工藝是凝固完成后,利用爐體安裝的加熱元件,對(duì)硅鑄錠進(jìn)行適當(dāng)補(bǔ)熱,使鑄錠內(nèi)部熱平衡過程更加舒緩。
1.1 針對(duì)第一種退火工藝的建模
退火工藝過程的數(shù)學(xué)描述為:設(shè)凝固完成后時(shí)間點(diǎn)τ=0,此時(shí)硅鑄錠頂部初始溫度為ta0,底部初始溫度為tb0,由于凝固完成,相變過程結(jié)束,沒有內(nèi)熱源產(chǎn)生,高低溫面的熱傳導(dǎo)使退火溫度tAnn介于ta0與tb0之間,因此,硅鑄錠中必存在一個(gè)t=tAnn的等溫面SAnn,并設(shè)該面高度為yAnn(圖1)。
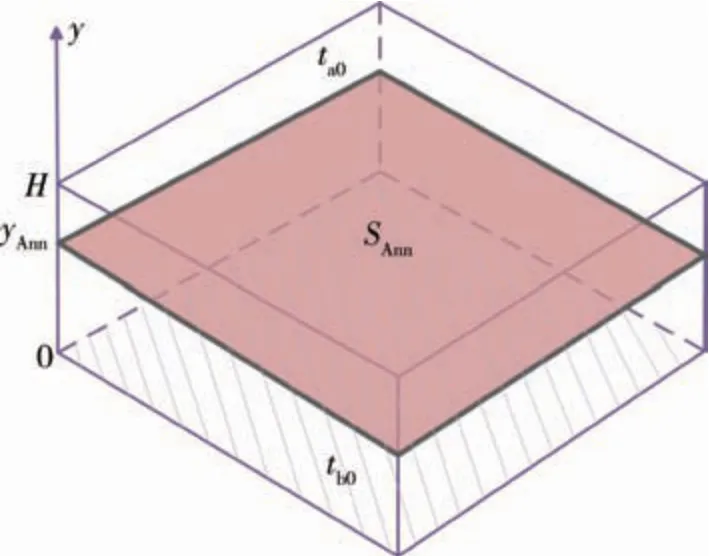
圖1 退火初始溫度分布Fig.1 Distribution of initial annealing temperature
由于ta0降至tAnn與tb0升至tAnn的時(shí)間相等,該過程滿足一維瞬態(tài)熱傳導(dǎo)微分方程,有

式中,a為熱擴(kuò)散系數(shù)。
滿足邊界條件
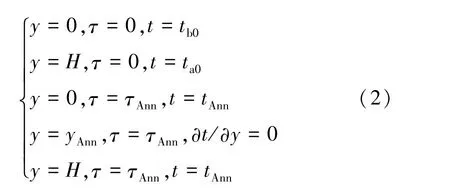
式中,τAnn為退火時(shí)間;H為硅鑄錠高度;λ為硅鑄錠熱導(dǎo)率。
1.2 針對(duì)第二種退火工藝的建模
從緩解退火過程中的熱應(yīng)力考慮,凝固完成后,用爐內(nèi)加熱元件對(duì)硅鑄錠適當(dāng)補(bǔ)熱,使鑄錠溫度趨于一致的過程放緩,同時(shí)退火溫度得到提高。設(shè)該補(bǔ)熱功率為qa,該過程的數(shù)學(xué)描述同式(1),僅邊界條件改變?yōu)?/p>
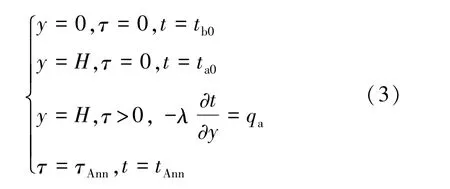
2 數(shù)學(xué)模型求解與討論
2.1 第一種退火工藝數(shù)學(xué)模型求解
求解偏微分方程(1),除了式(2)定義的邊界條件,由文獻(xiàn)[8]可知,硅鑄錠內(nèi)部溫度分布沿y方向服從拋物線t(y)分布。由于ta0、tb0初始值一定,在良好絕熱條件下,熱平衡后的tAnn為唯一確定值。對(duì)式(1)采用拉普拉斯(Laplace)變換,有
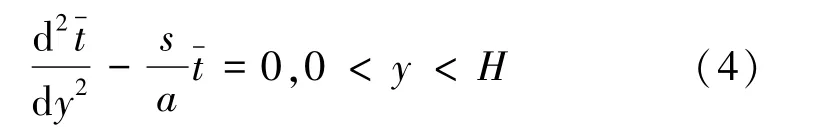
式中,s為Laplace算子。
式(4)的解為

查拉普拉斯變換表[8],經(jīng)過拉氏反變換,得到式(1)的解,有
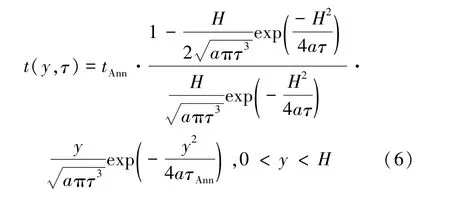
于是得到退火溫控方案1的數(shù)學(xué)表達(dá)式。
2.2 第二種退火工藝數(shù)學(xué)模型求解
同理,可求解式(1)(3),得到的解見式(7)。
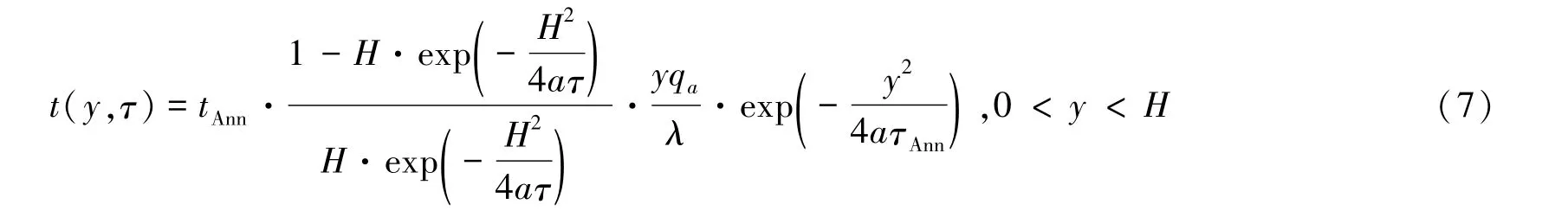
不同的是,式(6)只需要代入ta0、tb0、H等待定的已知條件,即可推導(dǎo)出該條件下tAnn和τAnn的值,而式(7)不但包含上述待定值,還包括補(bǔ)熱功率qa這個(gè)待定參數(shù),且tAnn和τAnn均為qa的函數(shù),求解式(7)需要試算大量的qa值,過程繁瑣。因此可以基于式(7)利用圖像法求解。以ta0=1 400℃,tb0=1 000℃,H =0.5 m為例,可繪制qa關(guān)于tAnn和τAnn的函數(shù)圖像,圖2中,tAnn曲線與τAnn曲線分別有‘2’、‘3’兩個(gè)交點(diǎn),即得到兩個(gè)退火方案。方案2:tAnn=1 236℃,τAnn=8.52 ks,qa=5.9 kW;退火溫控方案3:tAnn=1 351℃,τAnn=11.283 ks,qa=10.3 kW。
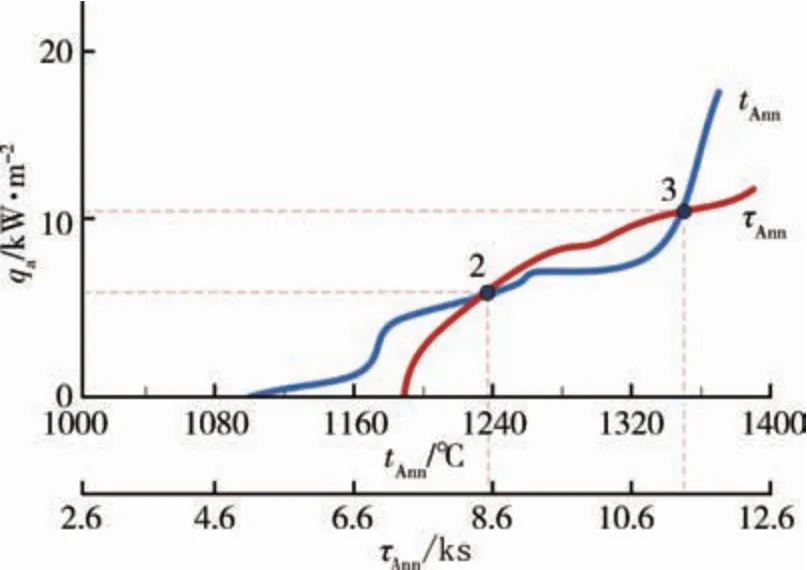
圖2 退火溫度與退火時(shí)間的函數(shù)關(guān)系Fig.2 Function relation between annealing temperature and annealing time
2.3 求解結(jié)果討論
綜合文獻(xiàn)[9-10]的研究和工程經(jīng)驗(yàn),認(rèn)為多晶硅晶體內(nèi)部區(qū)域應(yīng)力>16.5 MPa時(shí),該區(qū)域出現(xiàn)大量位錯(cuò)的概率較大,當(dāng)應(yīng)力≥42 MPa時(shí),則極可能出現(xiàn)可見的明顯裂紋。本文將16.5 MPa作為硅鑄錠許用應(yīng)力臨界值,因此,tAnn與τAnn的取值均受許用應(yīng)力(16.5 MPa)的約束,退火過程的熱應(yīng)力必須低于該值。
在第一種退火工藝中,同樣令ta0=1 400℃,tb0=1 000℃,H=0.5 m,代入式(6)求解得tAnn=1 118℃,τAnn=6 980 s,作為退火溫控方案1。在ProE軟件中進(jìn)行建模,硅鑄錠寬度W =1 m,H =0.5 m,導(dǎo)入有限元軟件的Transient Thermal與Structural模塊進(jìn)行計(jì)算,設(shè)置計(jì)算參數(shù)與邊界條件:多晶硅的楊氏模量E =190 GPa,剪切模量G =89 GPa,泊松比μ=0.172,以 tAnn=1 118℃為計(jì)算終了溫 度,以τAnn=6.98 ks作為計(jì)算時(shí)長,求解熱應(yīng)力,獲得退火全程鑄錠最大熱應(yīng)力的變化曲線(圖3)。

圖3 退火過程中硅鑄錠應(yīng)力變化曲線(方案1)Fig.3 Stress variation curves during annealing in silicon ingot(method 1)
很明顯,圖3中大部分時(shí)間內(nèi),熱應(yīng)力已超過臨界值(16.5 MPa),最大熱應(yīng)力值為23.8 MPa。硅錠依靠自然熱平衡進(jìn)行退火,熱應(yīng)力較大,有大概率形成大量位錯(cuò),甚至裂紋,該方案在理論上不可取。
同樣的,對(duì)退火溫控方案2和3進(jìn)行數(shù)值分析,所獲得的熱應(yīng)力變化曲線見圖4。
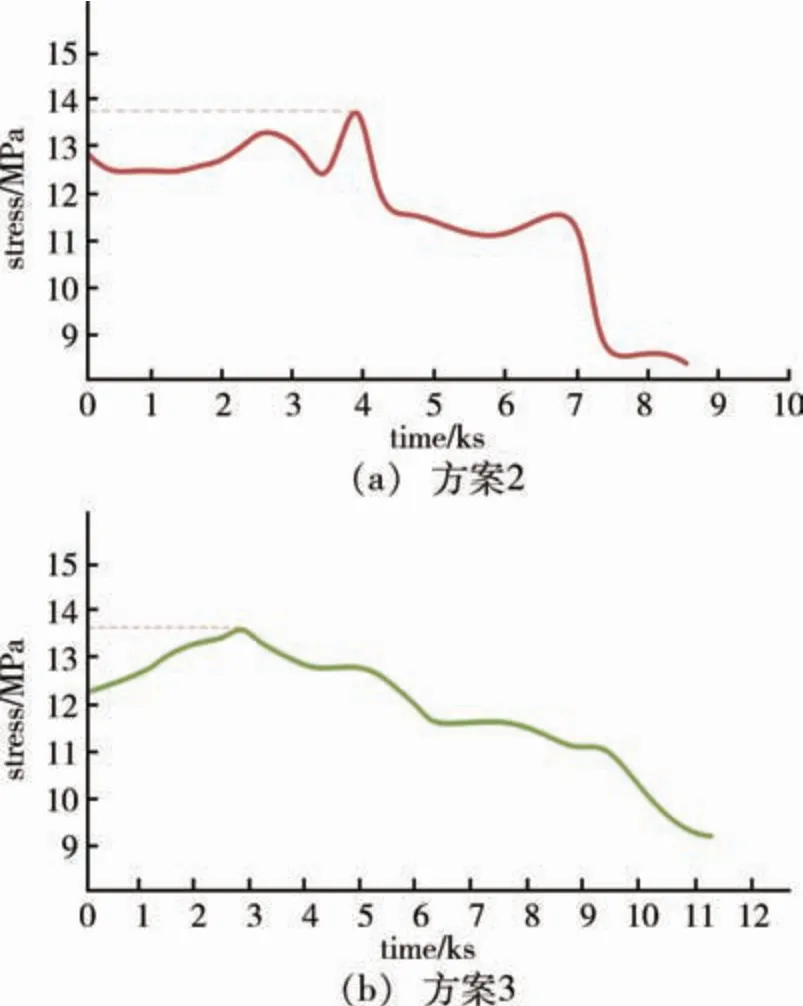
圖4 退火過程中硅鑄錠應(yīng)力變化曲線Fig.4 Stress variation curves during annealing in silicon ingot
圖4可以看出,方案2產(chǎn)生的最大熱應(yīng)力為13.72 MPa,方案3為13.6 MPa,均未超出臨界值。將以上3種求解結(jié)果匯總于表1。
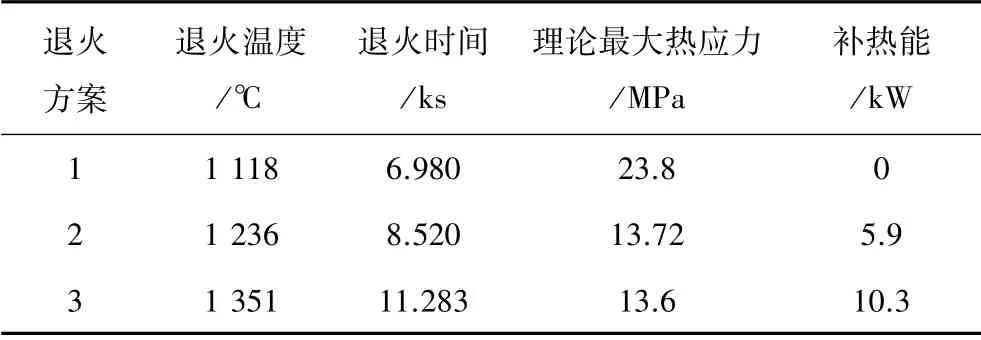
表1 三種求解結(jié)果的比較Table.1 Comparison of three solution results
一般來說,延長退火時(shí)間可以減少熱應(yīng)力,但過長的退火時(shí)間會(huì)降低生產(chǎn)效率,同時(shí)也增加能耗。雖然方案2的最大熱應(yīng)力略大于方案3,但退火時(shí)間和能耗明顯降低,因此方案2為比較合理的理論退火方案。
3 實(shí)驗(yàn)
實(shí)驗(yàn)采用3N級(jí)多晶硅原料,使用本課題所研發(fā)的環(huán)形加熱鑄錠爐[11]進(jìn)行鑄錠與提純。在凝固完成后分別采用上述方案1~3進(jìn)行退火,比較所鑄造的硅錠并檢測主要指標(biāo)。
3.1 實(shí)驗(yàn)結(jié)果
定向凝固結(jié)束后,經(jīng)歷3種不同退火方案后,得到的硅鑄錠剖面如圖5所示。可以看出,有貫穿硅鑄錠上下底面的深層裂紋(退火方案1);采用退火方案2,沒有明顯的目視裂紋;而退火方案3在剖面右半部分則出現(xiàn)了局部淺表性裂紋。

圖5 硅鑄錠剖面Fig.5 Section of silicon ingot
3.2 分析與討論
通過理論計(jì)算可知方案2、3全過程硅鑄錠的熱應(yīng)力均未超過臨界值,但在退火過程末期[圖4(a)時(shí)間≥7 ks],方案2的熱應(yīng)力曲線有明顯的大幅下降,因此,退火方案2對(duì)退火過程末期有更好地應(yīng)力疏解作用。按照理論計(jì)算,退火方案3熱應(yīng)力不超過臨界值,但得到的硅鑄錠則產(chǎn)生了明顯的淺表性裂紋,經(jīng)過分析,推測造成退火方案3中硅鑄錠出現(xiàn)裂紋的可能原因有以下兩種。
(1)試驗(yàn)使用的本課題研發(fā)的鑄錠爐(參見文獻(xiàn)[11]中圖7),該爐采用的是加熱裝置環(huán)形布置的方案,根據(jù)文獻(xiàn)[11]的研究,為了節(jié)能和加強(qiáng)定向凝固時(shí)的對(duì)流傳質(zhì),加熱裝置并未全面均勻布置。但由于硅鑄錠本身熱惰性的存在,在退火時(shí)間較長的情況下,環(huán)形加熱形成的補(bǔ)熱熱場與理論情形(一維熱場,溫度梯度垂直向上)有一定偏差,造成對(duì)熱應(yīng)力的疏解較弱。
(2)溫度傳感器設(shè)置于鑄錠爐上、下表面及側(cè)壁位置(硅鑄錠內(nèi)部無法布置任何傳感器),方案3的補(bǔ)熱強(qiáng)度很大,在退火時(shí)間較長的情況下,根據(jù)傳感器采集到的信號(hào),自動(dòng)控制系統(tǒng)“誤認(rèn)為”硅錠整體已經(jīng)達(dá)到溫度均勻,進(jìn)而停止補(bǔ)熱,而此時(shí)硅鑄錠并未達(dá)到溫度均勻,內(nèi)部熱應(yīng)力還比較大。
通過在硅鑄錠剖面上鉆孔取樣,取4個(gè)取樣點(diǎn)(Sampling points)的檢測值平均,作為該鑄錠的檢測指標(biāo),得到不同退火方案下的硅鑄錠主要指標(biāo)見表2。

表2 不同退火方案硅鑄錠檢測指標(biāo)Table.2 Testing index of silicon ingot with different annealing schemes
由表2可知,不同的退火方案下,磷、硼以及主要金屬雜質(zhì)的含量基本相同,這是由于提純雜質(zhì)主要依靠定向凝固過程的分凝效應(yīng)[12]實(shí)現(xiàn),退火過程對(duì)雜質(zhì)提純影響極小。方案2的少數(shù)載流子壽命和電阻率指標(biāo)最優(yōu),說明退火處理減小熱應(yīng)力有利于上述兩種指標(biāo)的提高。此外,方案1采用自然降溫退火,因此能耗值最低,方案2、3采用補(bǔ)熱退火,能耗均高于方案1,其中,方案3退火時(shí)間最長,能耗最高。
4 結(jié)論
經(jīng)過對(duì)退火工藝的數(shù)學(xué)建模與求解,得到如下成果與結(jié)論:定向凝固完成后,須經(jīng)歷退火過程以降低硅錠頂、底面溫差造成的內(nèi)部熱應(yīng)力,經(jīng)過理論推導(dǎo),獲得3種退火溫控方案:tAnn=1 118℃,τAnn=6.98 ks;tAnn=1 236℃,τAnn=8.52 ks,qa=5.9 kW 以及tAnn=1 351℃,τAnn=11.283 ks,qa=10.3 kW。從熱應(yīng)力控制、節(jié)能和提高生產(chǎn)率的角度考慮,方案2在理論上比較合理。通過實(shí)驗(yàn),該退火方案得到的多晶硅鑄錠目視裂紋最少,少數(shù)載流子壽命與電阻率則明顯優(yōu)于方案1和方案3。本文推導(dǎo)的數(shù)學(xué)模型可以采用不同工藝參數(shù)代入求解,為冶金法提純多晶硅的退火工藝的制定提供重要的理論參考。

