基于遞推最小二乘法的轉向系統參數辨識
李 偉,王洪民,唐 崢
(重慶交通大學 機電與車輛工程學院,重慶 400074)
0 引 言
轉向系統是控制汽車按指定路線和方向行駛的重要裝置,精確的物理參數在對建立車輛系統動態數學模型和分析中起著至關重要的作用[1]。針對系統的參數辨識,比較主流的辨識方法有模型自適應辨識算法[2]、最小二乘法[3-4]、擴展卡爾曼濾波法[5-6]、遺傳算法[7]、掃頻測試等。其中擴展卡爾曼濾波法的P、Q矩陣很難確定,而且與系統狀態密切相關;遺傳算法對待估參數初值要求較高;掃頻測試需要用不同的頻率去激勵系統,再用最小二乘法求得閉環系統的幅頻特性與相頻特性,最后利用MTLAB的INVFREQS函數進行擬合,這種算法采集到的數據不僅不多,而且還要進行兩次擬合,會造成辨識出的參數結果精度不高;加之遺傳算法和掃頻測試也不能做到參數在線實時估計。宗長富等[8]采用最小二乘法與遺傳算法相結合的方法以TruckSim數據為基礎離線辨識出了商用車三自由度模型的前軸側偏剛度、后軸側偏剛度、側傾阻尼和側傾剛度4個關鍵參數,并繪制出辨識出參數的MAP圖,代入數學模型進行仿真驗證。結果表明:該方法能較準確辨識出系統模型的關鍵參數,關鍵參數MAP圖能實時準確表征車輛的實時動態特性,為商用車參數估計和穩定性控制奠定了良好基礎。李凌陽[9]對車輛懸架系統的進行參數辨識研究,分別采用對數衰減法、頻域法和面積法來辨識懸架系統的阻尼比,并利用系統模型辨識出車輛的簧上和簧下質量,對于研究懸架主動控制策略具有非常重要的意義。
首先利用MATLAB進行遞推最小二乘法仿真,結果表明,該方法能夠快速有效準確地估計出系統參數;然后MicroAutoBox發出PWM波控制P-EPS驅動版中“H”橋中4個功率晶體管的通斷,利用博世傳感器采集轉向系統中方向盤的轉角,系統的輸入電流由驅動板采集,根據采集的電流和轉角編寫遞推最小二乘法,對未知轉向系統的有關參數進行在線估計。
1 遞推最小二乘法原理
考慮如下受控自回歸(controlled autoregressive,CAR)模型:
A(z-1)y(k)=B(z-1)u(k-h)+ξ(k)
(1)
式中:u(k)為白噪聲;ξ(k)和y(k)分別為系統的輸入輸出;h為已知數,且
式中:na、nb為結構參數并已知。
參數估計的任務是根據可測量的輸入和輸出,確定如下na+nb+1個參數:
a1,a2,…ana;b0,b1,b2,…,bnb
對式(1)寫成如下最小二乘法格式:
y(k)=-a1y(k-1)-…-anay(k-na)+b0u(k-d)+…+bnbu(k-d-nb)+ξ(k)=φT(k)θ+ξ(k)
式中:φ(k)為數據向量;θ為待估參數向量,且:

(2)
式中:
設k時刻最小二乘估計為
(3)
式中:
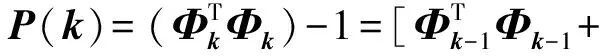
φ(k)φT(k)]-1=[P-1(k-1)+φ(k)φT(k)]-1
則:P-1(k)=P-1(k-1)+φ(k)φT(k)
(4)
(5)
則由式(4)和式(5)可得:
于是k時刻的最小二乘估計可表示為
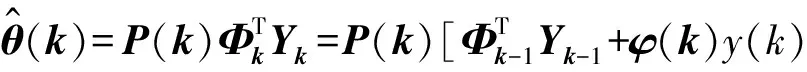
(6)
式中:
K(k)=P(k)φ(k)
(7)
根據矩陣求逆原理,設A、(A+BC)和(I+CA-1B)均為非奇異方陣,則
(A+BC)-1=A-1-A-1B(I+CA-1B)-1CA-1
(8)
令A=P-1(k-1)、B=φ(k)、C=φT(k),得
P(k)=P(k-1)-P(k-1)φ(k)[1+φ(k)P(k-1)φ(k)]-1φT(k)P(k-1)
(9)
將式(9)帶入式(7),可得:
K(k)=P(k-1)φ(k)-
(10)
由式(9)和式(10)可得:
P(k)=[I-K(k)φT(k)]P(k-1)
(11)
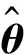
(12)
2 輸入信號的選擇
如果建立的系統數學模型結構選擇正確,則模型參數辨識的精度好壞將直接依賴于系統輸入信號,因此選用合理的輸入信號是保證能否獲得理想的辨識結果的關鍵因素之一。通過理論分析表明,選用白噪聲作為辨識輸入信號可以獲得較好的辨識結果,但這在工程上幾乎不易實現,因為實際工業設備不可能按白噪聲的變化規律動作。采用近似白噪聲的逆M序列代替白噪聲信號。
2.1 M序列定義
設有一個無限長的二元序列x1,x2, …,xp,xp+1,各元素間存在下列關系:
xi=a1xi-1⊕a2xi-2⊕…⊕apxi-p
式中:i=p+1,p+2,…;系數a1,a2,…,ap-1取值為0或1;系數ap總為1;⊕為異或運算符。
只要適當選擇系數a1,a2,…,ap-1,就可以使序列以(2p-1)bit的最長周期循環,這種具有最長循環周期的二元序列稱為M序列。
M序列它具有近似白噪聲的性質,是一種很好的系統辨識輸入信號。其主要性質有:
1)均衡性。在M序列一個周期中,1的個數比0的個數要多1位,這表明該序列平均值很小。
2)M序列有良好的自相關性。
3)M序列發生器中移位寄存器的各種狀態,除了全0狀態外,其他狀態只在M序列中出現一次。
2.2 逆M序列
由譜分析表明,M序列通常含有直流成分,可能會造成辨識系統的“凈擾動”,這通常是我們不希望的。而逆M序列可以克服這一缺點,是一種比M序列更為理想的偽隨機碼序列。
設M(k)是周期為Npbit、元素取值為0或1的M序列,S(k)是周期為2bit、元素依次取值為0或1的方波序列,將這兩個序列按位進行異或運算,得到的復合序列就是周期為bit、元素取值為0或1的逆M序列,記作{IM(k)},即有:
{IM(k)}={M(k)}⊕{S(k)}
將上述逆M序列的邏輯值“0”或“1”分別換為-1或1,此時逆M序列均值為0。
雖然逆M序列是M序列與方波序列簡單復合的結果,但其性質卻優于M序列,使它在辨識領域中有著更加廣泛的應用。
3 仿真與分析
已知有如下三階系統的傳遞函數模型:
(13)
需要辨識的系統參數有2、50、100、10。取采樣時間為0.1 s,采用后向差分法即:
(14)
由式(13)和式(14)可以得出:
(15)
將式(15)寫成CAR形式:
(16)
這里模擬采集數據時有白噪聲的誤差干擾,因此將式(16)修正為
(17)
式中:ξ(k)為方差為1的白噪聲;u(k)為取值為1,-1的逆M序列。
這里只要辨識出-39/18、16/9、-5/9、1/180就可以由式(15)反推出三階系統中的各個參數。式(17)中參數辨識的精度可以反映式(13)中參數的精度。對式(17)編寫最小遞推最小二乘算法,其辨識結果如表1。
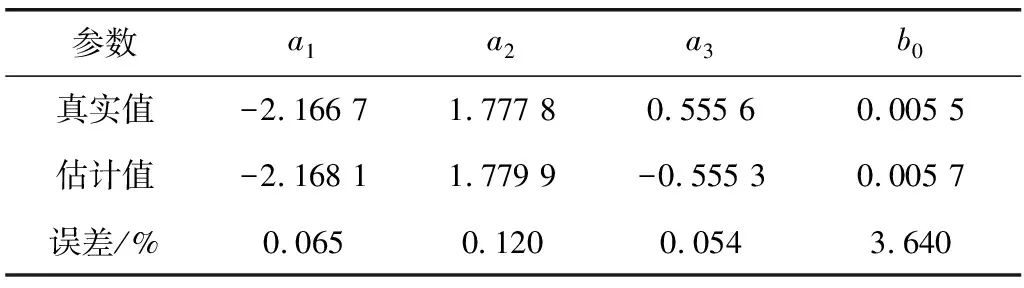
表1 參數辨識結果Table 1 Parameter identification results
從表1可以看出,前面3個參數的估計相對誤差都在0.2%以內,而最后一個參數由于本身數值特別小,但通過遞推最小二乘法可以準確估算到千分位,相對誤差也控制在4%以內。并且隨著所取數據的不斷增大,系統辨識的結果也會隨之改善。這就是遞推最小二乘法的一個優勢,可以根據不斷更新的數據,對前面所辨識的結果進行改善,使得辨識的結果更加接近真實值。
本次仿真采集10 000組數據,如圖1,可以觀測各個參數辨識的變化曲線,其中a1為-39/18的估計曲線、a2為16/19的估計曲線、a3為-5/9的估計曲線、b0為1/180的估計曲線、k為仿真步長。
綜上可以得出,遞推最小二乘法可以準確辨識出參數,辨識結果也比較理想。
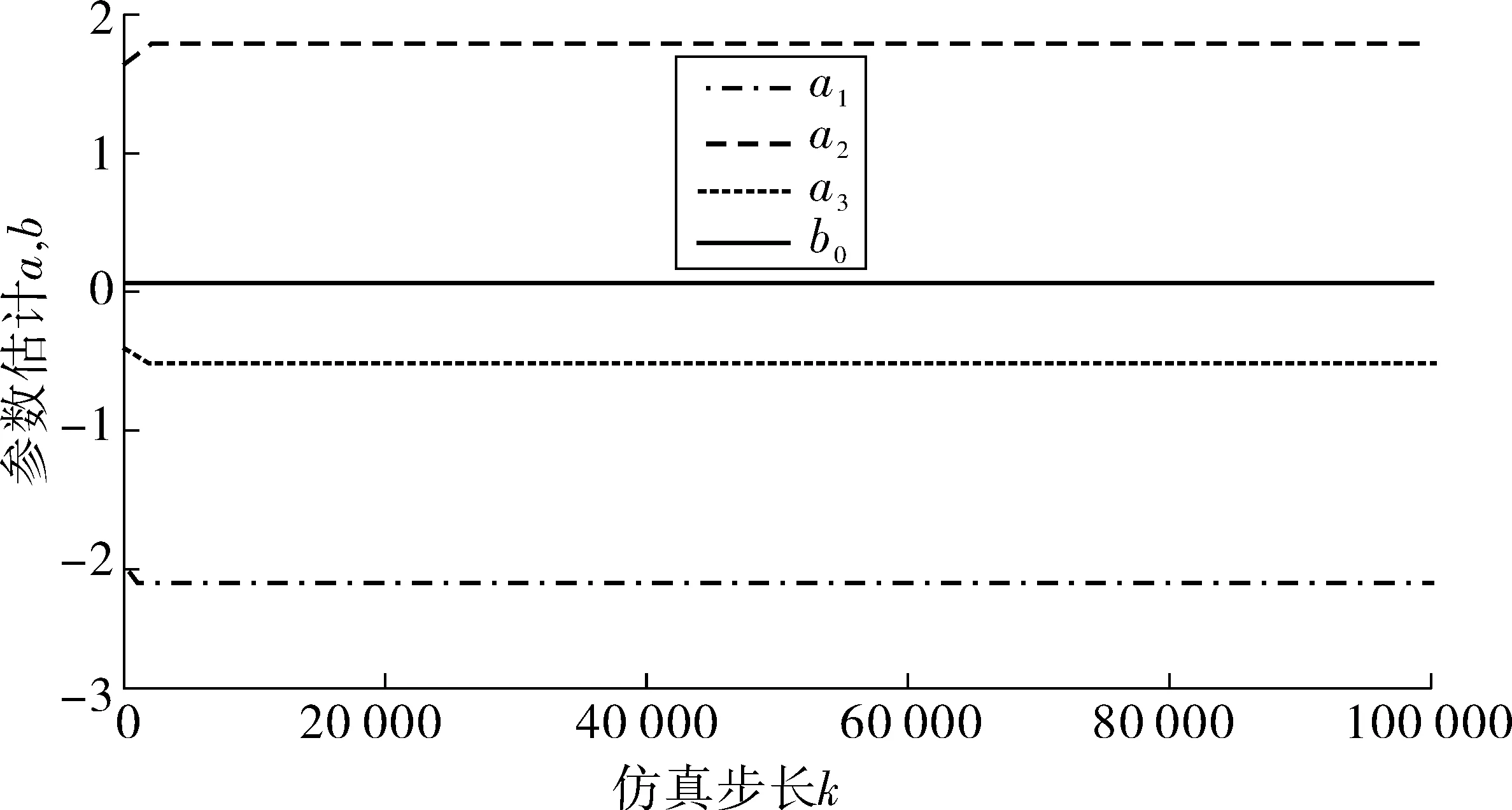
圖1 各估計參數的實時變化Fig. 1 Real-time changes of the estimated parameters
4 應用與推廣
轉向系統模型如式(18):
(18)
式中:J是等效到小齒輪上的轉動慣量;b是等效到小齒輪上的阻尼;km是等效到小齒輪上的剛度;kI是力矩系數;im是小齒輪傳動比;θ是方向盤轉角;i(t)是電機電流。
對式(14)進行拉普拉斯變換可得到轉向系統的傳遞函數為
(19)
這里采用后向差分法對式(15)進行離散化處理,取采樣時間為0.1 s,則有:
其中:
(20)
從而可以得到離散系統的表達式為
(21)
這里給電機輸入電壓為±4.8 V的逆M序列,i(k)為系統的輸入電流由驅動板采集,輸出轉角用博世傳感器進行采集。實驗基本框圖如圖2。
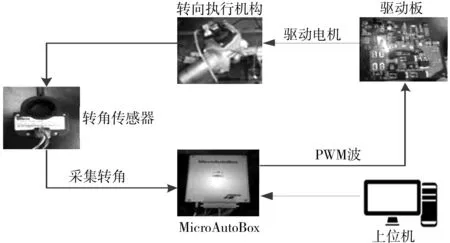
圖2 實驗基本框圖Fig. 2 Basic block diagram of the experiment
在MATLAB/Simulink軟件搭建電機驅動模型,并由dspace提供程序編譯環境,通過MicroAutoBox硬件輸出PWM波來控制驅動板中4個功率晶體管的通斷,來實現電機的調速功能,利用博世轉角傳感器對方向盤的轉角進行采集,由于該角度傳感器只接受ID為550 h的十六進制CAN報文,需要對采集到的數據進行破譯,這里可以利用dspace自帶的ControlDesk軟件用來記錄數據,此時記錄的數據是十進制的,不用在破譯。實驗平臺如圖3。

圖3 實驗平臺Fig. 3 Experimental platform
運行模型并用ControlDesk記錄博世角度傳感器采集的轉角數據,根據采集的輸出轉角及輸入電流,編寫遞推最小二乘法算法,實驗過程時,各參數的變化收斂如圖4,辨識結果為表2。
通過圖4可以實時在線觀測各參數的變化過程,也可以看出,遞推最小二乘法的收斂速度比較快,在k=500時,各個參數已趨于穩定。
式(18)中小齒輪傳動比im=18.75,用電機型式試驗自動測試系統測得電機的力矩系數kI=0.056 3,因此將參數估計值帶入式(20)可以解出轉向系統參數如表3。
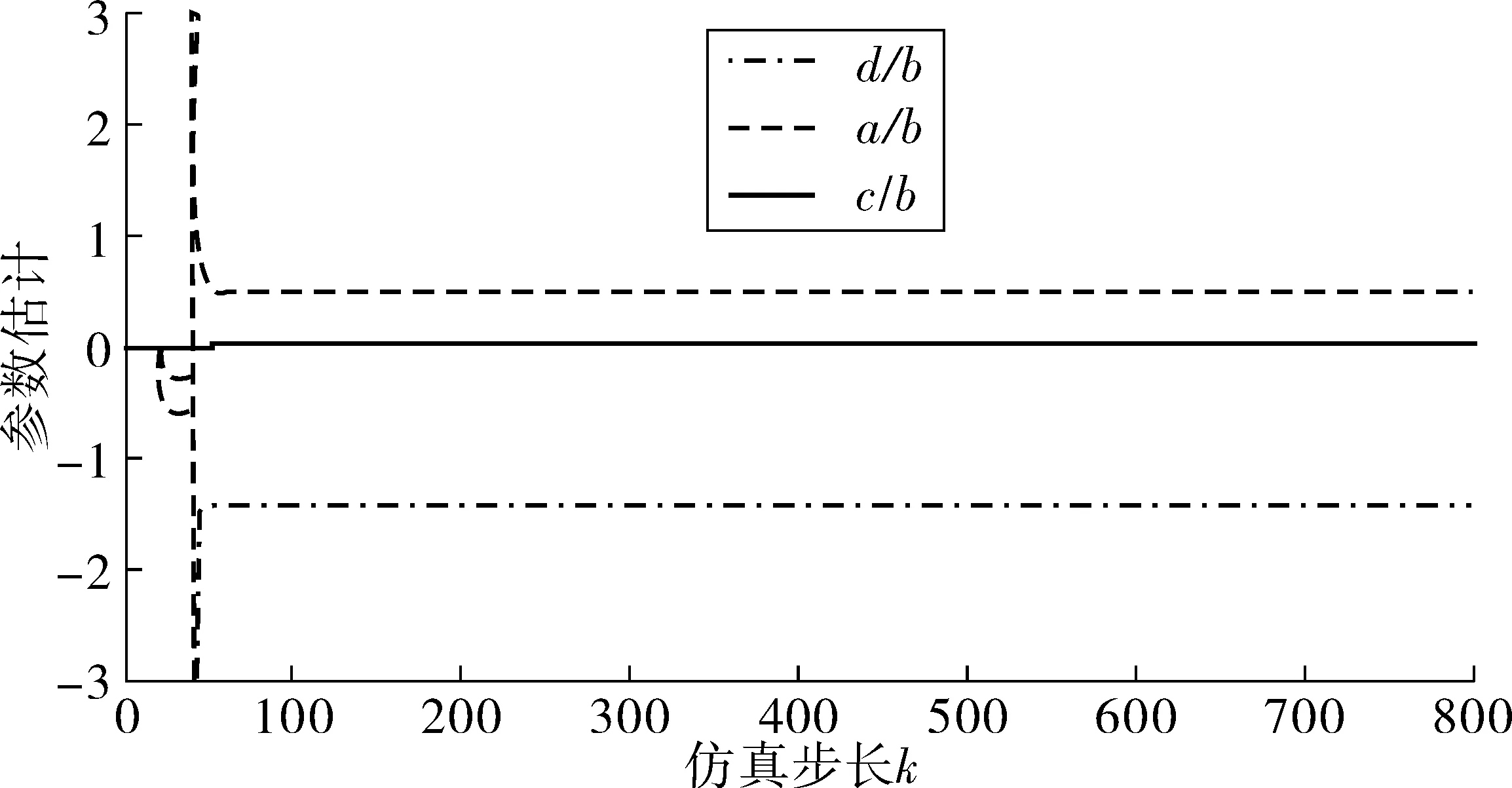
圖4 各參數的變化收斂過程Fig. 4 Convergence process of each parameter change

參數c/bd/ba/b參數估計值-1.425 90.540 20.044 1

表3 轉向系統參數Table 3 Steering system parameters
因此轉向系統的模型為
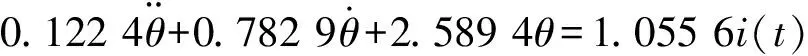
(22)
對辨識的參數進行驗證,驗證結果如圖5。
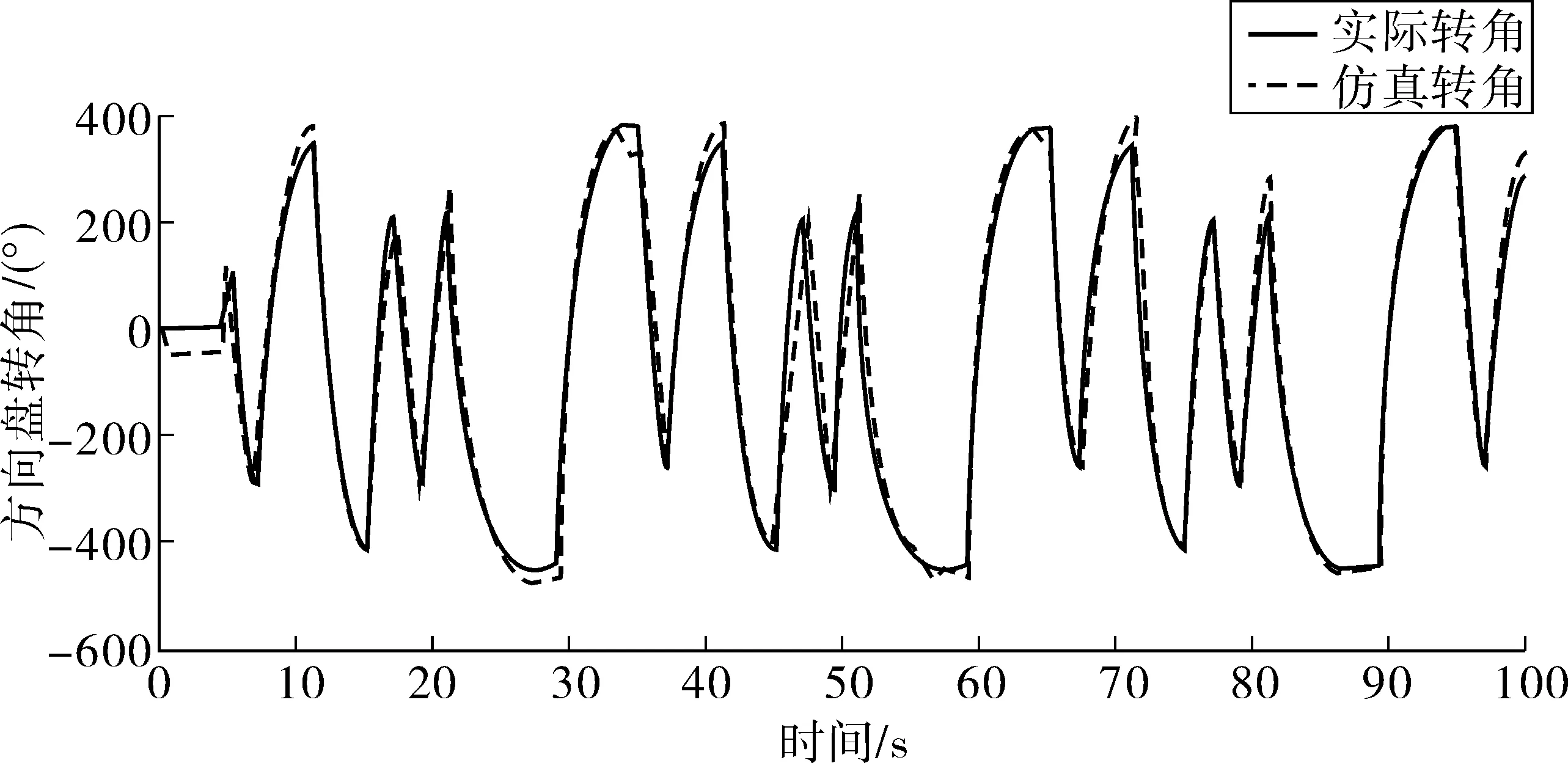
圖5 實際轉角與仿真轉角的對比Fig. 5 Comparison of actual corner and simulated corner
通過圖5可以看出,傳感器采集的實際轉角與通過辨識出來的參數的轉向系統模型仿真出的轉角非常相近,對辨識出的參數結果滿意。
5 結 語
根據表1仿真的結果表明,遞推最小二乘法可以快速準確的識別參數,參數辨識的精度也令人滿意。且在很多自適應控制系統中,被控對象通常都在不斷提供新的輸入輸出數據,而且希望能夠利用這些新信息來繼續改善參數估計的精度,遞推最小二乘法的在線實時估計能夠很好的解決這個問題。
筆者還將該算法應用到了汽車轉向系統上,辨識出了轉向系統的等效轉動慣量、等效阻尼系數、等效剛度,并對辨識出的參數進行了驗證,通過圖5可以看出驗證結果理想。此理論對未知系統參數辨識的研究具有重大意義。

