礦 物 顆 粒 度 對 粉 末 顏 色 的 影 響

王心華, 鐘 芬, 徐 躍, 許家奇

(蘭州大學 a. 物理學國家級實驗教學示范中心； b. 物理科學與技術學院， 蘭州 730000)

0 引 言

材料在研磨前后其顏色的變化受多種因素的影響，除了與其所用原材料的化學組分、材料類型、吸氧量、研磨溫度等一些因素有關外，研磨前后的粒徑分布也是其中的一個重要方面。在社會生活中，材料、能源、醫藥、冶金、化工、電子、機械、建筑及環保等諸多領域都與材料的粒度分布有關[1-5]。從礦物顏料顆粒度對色貌的影響這一角度出發， 基于光學角度，分析隨著顏料顆粒度的變化而導致的色彩屬性的變化，也可為文化遺產真實的數字化典藏、藝術品的高保真復制以及歷史文物色彩的真實虛擬再現提供理論支持。微米級別的礦物顆粒的許多性質與塊狀材料不同，研究其自然狀態下的性質具有一定的實際意義[6-10]。即使是相同的材料，微米顆粒與塊狀的在很多方面的特性也有一定的差異，因此，采用一般的針對塊狀材料的顏色測定方法來測定微米礦物顆粒顯然是不適用的。本文通過紫外-可見光譜儀測量粉末在一定范圍內的漫反射系數，并采用Mie散射理論，從光學角度研究同種顏料不同顆粒度下的明度、色調以及飽和度的變化，以為它不同的應用提供理論基礎。

1 基本理論

1.1 Mie理論[11]

Mie理論通過求解具有適當邊界條件的Maxwell 方程組，得到均勻球形粒子的光散射描述。在一定條件下，也可以求解非球形粒子(主要為圓柱形、橢球形的顆粒)以及顆粒內部折射率不均勻粒子的光散射。Mie理論通常研究的粒徑參數(x=2πr/λ)的范圍為1左右。

1.2 CIE色度圖[12]

國際照明委員會(Commission Internationale de L'Eclairage,CIE)制訂了一系列色度學標準，一直沿用到數字視頻時代，其中包括白光標準(D65)和陰極射線管(CRT)內表面紅、綠、藍3種磷光理論上的理想顏色。

2 實 驗

(1) 實驗原料。硅酸鋯ZrSiO4，氧化鐵Fe2O3，堿式碳酸銅Cu2(OH)2CO3，四氧化三鐵Fe3O4。

(2) 實驗設備。真空泵，行星式球磨機，X-射線衍射儀，Lambda950紫外-可見光譜儀，粒度分析儀。

(3) 實驗方法。本實驗采用球磨法制備不同粒徑的樣品[13-15]。每次稱取相應的粉末樣品12 g，裝罐，首先進行3 min的抽真空處理，隨后進行不同時間的球磨，最后取研磨不同時間后的樣品進行XRD測試以分析球磨前后材料物相的變化情況，測200～700 nm范圍內樣品的漫反射光譜并計算在可見光范圍內相對明度、色調及飽和度，以分析樣品在研磨前后顏色的變化情況。所得樣品分別為未研磨，研磨2、4、6 h。

3 結果與討論

3.1 XRD結果分析

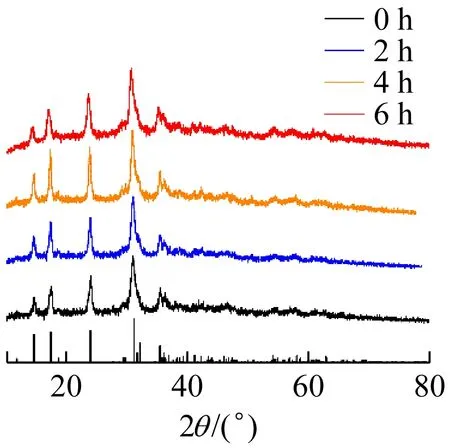
圖1為ZrSiO4、Fe2O3、Cu2(OH)2CO3、Fe3O4的不同研磨時間所對應的XRD圖。由圖1(a)可以看出，未研磨的硅酸鋯樣品與研磨2、4、6 h樣品的峰的位置相對應，強度也相同，且與國際標準卡片中該樣品的峰的位置與強度也相匹配。因此可以確定硅酸鋯樣品在研磨前后的物相并沒有發生改變，圖1(b)～(d)也呈現出相同的變化規律。因此可以得出結論，各材料在研磨前后的物相均未發生改變，可以排除由于物相的改變導致其顏色變化這一影響因素。

3.2 反射光譜曲線與粒徑分析

圖2為ZrSiO4、Fe2O3、Cu2(OH)2CO3、Fe3O4的不同研磨時間所對應的200～700 nm范圍內的漫反射光譜圖。

(c) Cu2CO3(OH)2

(a) ZrSiO4

(c) Cu2(OH)2CO3

本文引入視見函數這一概念[16]：人眼對紅、綠、藍響應的視錐細胞數量比約為32∶16∶1，所以，人眼對不同波長的單色光產生相同的視覺效應，要有不同的輻射功率；在引起相同的視覺響應條件下，若光波長為λ的光所需要的光輻射功率為P(λ),而對光波長為555 nm的光(人眼對此波長的光最敏感)所需要的光輻射功率為P(555)，則定義v(λ)=P(555) /P(λ)為波長λ的視見函數(見圖3)。

取400～700 nm的可見光范圍內的漫反射光譜曲線乘以視覺函數所對應明視覺相應范圍內的值，得到各樣品的相對明度值，如表1所示。

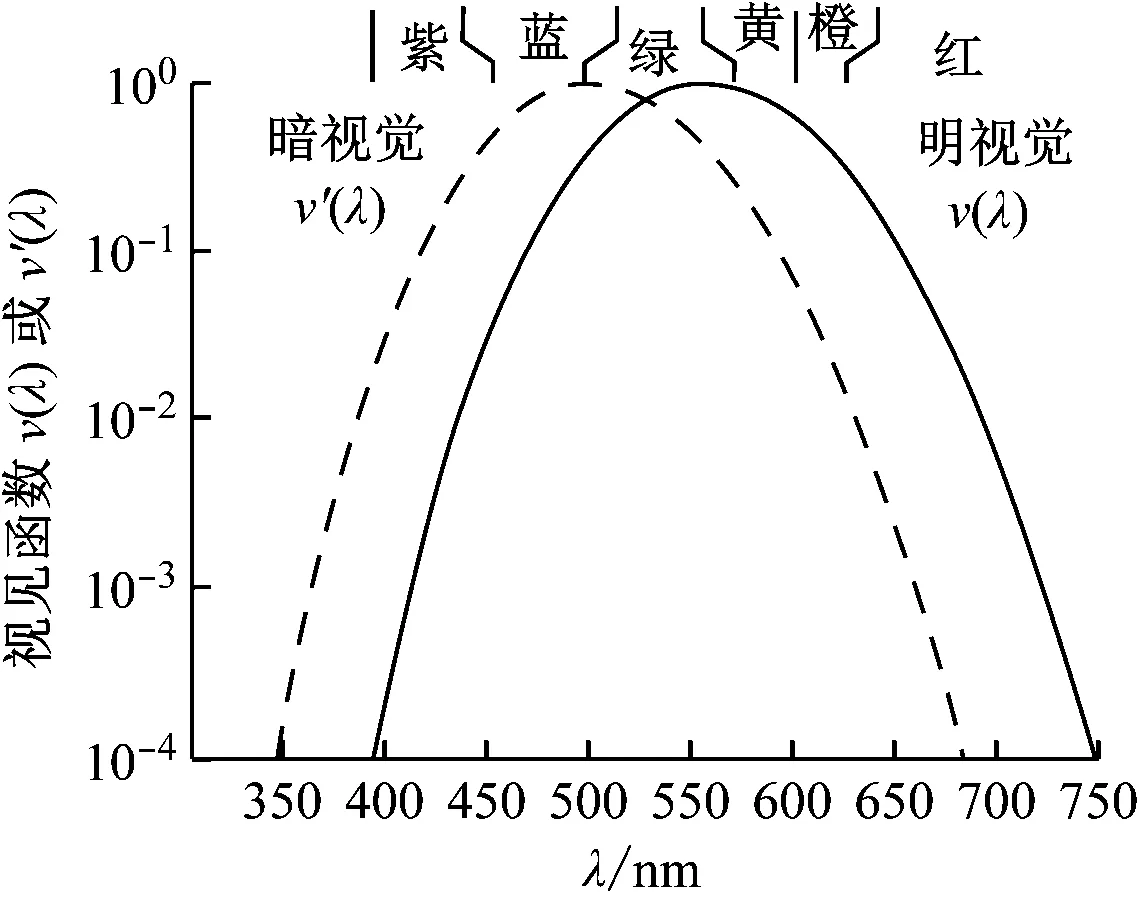
圖3 視見函數

同時，選取其中一組樣本 (Fe2O3) 通過粒度分析儀測量顆粒的平均直徑，得到如下結果：0 h(2 509 nm)、2 h(3 531 nm)、4 h(4 456 nm)、6 h(2 459 nm)；其中顆粒的平均直徑呈現上下波動是由于團聚現象的產生。粒徑在0.1～10 μm的粉末稱為微粉體，粉體顆粒間存在凝聚力(附著力)，包括范德華力、靜電吸引力等，當顆粒尺寸變小時，顆粒的比表面積增大，表面能增加，使其成為不穩定的熱力學體系，在凝聚力的作用下，顆粒自發團聚，以降低體系的吉布斯自由能[16]。通過對氧化鐵樣品計算出的相對明度值與粒徑進行比較得出：粒徑越大，明度也就越高，顏色也就越亮；粒徑越小，明度也就越低，顏色也就越暗。同時由漫反射光譜數據得到的紅色Fe2O3粉末的CIE色度圖如圖4所示。由圖4可見，研磨前后的Fe2O3粉末的色調和飽和度均未發生改變，其他粉末的色度圖也呈現出同樣的結果。

(a) 0 h (b) 2 h (c) 4 h (d) 6 h

4 理論分析

4.1 定性理論分析

假設粉末顆粒呈球形，粉末平均直徑為d，入射光波長為λ，記無量綱粒徑參量

α≡πd/λ

(1)

對于紅色Fe2O3粉末最小粒徑可算得α≈13，適用于Mie散射模型[17]：當α≤1時，Mie散射可近似為瑞利散射;α≥1，Mie散射可近似為夫瑯禾費衍射;α→∞，Mie散射可近似為幾何光學理論。當入射光是自然光且光強I0時，散射光強為

(2)

式中：r是從球心到該點的距離；i1(θ)、i2(θ)是無量綱的散射光強度函數，與θ、α有關。由上述理論可知：

由計算機模擬可知[18]，當其他變量一定時，α越大，球形顆粒的散射光強越強。對于顆粒群的多體散射，不同顆粒的散射光強非相干疊加，得到的總散射光強也應與α呈正相關。

4.2 計算機模擬

利用MiePlot軟件選取模擬參數如下：入射光波長λ=589 nm,入射光強I0=1 W/m2,Fe2O3對于589 nm光的折射率n=3.01,環境折射率n0=1,散射角度θ=180°,觀測點距球心距離r=1 m，顆粒直徑變化范圍d=2.4～4.5 μm(步長0.002)。

顆粒群數量和形態分布：球形顆粒50個，滿足對數正態分布[19]，直徑標準差為粒徑的20%。得到結果如圖5所示。由圖可見，散射光強大致與平均粒徑呈正相關，只是有所波動罷了。

圖5 計算機模擬結果

但實際情況，入射光通常為自然光，所以做了自然光條件下的模擬。在模擬參數中，入射光選太陽光譜，直徑取4個值，都為粒度分析儀測得的粒徑平均值，其他參數保持不變模擬圖如圖6所示。

(a)d=2.459 μm

(b)d=3.509 μm

(c)d=3.531 μm

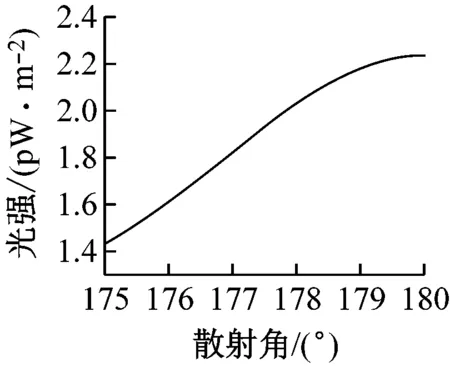
(d)d=4.456 μm

圖6 模擬圖

圖7為模擬的180°散射光強與之前實驗算得的相對明度相比較。可以看出，兩者變化趨勢一致，隨著粒徑增大，相對光強和明度都增大；這說明計算機模擬結果和我們的實驗、理論分析相符。

圖7 180°散射光強模擬與實驗對比

實際情況下，粉末顆粒為非球形，可利用橢圓截面處理任意形體顆粒群的重散射問題。通常情況下，非球形顆粒偏離球形程度越大，散射光的角分布越平坦，明暗分布也就越不明顯；但是對總散射光強的影響較小[20]。在紫外可見漫反射光譜測量中其散射光強只與顆粒直徑的呈正相關。由此可知，粉末粒徑越大，漫反射進入人眼的光強越大，人感受到的顏色的明度越高。

對于等光強單色光入射，Mie散射不會改變其光的頻率，只是不同波長光的散射強度可能會不同。我們知道，云呈現白色是因為Mie散射，散射光色調與飽和度基本與入射自然光相同。因此可以認為，Mie散射基本不會改變粉末的色調和飽和度。為證實此推測，又做了計算機模擬:圖8、9是小粒徑d=2.509 μm和大粒徑d=4.456 μm的結果圖；入射光強一定時，對于不同波長，其散射光強呈周期性波動，但由于顆粒形狀不規則，波動范圍會變小；同時，波動范圍相比于物質對光的選擇性吸收強度，可以忽略不計。

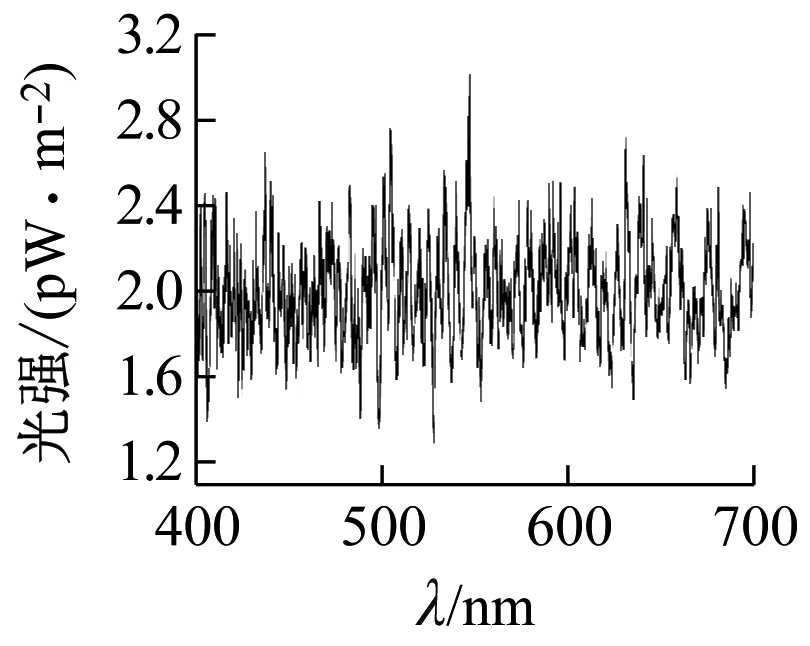
圖8 小粒徑模擬結果

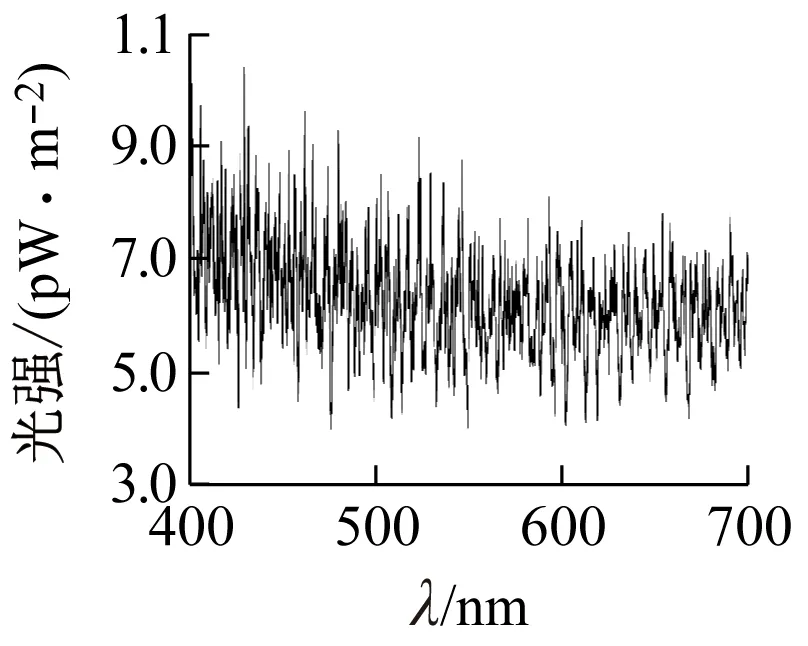
圖9 大粒徑模擬結果

5 結 語

本文制備并研究了級別的非金屬粉末，通過研究，得出以下結論：研磨程度確實會影響粉末的顏色，研磨通過改變粉末的顆粒直徑或物相來改變粉末的顏色。 粉末顏色的改變與顆粒的直徑直接相關：粒徑越大，明度越高，顏色越亮；粒徑越小，明度越低，顏色越暗。粒徑對色調、飽和度的影響很小。