基于遺傳算法的航班—登機口分配優化

董潔霜，趙 炎，劉魏巍 DONG Jieshuang,ZHAO Yan,LIU Weiwei

（上海理工大學 管理學院，上海 200093）

(Management School,University of Shanghai for Science&Technology,Shanghai 200093,China)

0 引言

隨著航空事業的發展，機場在滿足旅客快速增長的同時，航班—登機口的合理分配，旅客中轉效率和機場運作效率的提高，對大型機場而言，顯得非常重要[1]。關于登機口分配優化研究中，主要有三類研究方法：數學規劃方法、人工智能方法和系統仿真方法[2]。Gon?alves等[3]學者提出中轉時間最短的0-1整數規劃模型。L.Soi-Hoi等[4]學者建立了一個基于停機位時刻分配的專家系統。國內學者張學明[5]首次提出基于知識庫和三級推理機模式的機位自動分配系統。李耐毅、鄭志武等[6-7]學者利用仿真軟件對登機口分配情況進行模擬研究。陸迅[8]通過仿真建模對機場旅客進行了研究。本文考慮機場的航班時間安排，航班類型、登機口的類型和數量，旅客的流程時間，以0-1整數規劃為理論基礎，建立雙目標優化模型，選用遺傳算法，運用MATLAB編程求解，得到航班—登機口最優分配方案。

1 問題描述

某機場航站樓T具有出發、到達、出入境和候機功能，衛星廳S可以候機，但沒有出入境功能。航站樓T有28個登機口，衛星廳S有41個登機口，兩者之間一次單程時間只需要8分鐘，旅客無需等待。中轉流程是指中轉旅客從乘坐前一航班到達至后一航班出發時間的過程，一共有國內（D）和國際（I）、航站樓（T）和衛星廳（S）組合成16種不同的場景。每個登機口的國內/國際、到達/出發、寬體機/窄體機屬性，飛機有寬體機和窄體機兩種。

2 目標函數

2.1 模型的假設

登機口與航班必須符合一對一的分配原則，且被分配的航班類型與所使用的登機口屬性相匹配，即國際航班只能使用國際登機口，且其間航班不能挪至別處；假設每架航班到達和出發的登機口必須是同一個登機口；只有在沒有符合要求的固定登機口的情況下，飛機才會被分配到臨時機位，且臨時機位的數量沒有限制。

2.2 基于旅客中轉流程時間最少的雙目標優化模型

要使機場運營效率最高，需要將有限的登機口合理地分配給較多數量的航班，即使用最少的登機口，保證停靠在臨時機位的飛機數量最少。引入決策變量xij，當航班可以停靠于登機口j時，xij值為1，否則為0，且滿足以保證每個到達航班使用登機口是唯一的，其中，i=1,2,…,n，j=1,2,…,7。建立登機口最優目標函數：

式中：k為第j類第k個登機口，xi8為第i架飛機停靠在臨時機位，M為懲罰因子。設nih為從航班i到航班h的旅客數目；為搭乘航班h離開的所有旅客的數目；ckk'為中轉旅客從登機口k到登機口k'所用的時間。設yijk表示第i架飛機停在第j類第k個登機口，當該飛機可以停靠時，yijk值為1，否則值為0。建立關于旅客中轉總體流程時間Z2最少的目標函數[7,3]：

其中：

3 遺傳算法設計

遺傳算法對大規模復雜問題的求解有良好的表現，可以快速收斂[9-10]。本模型的求解，雖然變量過多可能會對求解造成影響，但是經過對目標函數求解的改進，可使模型較快的收斂。算法流程如圖1所示：

圖1 算法流程圖

算法對基因的編碼進行了改變，將其設置為1到8的隨機整數，并通過調整φi的大小，可以確定登機口的具體位置，如圖2所示。

4 算例分析

4.1 算例數據

中轉旅客中轉的最短時間數據如表1所示：

4.2 算例結果

通過遺傳算法不斷迭代求解得到航班—登機口最優方案。其中，31.93%的中轉旅客可以在30分鐘內完成中轉，所有的旅客都可以在一個小時內完成航班換乘。此時，在290架飛機中，共213架飛機可以分配至52個登機口機位上，其中航站樓T使用28個登機口，衛星廳S使用24個登機口，剩余的77架飛機被安排停靠到臨時機場。具體如圖3、圖4和表2所示：

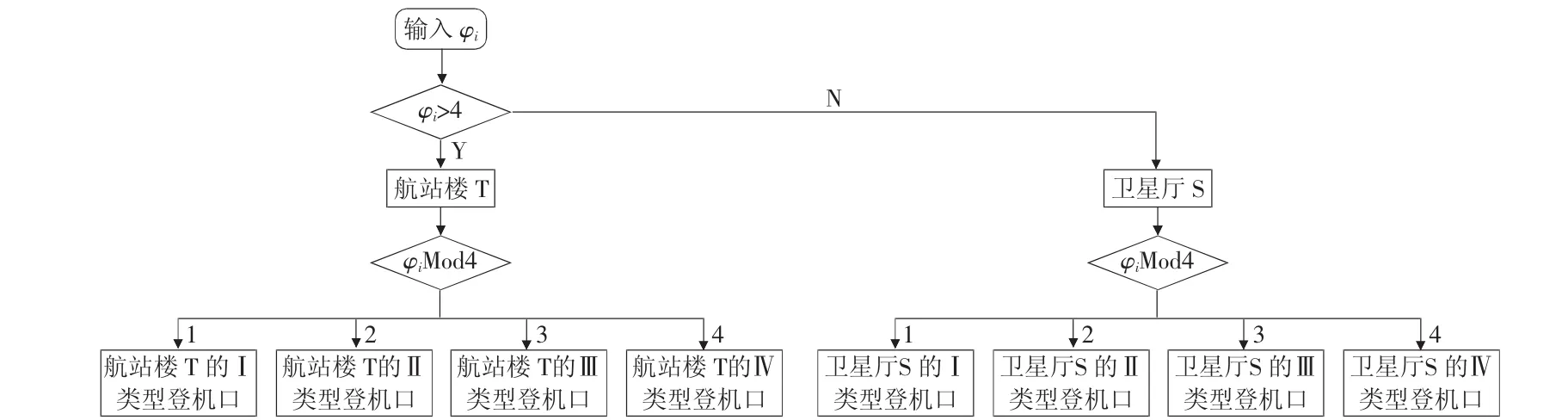
圖2 登機口位置劃分圖

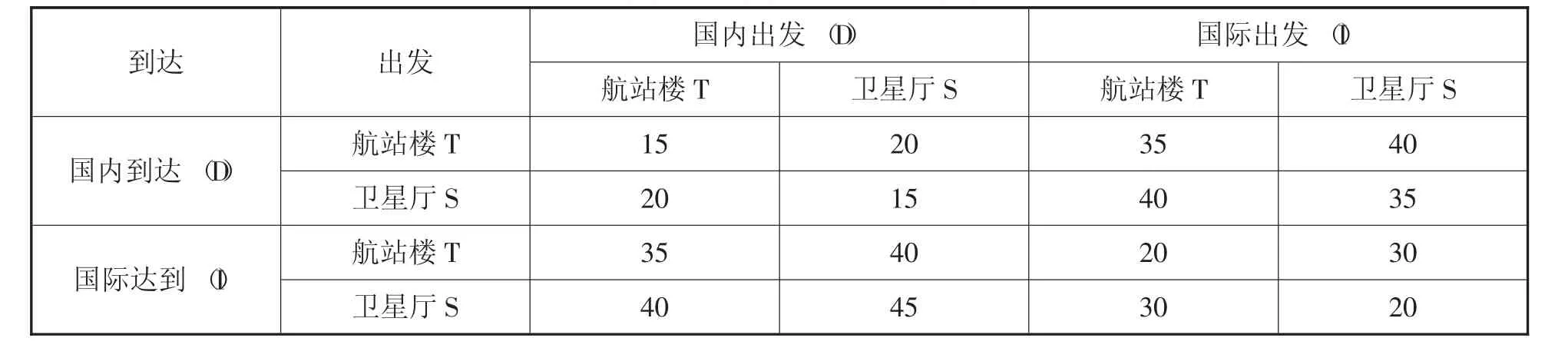
表1 中轉旅客中轉的最短時間數據表

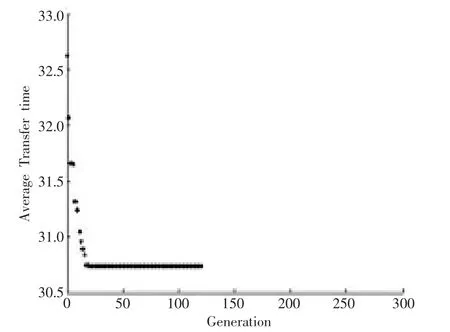
圖3 算法迭代圖

圖4 中轉旅客換乘時間比率

5 結束語

本文針對機場航班—登機口分配問題，考慮航班時間計劃、登機口類型和數量、航班類型、中轉旅客的流程時間，建立了雙目標優化模型，并利用MATLAB軟件對模型進行了求解。通過對算例的分析，驗證了模型的可行性，其研究成果可為機場管理部門提供參考。

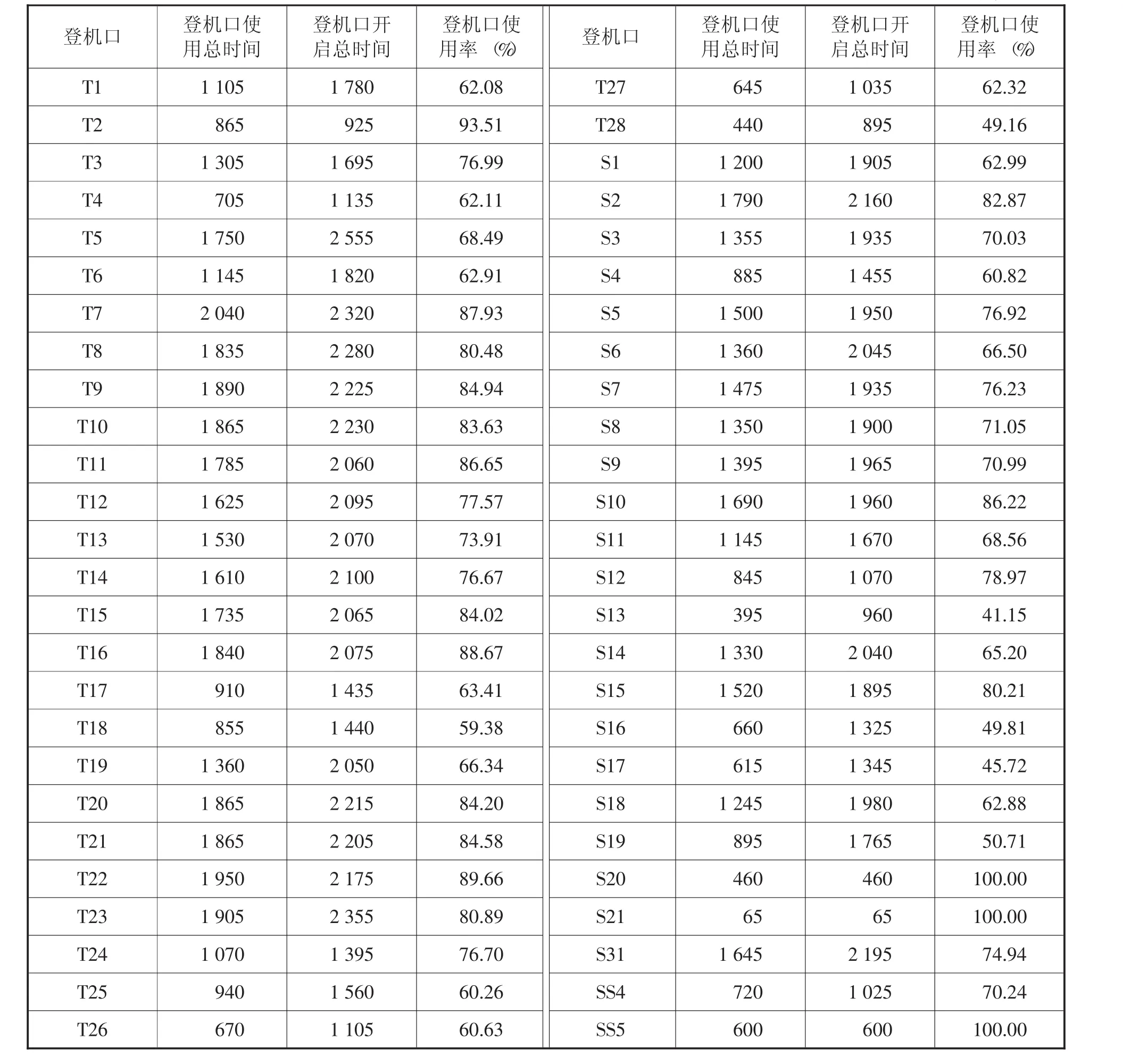
表2 登機口分配使用情況明細表 單位：min