松散破碎巖石中氣體滲流影響因素實驗研究*

馬 恒，王曉琪，齊消寒，艾純明

(1.遼寧工程技術大學 安全科學與工程學院，遼寧 阜新，123000； 2.遼寧省煤礦安全重點實驗室，遼寧 阜新，123000)

0 引言

研究松散破碎煤巖的滲流性對防治瓦斯以及煤的自燃具有重要的實際意義。國內外學者對空氣在多孔介質滲流已經有了豐富的研究。Darcy于1856年在實驗的基礎上提出了Darcy定律[1]。我國周世寧院士創造性地將描述多孔介質線性滲流特征的Darcy定律引入到煤層瓦斯流動中[2]。由于達西定律多適用于多孔介質中的低速粘性流，當流速高于某一臨界值時，Darcy定律不再滿足，呈現出non-Darcy現象。

煤是特殊的多孔介質，其復雜的孔裂隙系統使得瓦斯在煤體內的滲流往往遵循某種非Darcy滲流規律[3-4]。基于Fick擴散定律，周市偉等[5]根據煤體的異樣結構、變質程度、大小不同粒徑，探索了煤粒瓦斯擴散的影響程度；宋金星[6]通過實驗室煤樣地質強度因子的觀測、啟動壓力梯度和滲透率測試方法，初步建立了啟動壓力梯度法和地質強度因子法用于判識瓦斯運移產出流態。

張志剛[7]采用實驗研究的方法，闡述了吸附作用對煤巖非線性滲流特性的影響機制；李志強等[8]研究了溫度對瓦斯在煤粒中擴散的影響；郭紅玉等[9]運用測試啟動壓力梯度裝置，證明了煤層氣運移流態為非線性滲流；張先敏等[10]通過建立低滲透煤層氣流動數學模型，探索了低滲透煤體中氣體非線性流動的規律。

陳長華，郭嗣琮等[11-12]對非均勻孔隙介質中氣體穩定滲流進行了研究,此項研究為煤自燃提供了分析手段；聶百勝等[13]依據氣體在多孔介質中的擴散模式，分析了瓦斯氣體在煤孔隙中的擴散機理。胡國忠等[14-17]對低滲透煤的瓦斯滲流規律進行了深入的研究。

現如今，多孔介質滲流理論研究大多采用建立模型，運用實驗獲得數據進行擬合，從而得到非達西滲流運動方程。其產生機理各個學者都有不同的意見，對于非線性滲流的模型學者們還是較多青睞于冪定律。因此對于非線性的達西定律基礎上的瓦斯流動理論的深入研究是當下探索的重點方向。

經過查閱相關文獻發現，在這些實驗研究中對松散破碎巖石研究較少，在研究松散破碎巖石滲流規律過程中，設計的相關實驗并沒有同時考慮巖石的粒徑大小、巖粒空間分布以及空氣在介質中的滲流速度對氣體滲流的影響。本文通過設計松散破碎巖石的氣體滲流實驗，進一步研究了破碎巖體滲透率的變化規律，而且也豐富了破碎巖石中氣體滲流的實驗方法。

1 滲流數學模型

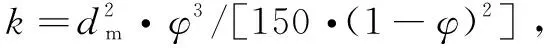
(1)

式中：v為滲流速度；k為滲透率，m2；ψ為運動粘性系數，風流取14.810-6；dm為顆粒的平均調和粒徑，m；φ為孔隙率。

空氣在多孔介質中流動，其雷諾數與孔隙率、滲流速度呈正相關關系。判定多孔介質滲流流體的速度表達式可表示為：

(2)

將研究多孔介質視為定常、不可壓縮、無源滲流流動，且為等溫過程，將非線性滲流公式在直角坐標系中展開，即可得到其氣體質量守恒定律表達式：

(3)

式中：p為滲流壓力，m2；β為顆粒形狀系數，取值為1.5；g為重力加速度，9.81 m·s-2。

在考慮粘性損失和慣性損失后，采空區滲流的動量守恒定律可表示為：

(4)

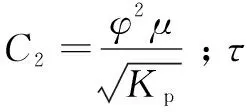
2 實驗裝置及材料

實驗滲流測試系統如圖1所示。該系統由供氣裝置、滲流裝置、流量測量裝置及壓力測試裝置組成。主體滲流裝置主要是測試長度L=1 000 mm，半徑R=95 mm的透明圓管，如圖2所示。考慮到兩端由于進風時風流不穩定影響所測的壓力數據，所以在測試管的兩端分別加上L=300 mm，R=95 mm的過渡段，使得測試的數據更加穩定、準確。在測試裝置中添加所需測量的多孔介質，填充的兩端使用填充介質粒徑相適應的篩孔網固定。將兩端的氣流穩定管體(過渡段)與測試端用法蘭緊密連接。供氣裝置為12.5 L/8 MPa微型真空泵。空氣通過連接裝置器流入到測試管中。此時，在兩端的過渡段放置皮托管，目的是通過連接微壓計來測試空氣通過多孔介質的壓差。在測試系統的端部設計一個浮子流量計，目的是用于測定管內通過的流量。微壓計最大量程為4 000 Pa。浮子流量計的最大量程2.5 m3/h。相似模擬實驗材料包括12種不同粒徑(d=4，5，6，7，8，10，12，16，20，25，28，35 mm)的玻璃球體，如圖3所示。包括5種不同粒徑(d=6，8，10，12，25 mm)的碎石子(碎石子的粒徑是通過篩網確定的)，如圖4所示。

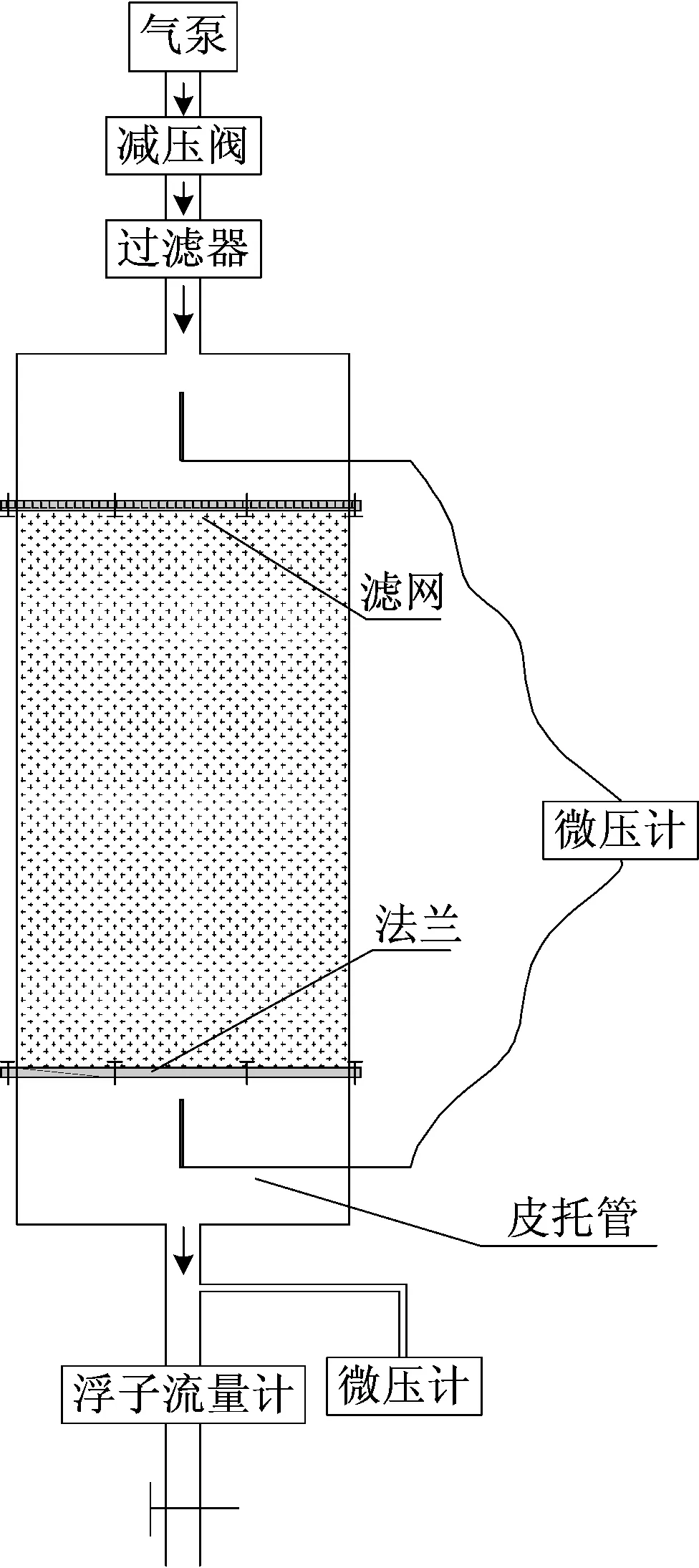
圖1 相似模擬實驗滲流測試系統Fig.1 Seepage test system with similar simulation experiment

圖2 多孔介質填充段Fig.2 Filling section with porous media

3 實驗過程

為了使實驗更具有目的性，使測得數據更科學，更準確，對實驗條件進行如下簡化。假設滲流相似實驗符合以下條件：

1)空氣為不可壓縮流體。

2)破碎的煤或巖體自身無氣體釋放。

3)不考慮介質所受的力。

4)滲流過程為等溫過程。

實驗裝置如圖2所示。依據實驗填充多孔介質粒徑的不同，在測試系統管的兩端安裝符合要求的濾網；在填充的時候，使用震動實驗裝置使其能夠緊密填充；根據填充前后的質量，求出填充多孔介質的質量。固定好滲流裝置的兩端，保證其良好的氣密性；將裝有填充介質的滲流裝置連接到其他部件，打開微型真空泵，通過手動調節按鈕控制不同的流量，在壓差計示數達到穩定狀態后，讀取讀數即可；記錄完每組實驗流量以及壓差計讀數后更換不同粒徑的介質重復上述的實驗步驟。

圖3 不同粒徑的測試玻璃球(從左到右粒徑大小分別為35，28，25，20，16，12，10，8，7，6，5，4 mm)Fig.3 Tested glass spheres with different particle sizes (Particle size from left to right was 35,28,25,20,16,12,10,8,7,6,5 and 4 mm respectively)

圖4 不同粒徑的測試碎石子(從左到右粒徑大小分別為6，8，10，12，25 mm)Fig.4 Tested gravel with different particle sizes(Particle size from left to right was 6，8，10，12，25 mm respectively)

在進行采空區滲流實驗過程中，先對12種單一的粒徑玻璃球構成的堆積介質進行均質各向同性的實驗研究；然后對單一粒徑的碎石子進行非均質的實驗研究。在單一粒徑構成多孔介質的實驗基礎上，再將6，12，25 mm粒徑的玻璃球按照不同體積比進行混合，將相似粒徑的碎石子6，12，25 mm按照不同比例進行混合；最終分析單一粒徑球體(均質)、石子(非均質)、混合粒徑玻璃球體、混合粒徑碎石子滲流規律，以及不同介質、填充的粒徑大小、填充多孔介質孔隙率對氣體滲流的影響。

3.1 粒徑和孔隙率的關系分析

實驗中將12種單一粒徑的玻璃球體依次填充在滲流測試的實驗裝置內，使其緊密填充。稱量分別得到平均質量M、每組填充前的質量以及填充完的總質量，算出每組粒徑玻璃球體的填充質量并進行記錄。再分別測量出每一種單一粒徑的球體質量m，因為玻璃球體的體積可知，可以求出每種粒徑填充的玻璃球體所占的總體積V球。因為滲流實驗裝置模型的總體積V可知，所以可以算出孔隙的體積V孔，求出每種粒徑填充時的孔隙率P，如式1。測量數據見表1。

(5)

基于表1數據，繪制了不同粒徑—孔隙率之間的關系圖，如圖5所示。

圖5 不同粒徑小球和孔隙率關系Fig.5 Relationship between different particle sizes and porosities

根據粒徑和孔隙率的散點圖通過擬合，得到擬合公式為y=0.004 8x+0.233 3；其中各種測試粒徑玻璃球體的粒徑大小與孔隙率的相關系數在0.98以上，說明兩者具有很好的相關性。從圖5可以看出，粒徑與孔隙率呈正相關關系。

3.2 粒徑、滲透速度對滲透壓力的影響

測試由12種粒徑不同的玻璃球體單獨構成的自由堆積多孔介質，其流量與壓力梯度數值。流量的測試范圍從0.1～1 m3/h，測試出了10組數據。實驗測得流量將其轉換成比流量(滲流速度)，測得的壓力差值轉換成壓力梯度。將12種單一粒徑的玻璃球體滲流速度和對應的壓力梯度繪制成散點圖，如圖6所示。

圖6 單一粒徑的玻璃球體滲流速度與對應的壓力梯度散點圖Fig.6 Scatter plot graph of seepage velocity of glass sphere with single particle size and corresponding pressure gradient

根據圖6分析得到，12種單一粒徑的玻璃球體作為堆積介質構成的多孔介質空間，滲流速度與壓力梯度呈現正相關關系。其中粒徑為d=4，5，6，7，8，10，12 mm的小玻璃球體的滲流速度與壓力梯度的變化趨勢基本為線性，滲流符合Darcy定律。根據達西定律，擬合直線的斜率可表示實驗填充多孔介質的滲透率，對于同一種流體而言介質的滲透率應該為定值。

當粒徑為d=16，20，25，28，35 mm時，滲流狀態滲流速度開始出現明顯的非線性滲流，由實驗可以得出，滲流的起始階段都比較符合線性滲流定律。隨著粒徑的逐漸增大，滲流狀態由線性滲流轉變為非線性滲流狀態，其滲流速度的值也在不斷地減小。很明顯，空氣在大粒徑組成的多孔介質中的滲流系數不是一個常數。

3.3.2推進農村生活垃圾治理 指導長江經濟帶11個省(市)按照“標本兼治、綜合施策、突出重點、分類施策”要求，做好非正規垃圾堆放點排查和整治工作。建立農村生活垃圾集運處置體系，鼓勵具備條件的地方實行村收集、鎮轉運、縣處理。有條件的地區要推行適合農村特點的垃圾就地分類和資源化利用方式。發揮好村級組織作用，增強村集體組織動員能力，支持社會化服務組織提供垃圾收集轉運等服務。

4 非均質各向同性多孔介質滲流實驗

上述實驗分析是以單一粒徑的玻璃球作為填充物，其多孔介質是均質各向同性的，但實際松散破碎巖石是非均質各向異性的。為使相似模擬實驗更加準確，故采取更加貼近實際的碎石子作為填充物進行實驗分析，形成非均質實驗條件。

4.1 粒徑和滲透速度對滲透壓力影響分析

對5種粒徑(粒徑為d=6，8，10，12，25 mm)的碎石子，單獨構成的自由堆積體非均質各向多孔介質進行滲流測試實驗。

流量的測試范圍0.1～1 m3/h。測試出了10組數據。根據實驗得到了在不同流量下的壓差變化值。基于得到的數據值，將不同滲流速度與相對應的壓力梯度繪制成散點數據圖，如圖7所示。

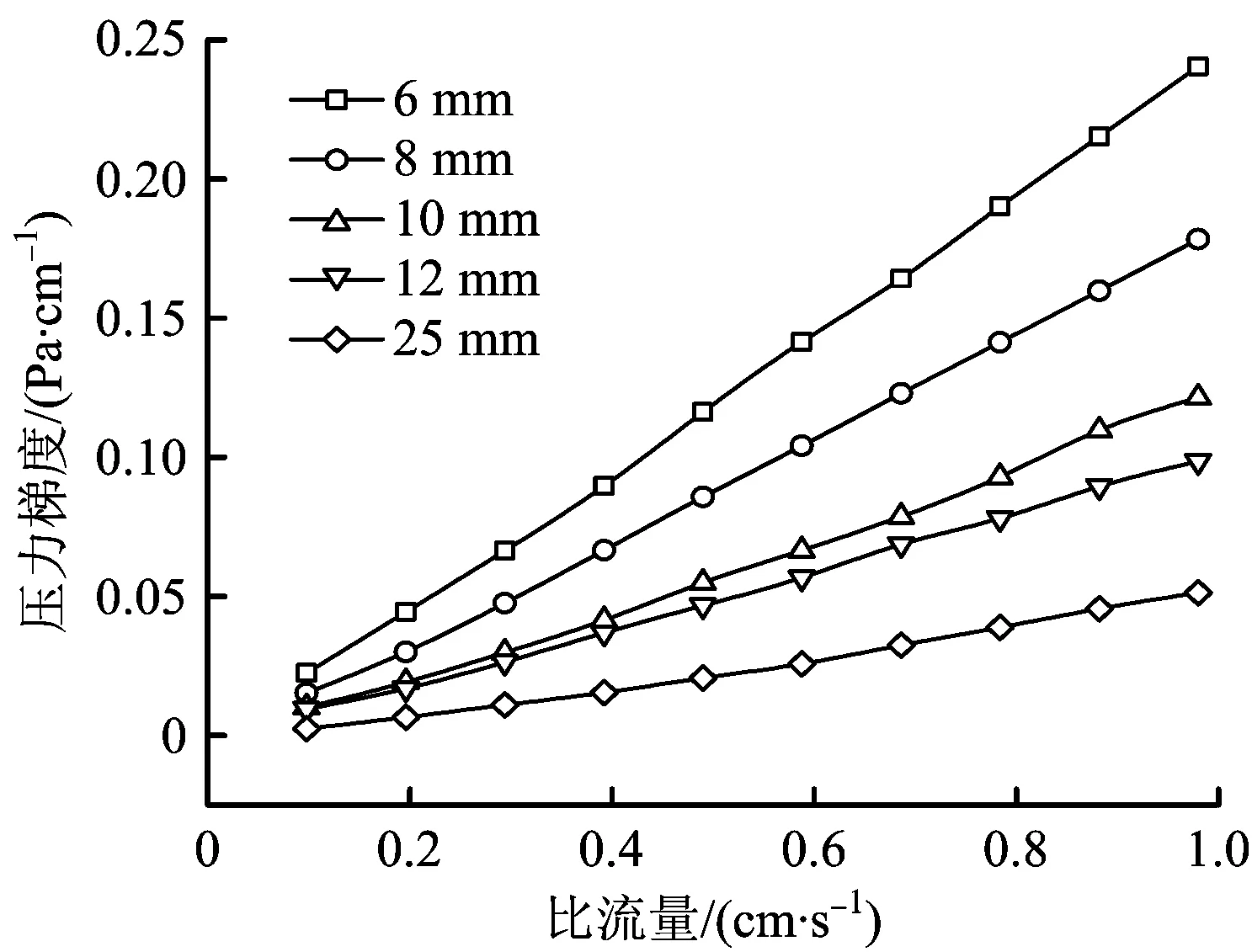
圖7 不同粒徑的碎石子滲流速度與壓力梯度Fig.7 Seepage velocity and pressure gradient of gravel with different particle sizes

從圖7中可以看出，以單一粒徑的碎石子作為堆積介質構成多孔介質空間，隨著滲流速度的增加壓力梯度也在不斷地增加。滲流剛剛進行的時候，滲流的規律符合Darcy定律。隨著空氣滲流速度的增大，其滲流狀態由線性向非線性滲流轉變。測試結果表示：隨著填充介質粒徑的逐漸加大，滲流狀態也由線性向非線性滲流轉變。

通過前面對玻璃球體進行實驗得到的滲流速度和壓力梯度的數據和擬合曲線，與碎石子的數據作比較。分析研究相同粒徑的玻璃球體和碎石子，不同滲流速度下對應的壓力梯度，如圖8所示。

由圖8可以看出，相同粒徑下，在粒徑較小時的碎石子和小球變化規律不一致，因為碎石子的形狀不規則，填充受到多種因素的影響。但粒徑較大時不論均質還是非均質其變化規律基本一致。

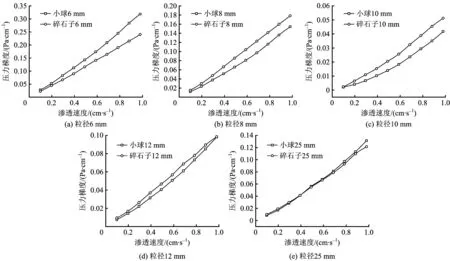
圖8 相同粒徑下的碎石子和小球滲流速度與壓力梯度Fig.8 Seepage velocity and pressure gradient of gravel and ball with same particle size

5 原煤倉縱深方向多孔介質滲流實驗

5.1 不同粒徑球體填充滲流實驗

圖9 混合小球充填示意Fig.9 Schematic diagram of mixed ball filling

圖10 混合碎石子充填示意Fig.10 Schematic diagram of mixed gravel filling

由圖11看出，均質小球隨著速度的增加，滲透的壓力梯度都在逐漸增高。其中圖11(a)壓力梯度隨著滲透速度變化更為明顯，即由于小粒徑玻璃球體所占比例發生變化，引起壓力梯度變化更為明顯，小粒徑所占比例越高，壓力梯度變化越大。圖11(b)壓力梯度隨滲透速度變化較小，雖然大粒徑占值比例越來越大，但是壓力梯度增加并不明顯，特別是大粒徑占40%和50%的2條曲線近乎重合，幾乎沒有變化。圖11(a)和圖12(a)滲透速度與壓力梯度均呈現非線性變化規律，說明在測試方向上，當孔隙率發生變化時，無論粒徑多大，滲流都不再符合線性規律，而是呈現非線性規律。

表2 10組實驗6,12,25 mm時各占的體積比Table 2 Volume ratio of ten group of 6,12 and 25 mm respectively %

圖11 “均質”小球滲流速度與壓力梯度Fig.11 Seepage velocity and pressure gradient of “homogeneous” ball

圖12 “非均質”碎石子滲流速度與壓力梯度Fig.12 Seepage velocity and pressure gradient of “heterogeneous” gravel

從圖11與圖12進行對比可以看出，不同比例玻璃球體和碎石子填充構成的多孔介質滲流的規律基本相同。

6 結論

1)粒徑大小和滲透速度與滲透壓力梯度呈現正相關關系；在保證相同的滲流速度情況下，孔隙率是影響壓力梯度變化速率的主要因素。

2)隨著粒徑增大，滲流狀態由線性滲流轉變為非線性滲流的滲流速度的值在不斷減小。

3)小粒徑所占比例發生變化，引起壓力梯度變化更加明顯，小粒徑所占比例越高，壓力梯度變化越大。

4)滲透速度與壓力梯度均呈現非線性變化規律，說明在測試方向上，當孔隙率發生變化時，無論粒徑多大，滲流都不再符合線性規律，而是呈現非線性規律。