基于改進PPC模型的鐵路棄渣場綜合風險評價系統*

吳偉東，茍唐巧，許博浩，潘海澤，何 鑫

(西南石油大學 土木工程與建筑學院，四川 成都 610500)

0 引言

棄渣場是鐵路工程項目的重要組成部分，一般作為滿足鐵路工程建設的取土與棄土需求而存在，目前我國大型棄渣場約有幾萬座，其中大多數地理位置處在山嶺坡地，部分處在峽谷，而棄渣場屬于人造邊坡，在各種內外誘因下，發生滑坡泥石流等風險災害的可能性較大，如，2015年深圳光明新區發生棄渣場滑坡事故共造成33 棟建筑物被掩埋或不同程度損壞，73人遇難[1]，所以棄渣場的綜合風險評價具有迫切的現實意義。

隨著我國鐵路工程技術的發展與突破，山區鐵路的規模及其占全國鐵路的比重都在逐年上升，由此產生的大量棄渣場不僅破壞了沿線生態環境也提高了自然災害的發生率，于是學術界開始重視棄渣場的相關研究，這個階段的研究方向主要有2個分支：一是試圖找到影響棄渣場水土流失和土壤侵蝕的主要因素，王大為等[2]發現棄渣場土壤流失受降雨量和降雨時間乘積、植被類型和表層土前期土壤含水量的影響；二是探索科學有效的植被恢復方法，穆軍等[3]對干熱河谷棄渣場土壤采用了“保水劑+保水緩釋肥”處理方法，發現植被恢復效果較好。而目前國內外學者關注的熱點則是轉向了棄渣場的穩定性評估和選址研究，周昌群[4]通過分析棄渣場不同堆載形式、不同堆置步驟下變形演變規律，優化設計方案，提高其穩定性。袁普金等[5]提出了歷史發生頻率法和模型預測選址法的棄渣場安全選址方法。從以上研究中發現目前對棄渣場的研究分支眾多，但是缺乏對棄渣場綜合風險評價的研究，大量專家學者從某一個或幾個方面來研究棄渣場的安全顯然缺乏整體性和系統性，不能為棄渣場潛在和已發生的風險問題提供較為有力的決策支持。

鑒于此，本文擬將投影尋蹤聚類模型引入棄渣場綜合風險評價領域，考慮多個維度的本質特點，建立較為系統和全面的風險評價體系，以期從更深更廣的研究視角來解決棄渣場綜合風險問題。

1 評價標準和指標體系的建立

目前國內外對于棄渣場綜合風險評價的研究較少，指標體系的建立并沒有一個權威的參考，所以在遵循系統性、針對性、綜合性的原則上，查閱相關文獻并參考《鐵路路基設計規范》《鐵路建設工程安全風險管理暫行辦法》等行業規范。從“棄渣場邊坡條件”、“棄渣場物料性質”、“氣象條件”、“地形與地基條件”、“棄渣場基本情況”、“支擋結構情況”6個維度建立了共19個因素的指標體系，如圖1所示，其中“內摩擦角”、“黏聚力”、“走向夾角”、“擋渣墻實際高度”4個指標為負向指標，其余指標為正向指標。同時將風險等級分為“Ⅰ級(輕微風險)”、“Ⅱ級(低度風險)”、“Ⅲ級(中度風險)”、“Ⅳ級(高度風險)”4個等級，定量指標各等級的值域和定性指標各等級的定義都有明確的規定，見表1。對于Ⅰ級到Ⅳ級4個風險等級的接受準則分別為“可忽略”、“可接受”、“不期望”、“不可接受”，由于前2個等級風險較低，可不采取風險應對措施，而Ⅲ級則要采取相應措施使其風險降低到可接受的范圍內，Ⅳ級必須高度重視，并不惜一切降低其風險。

表1 棄渣場綜合風險等級評價標準Table 1 Evaluation criteria for comprehensive risk grade of abandoned dreg site

2 棄渣場綜合風險評價理論模型

2.1 風險評價模型的選擇

風險評價的方法有很多，如故障樹分析法用于工程系統安全或事故風險比較單一的分析，對于區域綜合風險評價不太適用[6]；概率風險評估法是對已發生的風險資料和實驗結果數據進行分析，評價各類風險，但其存在不確定變量多使得計算量較大等問題；蒙特卡羅法是針對有確定概率分布或大量樣本的風險事件，但只能解決已確定的風險評價和較為單純風險問題[7]。多數的統計模型不能解決定性和定量等目標較多的復雜情況。由此，本文建立改進投影尋蹤聚類風險評價模型，優化參數減少計算量，避免專家賦權的人為因素影響，更準確、全面地進行鐵路棄渣場綜合風險評價。

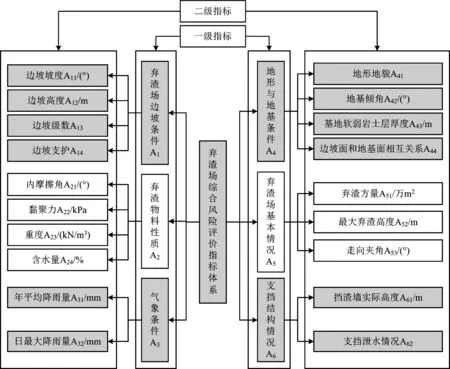
圖1 棄渣場綜合風險評價指標體系Fig.1 Index system for comprehensive risk assessment of abandoned dreg site

2.2 PPC模型

PPC模型是Friedman 和Tukey[8]基于Kruskal[9]的觀點建立的一種特征提取方法。其原理是將樣本原始高維數據從不同方向投影到低維空間，通過分析低維空間的數據結構特點，達到研究高維數據的目的。該方法能最大化遵循樣本數據的本質和特征，降低人為主觀因素對聚類結果的干擾，同時大大減少了計算量。目前PPC模型主要被應用在水資源評價[10]和土壤分析[11]等領域，并與云模型、BP神經網絡等方法相結合，以應對不同的研究環境和目標。但在土木工程領域，尤其是在棄渣場的綜合風險評價中幾乎沒有得到應用。

設各指標的樣本集{x*(i,j)|i=1,2,…,n;j=1,2,…,m}，其中x*(i,j)為第i個樣本第j個指標值；n,m分別代表樣本的數量和指標的數量，若令a=(a1,a2,…,am)為投影方向，PPC模型就是將x(i,j)投影到a上，得到一維投影值z(i):

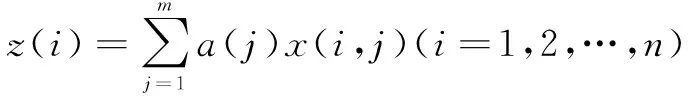
(1)

PPC模型中投影指標函數由聚類類別的局部密度和歸屬于該聚類類別的樣本之間整體距離相乘構造而成的，可以表示為：

Q(a)=SZDZ

(2)

(3)

(4)

式中：SZ為投影值z(i)的標準差；DZ為投影值z(i)的局部密度；E(z)為z(i)(i=1，2，…,n)的平均值；R為局部密度的窗寬半徑；r(i，j)(i=1，2,…,n；j=1，2,…,n)為樣本i和樣本j之間的距離；u(t)為單位階躍函數，當t≥0時，其函數值為1，當t<0時，其函數值為0[12]。根據樣本聚類對投影目標函數進行優化，當SZ和DZ同時取得最大值時，聚類效果最好[13]。所以目標函數可以表示為：

maxQ(a)=SZDZ

(5)

(6)

2.3 密度窗寬R的確定

PPC模型中局部密度的半徑R需要提前確定，目前R的選取并沒有一個公認統一的方法，但它對最終聚類結果的影響極大，取值過大會使得大量樣本被歸到同一點團內，達不到聚類的效果；取值過小，則會出現過多點團，點團內樣本較少，同樣影響聚類結果的可靠性。裴巍等[14]提出了一種基于聚類思想局部密度窗口半徑確定方法，改進了PPC模型。具體思路如下：對進行聚類的n個樣本做K均值聚類，假定將n分成k類(點團)，每個點團中含有樣本數為x1，x2，x3，…，xk，且x1+x2+x3+…+xk=n，r(i，j)表示投影點之間的距離，即r(i，j)=|z(i)-z(j)|。降序排列，記為r(i，j)(k)，k=1，2，3，…，n2，r(i，j)(k)為降序排列后序號為第k個r(i，j)值，則R=r(i，j)(p)，其中，p=∑xixj(i≤i，j≤k)。R的取值應該滿足不同點團之間的每個樣本的r(i，j)最小值應該大于R，而同一點團內的樣本的r(i，j)≤R，所以對于某一點團來說，滿足R-r(i，j)<0的樣本將不計入該類別內，具體個數為p=∑xixj(i≤k，j≤k)，所以將r(i，j)降序排列后，第p個r(i，j)的值可以作為R的合理取值，即R=r(i，j)(p)。

3 案例研究

為驗證本文建立的研究體系的可靠性與科學性，將新建鐵路貴昆線的10座代表性棄渣場樣本作為案例研究。根據所建立的指標體系，收集施工方對樣本的現場實地勘測數據，如表2所示。

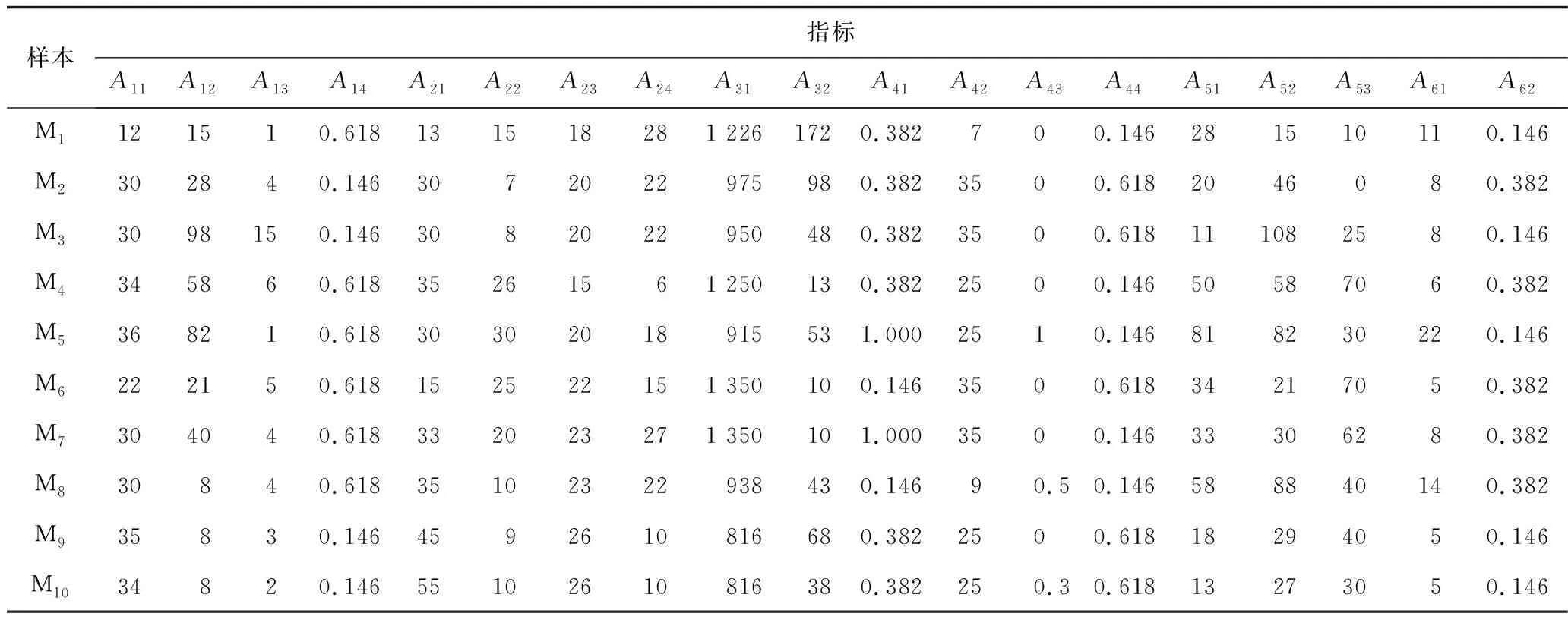
表2 棄渣場樣本原始數據Table 2 Raw data from samples of abandoned dreg site

3.1 樣本數據的無量綱化處理

由于各個指標的取值范圍不同，不能進行直接比較，所以樣本原始矩陣需要做無量綱化處理。

對于效益型指標：

(7)

對于成本型指標：

(8)

式中：xmax(j)和xmin(j)分別為第j項指標取值范圍的最大值和最小值，x(i，j)為第i個樣本第j項指標無量綱化后的值。

所建立的指標體系中，A14，A41，A44，A624項指標為定性指標，利用黃金分割法[15]將其定量化，將指標體系中定性指標從Ⅳ級到Ⅰ級4個等級的取值分別劃分為：1，0.618，0.382，0.146。

3.2 樣本數據的處理與分析

完成棄渣場樣本的數據處理之后，代入式(2)中計算最佳投影方向和投影值，根據2.2所提及的方法，初步決定將10座棄渣場樣本分為4類，每1類包含的樣本數量為x1=4，x2=4，x3=1，x4=1，則p=∑1≤i，j≤4xixj=66，所以R=r(i，j)(66)，這表示將所有樣本之間的距離r(i，j)降序排列后第66個r(i，j)即為R的取值。同時通過遺傳算法來對PPC模型進行優化，參數設定為種群規模N=400，交叉概率Pc=0.8，變異概率Pm=0.2，迭代次數200次，最佳適應度隨迭代次數的變化趨勢如圖2所示。

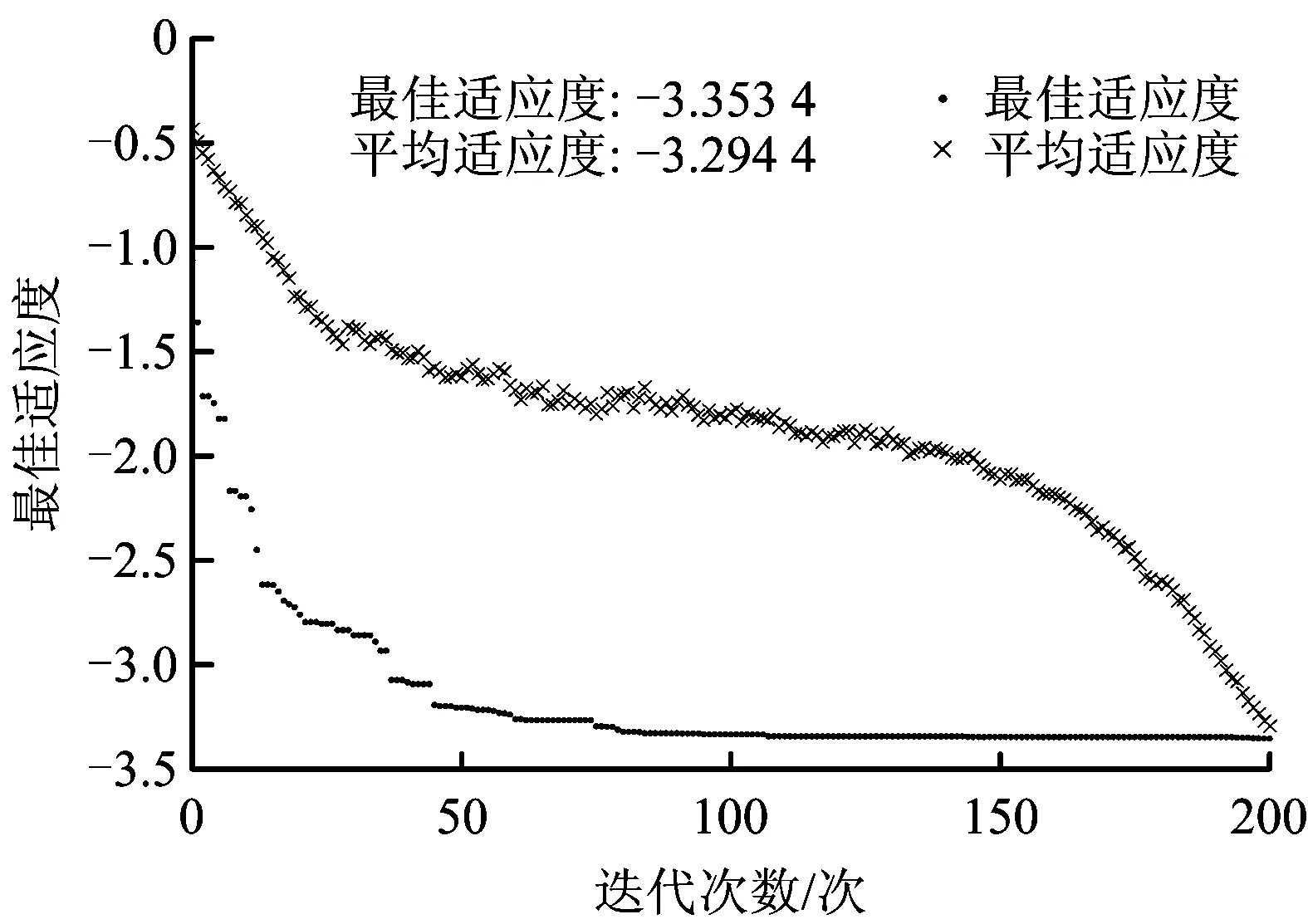
圖2 最佳適應度隨迭代次數的變化趨勢Fig.2 Change trend of optimal fitness with number of iterations

從圖2中可以看出，經過200次迭代后投影指標函數的最大值約為-3.353 4，同時得到最終的最佳投影方向a=( 0.150，0.369，0.264，0.330，0.189，0.007 63，0.024 2，0.099 2，0.183，0.016 5，0.432，0.547，0.131，0.152，0.017 8，0.100，0.090 6，0.001 38，0.191)；樣本投影值z=( 1.043，1.391，1.739，1.392，1.736，1.390，1.739，1.027，1.043，1.021)。利用樣本投影值計算結果做出樣本聚類圖如圖3所示，得出10座棄渣場樣本聚類結果為3類：c1={M1，M8，M9，M10}，c2={M2，M4，M6}，c3={M3，M5，M7}。

圖3 棄渣場樣本聚類圖Fig.3 Cluster diagram of abandoned dreg site samples

根據最佳投影方向可以對本文所建立的指標體系中的指標做重要性的橫向比較，如圖4所示。同時可以計算得到6個一級指標的權重值，分別為0.337，0.046，0.034，0.526，0.019，0.036。以此可以看出A41，A42，A12，A13，A145個指標對棄渣場綜合風險的影響較高，相應的這5個指標對應的2個一級指標A1和A4權重值之和高達0.863，而近年來被大多數專家學者作為研究棄渣場安全穩定性的主要因素“棄渣物料性質”的權重值僅為0.046，其下級指標中也只有“內摩擦角”的投影方向值稍高，但依然沒有超過0.2。

從以上數據分析中可以看出，控制棄渣場的綜合風險，安全選址的重要性和優先級是要遠高于對棄渣物料性質的分析。因為邊坡、地形和地基條件由棄渣場所處地理位置直接決定，一旦選址方案確定，都將成為不可抗力因素，無論后期對棄渣渣土類別如何控制，都對風險的降低貢獻較小，還會造成較大的經濟損失。

圖4 最佳投影方向橫向比較圖Fig.4 Horizontal comparison chart of optimal projection direction

3.3 棄渣場綜合風險評價結果

利用3.2得出的最佳投影方向，計算出評價標準中每一個風險等級的投影值，作為被評價樣本的風險等級劃分的定量標準，如表3所示。本文所列舉的10個棄渣場樣本最終的風險等級如表4所示。M3，M5，M7此3個樣本的風險等級為Ⅲ級，接收程度為“不期望”，需采取相應的風險應對措施降低其風險；而其他7個樣本風險等級為Ⅱ級，接受程度為“可接受”，風險較低，無需采取風險應對措施，做好正常的監控即可。

表3 風險等級評定標準的投影值Table 3 Projection values of risk rating criteria

表4 風險等級評價結果Table 4 Results of risk rating evaluation

為了對M3，M5，M7此3個樣本做出針對性、科學性的風險應對措施，根據每一個指標所收集到的實際數據對其進行進一步的風險分析，主要分析的重點為“棄渣場邊坡條件”和“地形與地基條件”這2個權重占比較重的指標。首先從“棄渣場邊坡條件”方面可以看出三座棄渣場都存在邊坡高度太高的問題，M3達98米，邊坡級數為15級，在如此高危的邊坡高度下，M5和M7卻僅采取簡單的植物防護措施，這顯然增加了風險。而在“地形與地基條件”方面，M3雖處在一般山嶺區，但棄渣場邊坡面與地基結構面的關系卻是順向的，而地基傾角高達35度，使得產生滑坡的可能性較大；M5和M7則處在峽谷地帶，地基傾角較高，M5所處地理位置的地基更是存在軟弱巖土，降低了其穩定安全水平。

根據以上分析本文提出以下風險應對措施：優先考慮對M3，M5，M7此3座棄渣場進行搬遷處理，因為從分析的結果來看，選址的不科學是造成3座棄渣場風險較高的直接決定性因素，建議搬遷至一般山嶺區和山間平地，同時要對地質情況進行勘測，避免選擇陡坡和地基情況較差的位置作為棄渣場搬遷位置。如果因為方案無法更改或支出超過成本預算不能對棄渣場進行整體搬遷，則只能從棄渣體的物料性質和支擋泄水措施入手以期降低其風險。

4 結論

1)借鑒K均值聚類思想的投影尋蹤模型在引入棄渣場綜合風險評價后，能夠最大化反映評估樣本最本質的數據結構和內在聯系；解決影響因素維度高，定性與定量因素交錯等難題；同時有效避免采用傳統評價方法產生的經驗主義，使評價結果更具客觀性和科學性。

2)通過對案例的研究分析發現，“棄渣場邊坡條件”和“地形與地基條件”2個維度權重值之和高達0.863，而近年來被大多數專家學者作為研究重點的“棄渣物料性質 ”的權重值僅為0.046，反映了安全選址應作為棄渣場風險控制管理的重點。

3)本文所建立的評價系統，除樣本數據需實地勘測與人工收集外，其余過程均占用資源少，耗時短，成本低，也不受樣本量大小的影響，為棄渣場綜合風險評價提供了新的研究思路。