基于區間概率優勢決策模型的滑坡治理方案優選研究*

王 飛，馬裕超，張 輝，王 丹

(1.南陽理工學院 建筑與城市規劃學院，河南 南陽 473004； 2．中國電力科學研究院有限公司 輸變電工程研究所，北京 100055)

0 引言

滑坡災害是一種高頻發性和強危害性的地質災害，會給災區人民群眾的生命財產帶來嚴重威脅[1]。科學合理的治理方案不僅可以穩定滑坡體變形和減少工程投資，還可以有效降低對環境的負面影響[2]。不同的滑坡治理方案的工程投資、施工要求、技術風險和環境影響不盡相同。因此，在治理工程項目設計初期階段，如何優選出科學合理及經濟有效的治理方案，顯得尤為重要。目前，很多學者對此進行了有益的探討：王恭先[3]指出應從滑坡體治理項目可行性、經濟效益、社會環境效益和施工技術難度等方面對其進行綜合定性評價，但此方法要求工程技術人員有較豐富的工程實踐經驗；王威等[4]基于經典綜合評價理論與蒙特卡洛隨機模擬技術，對某滑坡災害治理方案進行綜合評價和科學決策；王念秦等[5]構建了基于安全、經濟和技術等因素的滑坡綜合治理方案比選模式，并采用熵權決策方法對滑坡治理方案進行定量優選，但在決策過程中并未考慮決策指標之間的屬性關系。綜上，這些研究工作對滑坡防治工程方案的評價與優選具有重要的科學借鑒意義。

但在實際的滑坡工程治理方案優選過程中，其優化選擇往往是決策者通過分析指標屬性信息，對有限已知方案進行綜合評價與優選的過程，特別是當各決策方案指標屬性信息未確知時，呈現出顯著的復雜性、區間性、不確定性與非線性等特征[6]。因此，可將其歸納為多屬性決策方案排序問題。目前，該理論在洪水災害風險區劃[7]、礦業資源綜合開發評價[8]和電網企業投資決策優選[9]等領域得到廣泛應用，但鮮少應用和驗證于滑坡災害治理領域。鑒于此，本文在博弈決策論和粗糙集理論基礎上，借鑒概率優勢關系屬性和Minimax算法優化思路[10-11]，考慮到每個決策對象在決策過程中，都期望最大限度地減少對理想對象的偏離，通過對決策信息的集成，使每個決策對象的綜合屬性值最大化，進而按照綜合優勢概率測度值進行排序擇優。最后，通過工程實例驗證了模型在滑坡治理方案優選中的科學性和有效性。

1 區間概率優勢決策理論實現

1.1 區間可能度表征

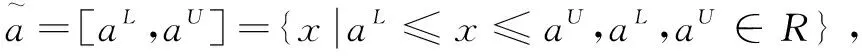
(1)

1.2 區間數序列優勢關系推論

(2)

推論1：當進行正、負理想方案決策時，則分別有：

(3)

若式(4)是正理想方案時，則有式(5)成立。

(4)

c*L≥max{aL,bL},c*U≥max{aU,bU}

(5)

推論1的證明過程表明：決策方案屬性值的概率測度與其優勢度之間存在等價關系。

(6)

推論2：當進行正、負理想方案決策時，則分別有：

(7)

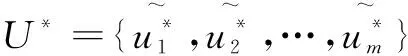
(8)

即：

(9)

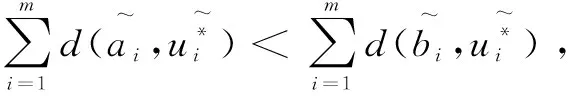
1.3 利用屬性優勢關系確定指標權重

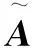
對于效益型指標與成本型指標，分別有：

(10)

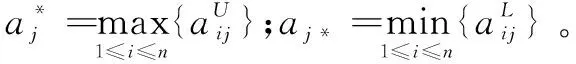
其屬性優勢關系為屬性cj?ck的概率測度，其屬性優勢關系比較如式(11)所示：

(11)

其構成的矩陣如式(12)所示：

Pm×n=p(cj?ck)m×m

(12)

其概率優勢度矩陣是屬性cj在決策過程中的綜合概率優勢度，亦可定義為其權重度量值。

(13)

1.4 模型實現步驟

2)利用式(11)～(12)計算得到概率優勢度p(cj?ck)，且形成概率優勢矩陣Pm×n，最后利用式(13)求得其權重度量值ωcj；

(14)

則決策對象的優勢度xj優于xk的概率測度如式(15)：

(15)

式(15)可表達為：

Pm×n=p(xj≥xk)m×m

(16)

4)依據公式(16)求解U={x1,x2,…,xn}的優勢概率測度值大小，并對其排序擇優。

2 工程案例計算與分析

2.1 工程背景

該滑坡位于某規劃鎮中心區上游，滑坡周邊地貌類型為黃土梁峁斜坡區與河谷階地，滑坡區地形西高東低，北高南低，總體由西向東傾斜，滑坡體上陡坎發育，呈南北向延伸，其衛星影像圖和區域地形圖詳見圖1和圖2。滑坡體主軸方向由西南向東北，長1 000 m，寬600 m，高80 m，滑坡體總體積為6 116 000 m3，屬于大型土質堆積層滑坡，其中：Ⅰ級滑坡區域為中區坡前開挖臨空高度12～18 m；Ⅱ級滑坡區域分別為南區坡前開挖臨空高度8～20 m和北區坡前開挖臨空高度5～10 m。該滑坡體在構造上屬于華北地臺鄂爾多斯臺向斜的陜北臺凹，地塊狀態較穩定。地下水類型主要為第四系孔隙與碎屑巖類裂隙水，其分布范圍、富水性與地層巖性、地貌類型與構造因素等密切相關。

圖1 滑坡衛星影像Fig.1 Satellite image of landslide

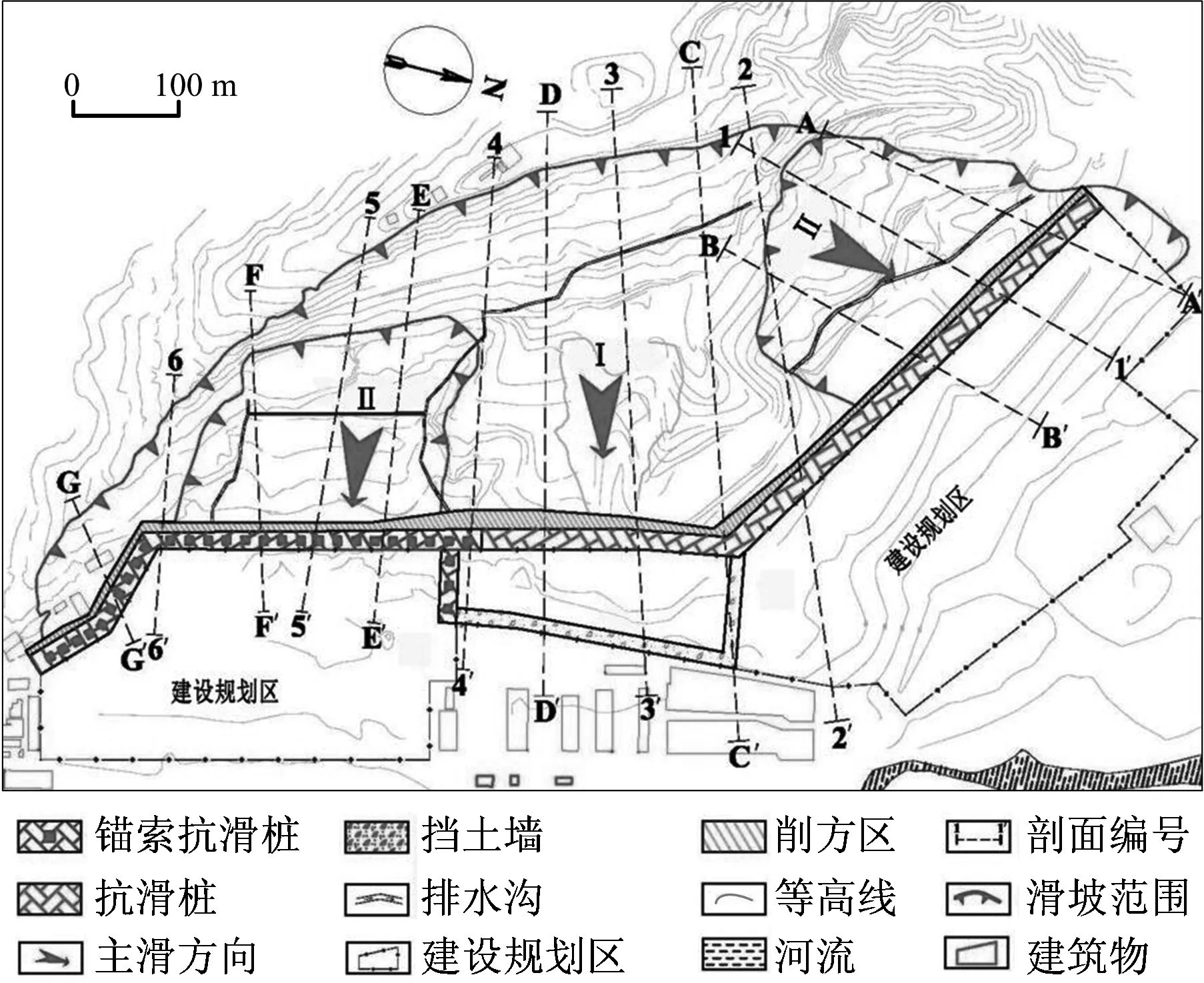
圖2 滑坡區域地形Fig.2 Regional topography of landslide

由于工程項目建設安排，需要對滑坡體前緣進行開挖5～20 m不等，考慮到滑坡體不同區域的開挖高程不同，將會直接影響到坡體的穩定性，進而不可避免地對下游城鎮基礎設施建設和生命財產安全構成重大威脅。鑒于此，為了保證工程項目的順利實施，在項目初步設計階段邀請了8位專家和技術人員，根據滑坡體基本特征、工程重要性和相關規范，經反復論證和比較，在對滑坡體的工程設計、經濟預算、施工周期和環境影響等綜合測評后，給出了8種治理方案(如方案S3在滑坡北區和中區開挖坡腳設置一道截面尺寸1.5 m×2.0 m的抗滑樁，間距6.0 m，懸臂5.0 m，在南區設置一道截面尺寸3.0 m×4.0 m的錨索抗滑樁，間距6.0 m，懸臂10.0 m；同時，對開挖面以上坡體按懸臂部分輔之以坡面和坡體截排水工程；并基于地質災害預警系統實時動態監測，其他方案不再贅述)，其中每一方案均從滑坡體發育特征、危害程度與治理措施等特征出發，從經濟層面、技術層面、風險層面和環境層面進行合理選取和量化(工程投資單位為萬元，U1，U2和U3為成本型指標，U4為效益型指標，由于滑坡體治理方案優選過程中各決策指標的客觀復雜性與不確定性，故采用區間數定量表征決策屬性信息，并以此建立屬性決策矩陣)，具體見表1。

2.2 模型計算與分析

2)利用公式(11)～(12)可求得概率優勢矩陣及其權重度量值如下：

3)利用公式(14)構造加權決策信息見表3。

表1 滑坡治理方案及各指標決策屬性Table 1 Landslide control schemes and decision-making attribute of each index

表2 規范化后決策信息Table 2 Decision-making information after normalization

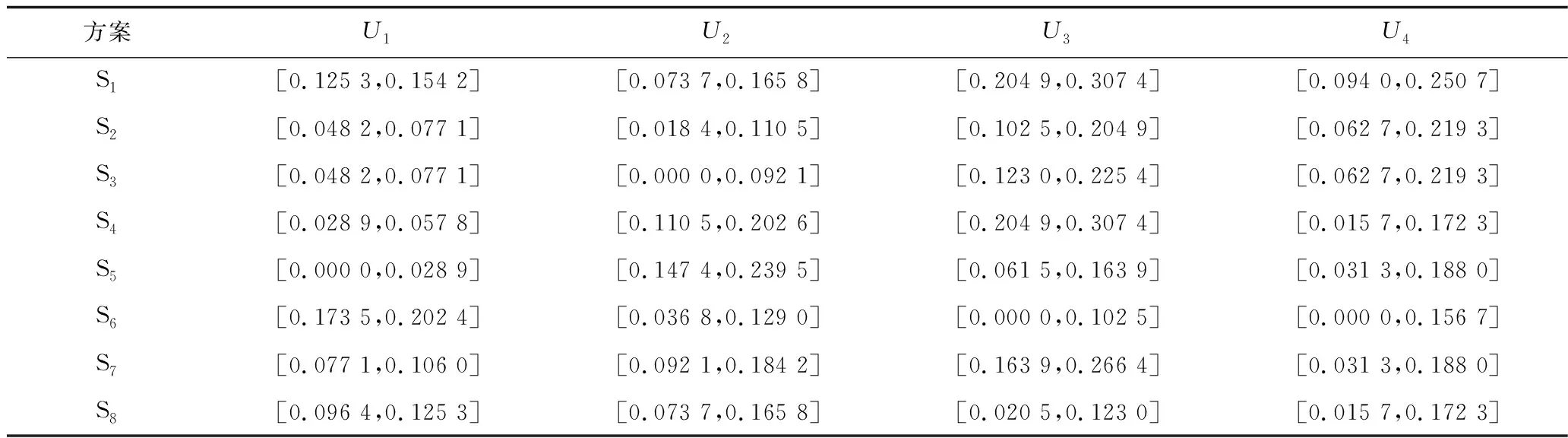
表3 加權決策信息Table 3 Weighted decision-making information

加權綜合屬性值如下：

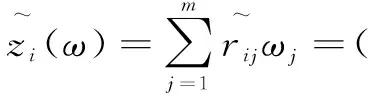
然后按照公式(16)可求得決策方案優勢矩陣為：

4)基于以上決策方案優勢度矩陣Pm×n對此8種治理方案進行優選排序，可得治理方案綜合概率優勢度(0.807 9,0.407 8,0.410 9,0.600 6,0.420 5,0.375 6,…,0.607 3,0.369 4)，根據其綜合概率優勢度大小，可得S1?S7?S4?S5?S3?S2?S6?S8，即S1(重力式擋土墻+漿砌石護坡+地表水治理)為最優方案。

根據推論2中結論及其綜合屬性值，可求得：

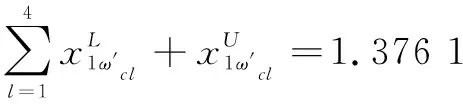
依據推論2對上述治理方案排序如下：

S1?S7?S4?S5?S3?S2?S6?S8

為了對基于區間概率優勢關系的多屬性決策模型進行驗證對比分析，本文采用應用較為廣泛的離差最大賦權法[15]對其賦權，并進行排序擇優，在對治理方案的數據進行規范化處理后，其相應的賦權公式為：

(17)

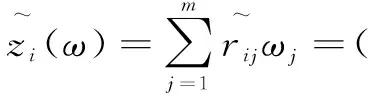
根據基于離差最大算法的多屬性決策模型的計算步驟[15]，利用對其加權綜合屬性值進行兩兩比較的可能度矩陣，如下：

依據該矩陣優選排序的中轉算法，可求得可能度矩陣的排序向量v=(v1,v2,…,vn),i∈N，其中：

利用所求可能度矩陣Pm×n的排序向量大小：v=(0.170 5,0.106 1,0.106 5,0.135 7,0.105 0,0.123 5,0.141 4,0.111 3)因此，可得各滑坡災害治理方案的優選排序為：S1?S7?S4?S6?S8?S3?S2?S5，即S1(重力式擋土墻+漿砌石護坡+地表水治理)為最優方案。綜上，可得幾種決策模型的方案優選排序對比，見表4。

基于上述分析可知：3種模型優選排序結果有所區別，離差最大化算法從決策方案角度出發，對其進行賦權求解，但其忽視了屬性本身的重要程度，導致仿真排序結果不同于另外2種決策模型。本文利用推論2的推理結論進行排序反演，反演結果與區間概率優勢決策模型相同，同時與利用基于離差最大化算法決策方案進行優選對比。結果表明：雖然2種賦權算法的排序部分結果有所不同，但決策方案的最優治理方案均相同。另外，由模型決策過程中的決策屬性矩陣也可看出方案S1在滑坡災害治理過程中的經濟層面、技術層面、風險層面和環境層面優于其他方案，也進一步驗證了所提決策模型的可靠性與科學性。

表4 幾種決策模型方案優選排序對比Table 4 Optimization sorting and comparison of several decision-making model schemes

3 結論

1)滑坡工程治理和方案優選決策一直是地質災害治理領域的研究熱點。結合滑坡災害形成機理及破壞特征，從經濟層面、技術層面、風險層面和環境層面4個層面構建了滑坡災害治理決策系統，為其綜合決策分析奠定基礎。

2)基于合作博弈相關理論，結合概率優勢關系粗糙集相關理論，提出區間概率優勢關系算法的滑坡災害治理優選決策模型，并對其進行理論推導反演，然后將其成功應用到某一滑坡工程治理實例當中。

3)本文所提決策模型評價結果較為客觀地反映了實際工況，且提供了更加豐富的決策信息屬性，也進一步表明其有效性與科學性，可為滑坡災害工程治理方案優選與決策提供借鑒思路。