套管環空壓力恢復與泄壓預測模型研究*

馮 定，周 宇，張 紅，陳文康

(1.長江大學 機械工程學院，湖北 荊州 434023； 2.湖北省油氣鉆完井工具工程技術研究中心，湖北 荊州 434023； 3.非常規油氣湖北省協同創新中心，湖北 武漢 430100)

0 引言

我國天然氣資源豐富，但隨著天然氣開發工作的不斷深入，氣井逐漸呈現出井深、高溫、高壓及高產的特征，而具有上述特征的氣井在生產過程中陸續出現環空帶壓現象[1-2]。環空帶壓，通常又叫持續環空壓力(Sustaind Casing Pressure)，是指氣井環空壓力在泄壓后短時間內又恢復到泄壓前壓力水平的現象[3]。產生環空帶壓的主要原因包括管柱完整性失效、水泥環密封失效和地層漏失[4]。環空帶壓嚴重時會威脅管柱安全，破壞井筒完整性，甚至會導致井口裝置失效，引發泄漏，造成重大安全事故[5-7]。根據環空帶壓發生位置的不同，可以分為油套環空帶壓和套管環空帶壓，本文主要研究了套管間環空壓力的恢復和泄壓過程。

目前國內外關于套管環空壓力恢復的相關研究較多，主要集中在理論研究階段，通過建立各種數學模型對環空帶壓的過程進行模擬預測，然后通過將生產現場的井口壓力變化曲線與理論計算出的壓力變化曲線匹配，從而確定井下一些無法測得的參數，如泄漏深度，泄漏孔的當量大小等，根據匹配的結果來判斷現場井環空帶壓的嚴重程度[8-10]。但現有的環空帶壓數學模型在計算時將液柱段進行了微分，由于井口環空壓力不斷變化，導致液體被壓縮，所以液柱段的長度在不斷變化。這樣就需要不斷更新液柱段的微分，不僅加大了計算難度而且影響了井口環空壓力值的精度。

本文主要通過研究高壓氣體在含微隙水泥環內的滲流規律，求解出了水泥環內氣體的滲流流量。以此為基礎，將水泥環上部的液柱段整體作為研究對象，并不斷進行微分，然后結合氣體運移過程中的質量守恒方程和井口氣柱段的氣體狀態方程，建立了基于水泥環滲流的含液密閉套管環空壓力恢復預測數學模型。該模型計算簡便，考慮液柱段整體的壓縮性，提高了井口環空壓力值的計算精度。并且根據壓力恢復時帶壓值的計算原理，結合泄壓時的井口的嘴流公式，形成了套管環空泄壓預測模型。以現場某A井為例，利用上述模型模擬計算了該井的環空壓力恢復及泄壓過程，并與實測結果進行曲線擬合，能夠確定水泥環的滲透率，并且預測環空帶壓的后續發展趨勢，對套管間環空帶壓的診斷評估和環空壓力的控制具有重要意義。

1 套管環空壓力恢復模型

1.1 水泥環滲流速率計算

通常情況下，水泥環的滲透率很低，氣體在水泥環內的運移過程可以認為是在低滲透性多孔介質內的滲流。而水泥環邊界與地層相連，地層壓力近似認為不變，但水泥環上端出口壓力變化，所以氣體在水泥環中滲流速率隨時間變化，因此水泥環內的滲流過程可以看作是氣體在低滲透固體介質中的不穩定滲流[11-12]。將水泥環離散為無數個如圖1所示的微元立方體，分析氣體在該微元體內的流動過程。

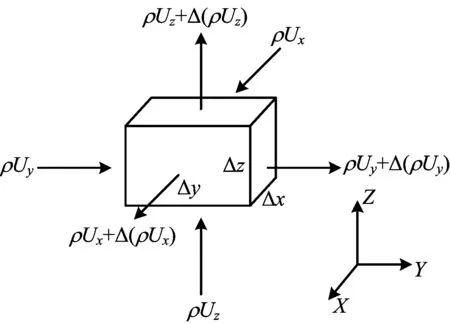
圖1 氣體在水泥環內的滲流微元體示意Fig.1 Schematic diagram of the micro-element of gas seepage in the cement sheath

由于氣體在水泥環內主要向上運移，所以本文假設在如圖1所示微元體的x和y方向上沒有介質流動，所以氣體在z方向上一維流動的滲流連續性方程為：

(1)

式中：ρ為氣體密度，kg/m3；uz為氣體在z方向上的速度，m/s；φ為介質的孔隙度。

氣體在水泥環內滲流時，溫度、氣體黏度和壓縮因子的變化都很小，可認為是等溫達西滲流，所以氣體滲流的運動方程為：

(2)

根據氣體在水泥環內的連續性方程和運動方程，并結合氣體的狀態方程，通過求解，最終得關于氣體在水泥環內的滲流速率：

(3)

式中：Q1為水泥環內氣體滲流速率，m3/d；k為水泥環滲透率，10-3μm2；μ為氣體黏度，mPa·s；Pf為產層壓力，MPa；Pc為水泥環與泥漿接觸面處壓力，MPa；A為水泥環截面積，m2；Psc為標準狀態下的氣體壓力，0.101 MPa；Tsc為標況下的氣體溫度，273.15 K；Tf為產層溫度，K；L為水泥環長度，m；Z為氣體偏差因子。

1.2 壓力恢復時套管環空帶壓值計算

氣井套管環空帶壓期間，氣體的運移過程如圖2所示，產層高壓氣體通過水泥環的微隙向上滲流，依次通過水泥環、泥漿，然后在井口聚集[13-15]。

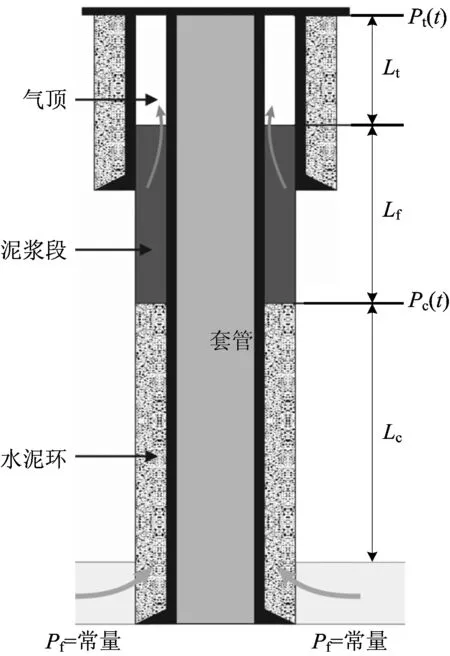
圖2 氣體泄漏過程Fig.2 Gas leakage process

在模型建立過程中，忽略了氣體在泥漿段的運移過程，將整個環空壓力恢復周期分為若干個微元段，則在第n個時間段內井口氣柱段的PVT方程為：

(4)

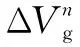
(5)

氣體物質的量的變化量為：

(6)

(7)

式中：pt為套管環空井口壓力，MPa；ng為套管環空井口氣體的物質的量，mol；Vg為套管環空氣柱體積，m3；Vm為套管環空液柱體積，m3；Psc為標準狀態下的氣體壓力，0.101 Mpa；Tsc為標況下的氣體溫度，273.15 K；cm為泥漿壓縮系數，MPa-1；R為氣體常數，8.314×10-6m3·MPa/(K·mol)；Z為氣體偏差因子；Twh為套管環空井口溫度，K；Δt為單位時長，d。

2 套管環空泄壓模型

2.1 井口泄壓氣體速率計算

一般通過打開氣井井口的針型閥泄放掉環空井口聚集的氣體，假設環空泄壓時針型閥處為單相氣體流動，則氣體流過針型閥的節流示意圖如圖3所示。對于壓縮流體的節流過程通常分為2種狀態：若流體在節流后流速達到聲速，則稱為臨界流動；若節流后流速小于聲速，則稱為亞臨界流動[16]。

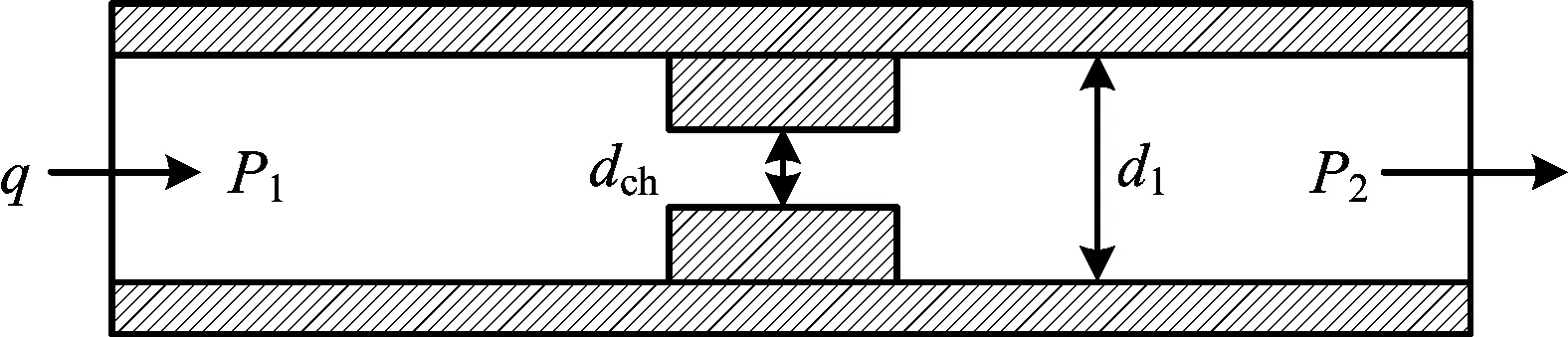
圖3 節流過程示意Fig.3 Schematic diagram of throttle process

一般通過針型閥下、上游壓力之比判別針型閥處氣體的流動狀態[17-19]。

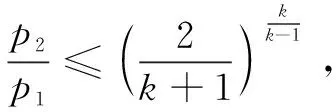
(8)

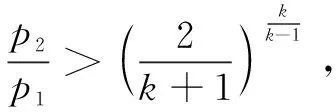
(9)

式(8)～(9)中：Q2為標況下針型閥氣體流量，m3/d；p1為針型閥上游壓力，MPa；p2為針型閥下游壓力，MPa；dch為針型閥的開度，mm；T1為井口溫度，K；γg為氣體相對密度；Z為氣體偏差因子；k為天然氣氣體絕熱指數，通常取1.28。

2.2 泄壓時套管環空帶壓值計算

泄壓時套管環空帶壓值的計算方法和壓力恢復時的一樣，均以井口氣柱段作為研究對象。由于泄壓時針型閥處的氣體排放流量遠大于此時從水泥環泄漏至井口的氣體流量，所以在建立泄壓模型時，忽略水泥環泄漏至井口的氣體。則在第n個時間段內井口氣柱段的PVT方程為：

(10)

其中：

(11)

(12)

(13)

式中：pt為套管環空井口壓力，MPa；ng為套管環空井口氣體的物質的量，mol；Vg為套管環空氣柱體積，m3；Vm為套管環空液柱體積，m3；Psc為標準狀態下的氣體壓力，0.101 Mpa；Tsc為標況下的氣體溫度，273.15 K；cm為泥漿壓縮系數，MPa-1；R為氣體常數，8.314×10-6m3·MPa/(K·mol)；Z為氣體偏差因子；Twh為套管環空井口溫度，K；Δt為單位時長，d。

3 現場應用

3.1 基本參數

A井完井深度為5 200 m，封隔器深度為4 500 m，儲層溫度134.83～143.74 ℃，儲層壓力76.3 MPa。該井日產氣量274×104m3，套管環空井口的初始壓力為0.17 MPa，溫度為20 ℃。其具體的相關參數見表1。

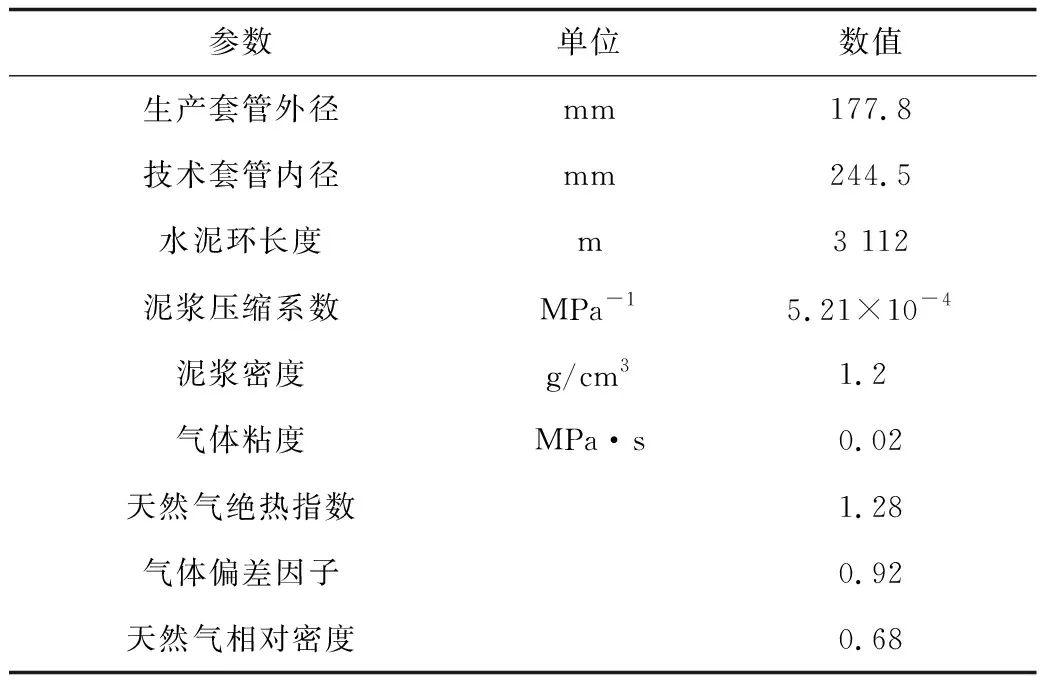
表1 A井井身結構和流體相關參數Table 1 Related parameters of well structure and fluid for “A” well

3.2 模型驗證與分析

以A井為例，根據該井的井身結構、生產數據和流體參數，利用上述的套管環空壓力恢復預測模型，模擬該井的套管環空帶壓過程，結果如圖4所示。通過計算得環空壓力的計算值與實測值之間的平均相對誤差不超過7%，計算結果和實測壓力上升曲線基本吻合，說明了該模型具有較高的準確性。分析圖4的計算結果可知，隨著井口帶壓值的不斷上升，水泥環的氣體滲流流量不斷減小，當滲流流量趨于0時，井口帶壓值趨于平穩。通過與測試數據進行擬合，預估出該井套管環空內的井口氣柱約為10 mm，殘留泥漿約高為2 mm，水泥環的滲透率約為100 md，為套管環空帶壓的診斷評估提供了理論依據。

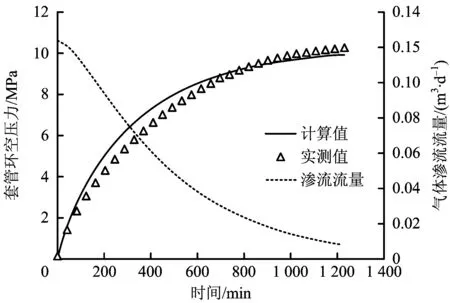
圖4 A井套管環空壓力恢復計算結果Fig.4 Calculation result of casing annular pressure recovery for “A” well

根據上述套管環空壓力恢復的計算結果，最終該井套管環空井口的穩定帶壓值約為10.3 MPa，以壓力恢復的計算結果作為初始條件，利用上述套管環空泄壓預測模型，模擬該井的套管環空泄壓過程，結果如圖5所示。通過計算得環空壓力的計算值與實測值之間的平均相對誤差不超過21.4%，分析產生較大誤差的原因為泄壓過程過快導致實測數據較少，計算值與實測值之間缺乏對比。通過對泄壓過程的模擬，能夠有效預測泄壓所需的時間，為現場環空的泄壓作業提供一定的理論指導，提高了泄壓過程的安全性。

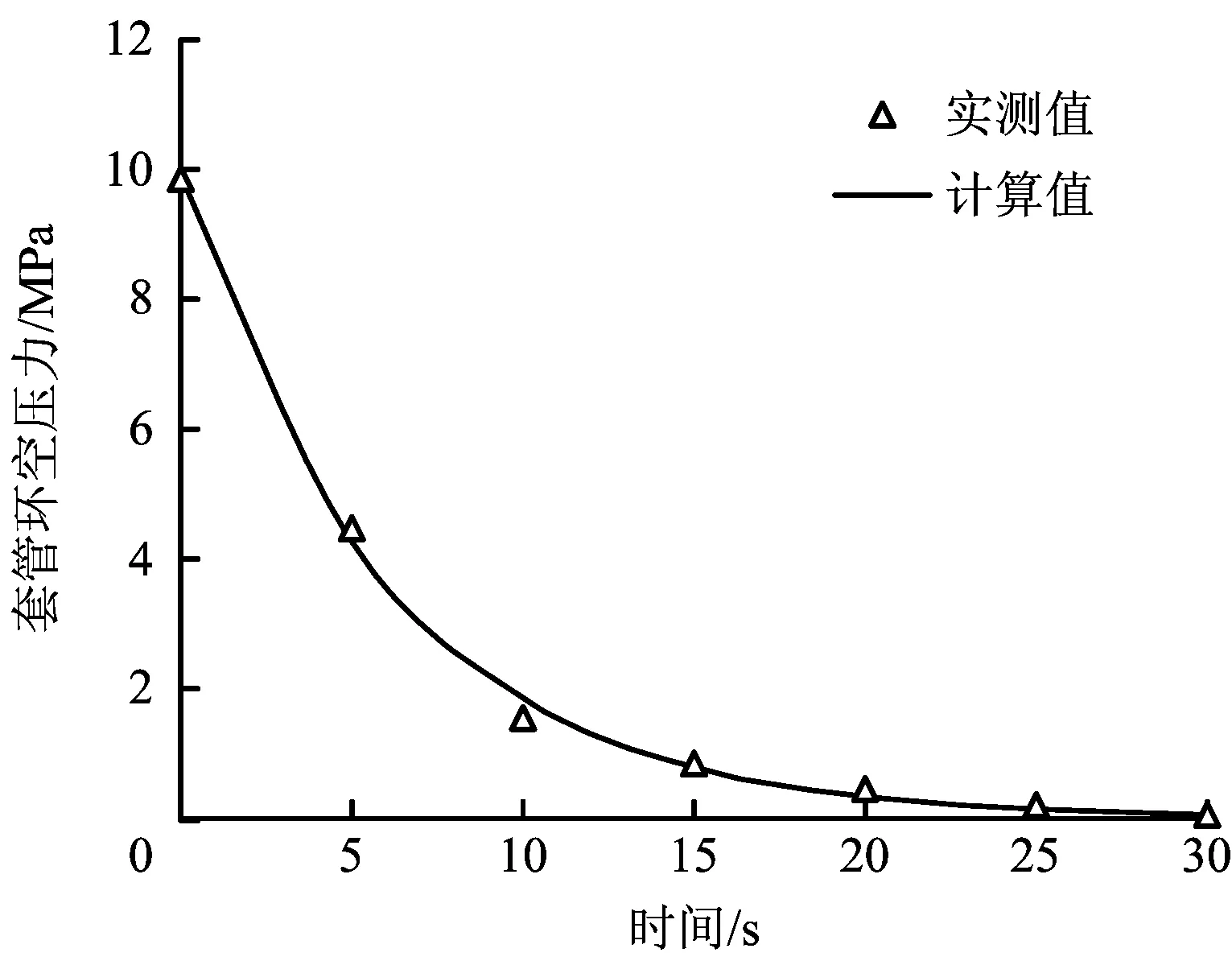
圖5 A井套管環空泄壓計算結果Fig.5 Calculation result of casing annular pressure relief for “A” well

4 結論

1)以套管環空水泥環內的氣體為研究對象，建立了氣體滲流的連續性方程和運動方程，并求解出了氣體在水泥環中的滲流速率。以此為基礎，考慮液柱段整體的壓縮性，結合井口的氣體狀態方程，建立了套管環空壓力恢復預測模型。

2)根據嘴流公式計算出井口泄壓時針型閥處氣體的流量，結合壓力恢復過程中帶壓值的計算方法，建立了套管環空壓力泄壓預測模型。

3)以A井為例，根據該井的井身結構、生產數據和流體參數，結合本文的套管環空壓力恢復和泄壓預測模型，模擬計算了A井的壓力恢復和泄壓過程。結果表明：模擬計算值和現場的實測值基本吻合，模型具有較高的準確性。