例說解三角形中與正切函數有關的最值問題
☉廣東省高州中學 吳永福
三角形中與正切函數有關的最值問題曾經出現在2016年的江蘇高考試題中,近年來在許多高考模擬試題中,又出現了這樣的題型,該題型不屬于常見題型,對許多人來說比較陌生,難處理,那么如何解這類題型?筆者對這類題型的解法進行了探究,揭示了其存在的一些解題規律,在此與各位分享,望能對各位的解題有所幫助.
類型一、目標函數為正切函數
①目標函數為tanAtanBtanC,條件可化簡為tanA+tanB=mtanAtanB(或tanA+tanC=mtanAtanC或tanB+tanC=mtanBtanC)
例1 在銳角三角形ABC中,若sinA=2sinBsinC,則tanAtanBtanC的最小值是______.

小結:由sinA=2sinBsinC 變形得到tanB+tanC=2tanBtanC,將tanAtanBtanC表示成關于tanBtanC的函數,再求其最小值.
②目標函數為tanAtanBtanC,條件可化簡為tanA=mtanB(或tanA=mtanC或tanB=mtanC)
例2在銳角三角形ABC中,角A,B,C所對的邊分別為a,b,c,已知a2+2abcosC=3b2,則tanAtanBtanC的最小值為______.


小結:利用公式sin2A-sin2B=sin(A+B)sin(A-B)化簡,得 到tanA=3tanB,將tanC 也 用tanB 表 示,將tanAtanBtanC表示成關于tanB的函數,再求其最小值.
例3在銳角三角形ABC中,已知2sin2A+sin2B=2sin2C,則的最小值為______.

小結:根據系數關系將2sin2A+sin2B=2sin2C變形為sin2B=2(sin2C-sin2A),利用公式sin2C-sin2A=sin(C+A)·sin(C-A)化簡,得到tanC=3tanA,將tanB也用tanA表示,將表示成關于tanA的函數,再求其最小值.
類型二、目標函數可轉化為正切函數
例4銳角△ABC的面積為1,則的最小值為______.

小結:利用三角形的面積為1,將b2用角表示,將用角表示,再利用公式進行化簡,得到,根據,得到·,利用均值不等式求得的最大值,從而得到的最小值.
類型三、條件中含正切函數
例5已知在△ABC中,a,b,c分別為三個內角A,B,C的對邊,若tanA=2tanB,則的最大值為______.

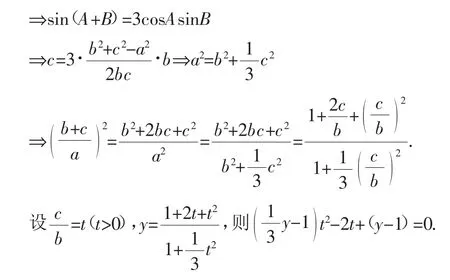
小結:將tanA=2tanB 切化弦,變形為sinAcosB=2cosAsinB,再配湊為sin(A+B)=3cosAsinB,即sinC=3cosAsinB,用正、余弦定理轉化為邊的關系,再求的最大值.
例6已知△ABC的面積為,且滿足,則邊AC的最小值為______.

小結:將切化弦,表示成2cosAsinB+sinAcosB=sinAsinB,配 湊 成sin(A+B)+cosAsinB=sinAsinB,即sinC=(sinA-cosA)sinB,用正弦定理轉化成c=(sinA-cosA)b,利用三角形的面積公式,將邊b表示成角A的函數,從而可求出其最小值.

