精確的電力系統故障計算
陳朝煜
(福建省機電建筑設計研究院 福建福州 350001)
0 引言
在電力系統進行故障精確計算時,需要計及發電機直軸次暫態電抗(xd″)與交軸次暫態電抗(xq″)的差別,目前只有單臺發電機機端或出線故障計算才能考慮到這個問題,如果是多機網絡用對稱分量法進行故障計算還無法解決這個問題。文獻[1]用修改導納矩陣法計算故障也存在這個問題。本文以修改導納矩陣法為基礎,進行一些改進使之能計及發電機直軸次暫態電抗與交軸次暫態電抗的差別。
修改導納矩陣法的思路,是故障瞬間網絡節點的注入電流保持不變,唯一發生變化是網絡結構和參數,即導納矩陣發生變化,將故障部分的導納矩陣疊加到正常導納矩陣上,形成故障時的導納矩陣。然后,求解故障時的節點三序網絡方程,便可求得節點三序電壓,從而計算出各節點的三相電壓和各支路電流。下文首先將復數的節點三序網絡方程用直角坐標表示變為實數方程,然后將各發電機以直軸(d)和交軸(q)表示的回路方程通過轉子位置角變換為系統公共坐標的方程,使發電機的回路方程融入系統正序網絡實數方程,最后求解新的三序網絡實數方程,求得節點的三序電壓。
1 三序網絡方程
文獻[2]導納型的節點三序網絡方程有兩種表達方式,第一種是按節點塊排列,即:
(1)
第二種是按序網塊排列,即:
(2)
式(2)中:U1為正序網節點電壓列向量;U2為負序網節點電壓列向量;U0為零序網節點電壓列向量;I1為正序網節點注入電流列向量;I2為負序網節點注入電流列向量;I0為零序網節點注入電流列向量;YⅠ為正序網節點導納矩陣;YⅡ為負序網節點導納矩陣;Y0為零序網節點導納矩陣;YⅠⅡ為正序網與負序網節點之間的耦合導納矩陣;YⅠ0為正序網與零序網節點之間的耦合導納矩陣;YⅡⅠ為負序網與正序網節點之間的耦合導納矩陣;YⅡ0為負序網與零序網節點之間的耦合導納矩陣;Y0Ⅰ為零序網與正序網節點之間的耦合導納矩陣;Y0Ⅱ為零序網與負序網節點之間的耦合導納矩陣。上述各序電壓、電流列向量均為n維向量,各序及序間導納矩陣均為n×n階矩陣。當網絡結構是對稱時,各序間的耦合導納矩陣皆為零矩陣。只有網絡結構不對稱時,各序間才會出現耦合導納。
式(2)的展開式為:
(3)
i=1,2,3,…,n;m=1,2,0;s=1,2,0
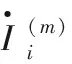
式(3)用直角坐標表示,可改寫為:
(4)
i=1,2,3,…,n;m=1,2,0;s=1,2,0
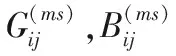
將式(4)改寫成實數方程,即:
(5)
i=1,2,3,…,n;m=1,2,0;s=1,2,0
2 發電機回路方程
(6)
由潮流計算求得的電壓和電流所處的坐標稱為系統公共坐標,它們用直角坐標表示為:
(7)
參考文獻[3],確定發電機轉子位置角。虛構電動勢為:
(8)
式(8)中:r為定子電阻;xq為交軸電抗;δ是轉子位置角,即發電機q軸與系統x軸之間的夾角。
發電機定子電壓和電流的d、q軸分量與系統公共坐標x、y軸分量的關系如圖1所示,其關系如下:

圖1 d,q軸分量與x,y軸分量關系圖
(9)
(10)
由式(9)、式(10)可求得正常運行發電機d、q軸電壓和電流。
參考文獻[3],按下式計算發電機的直軸次暫態電勢和交軸次暫態電勢,即:
(11)
式(11)中:r為定子電阻,xd″為直軸次暫態電抗,xq″為交軸次暫電抗。
由式(8)、式(11)可求得正常運行發電機的轉子位置角δ、直軸次暫態電勢Ed″和交軸次暫態電勢Eq″。
(2)故障瞬間:發電機有這樣的特性,即故障瞬間轉子位置角和直、交軸次暫態電勢不會發生突變,可由上述正常運行求得。轉子位置角和直、交軸次暫態電勢成為故障計算的已知量,而電壓和電流成為待求量。
故障瞬間發電機定子回路方程與正常運行時的表達方式是一樣的,如式(11)所示,可改寫為:
(12)
其中,發電機dq坐標的阻抗矩陣的逆矩陣為
(13)
稱為發電機dq坐標的導納矩陣。
式(11)、式(12)稱為發電機dq坐標的回路方程,通過式(9)、式(10)可把它轉換為發電機公共坐標的回路方程,即將式(9)、式(10)和式(13)代入式(12),可得:
(14)
其中,IGx″和IGy″稱為發電機等值電流源的電流,也是正序網絡發電機節點的注入電流,它們的表達式為:
(15)
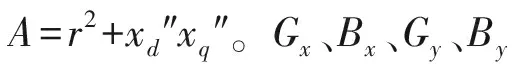
(16)
設發電機的節點為i,將發電機的回路方程式(14)代入系統網絡方程式(5),可得對應于正序網發電機節點的方程式為:
(17)
電力系統故障計算修改導納矩陣法的核心是解故障瞬間系統的網絡方程,方程中的導納矩陣是由正常運行的導納矩陣和故障部分的修改導納矩陣組成,節點的注入電流只有正序網的發電機節點和用發電機表示的負荷節點才有注入電流,正序網的其他節點和負序網與零序網所有節點的注入電流均等于零。修改導納矩陣法解的網絡方程是復數方程,這里要解的網絡方程是實數方程。實數方程分為兩種情況,第一種情況是正序網的發電機節點和用發電機表示的負荷節點采用的網絡方程是本文方程式(17),第二種情況是非上述節點采用的網絡方程是本文方程式(5)。
3 故障計算原理
設故障前,即正常運行時,電力系統三序網絡方程為:
Y(0)U(0)=I(0)
(18)
故障瞬間電力系統三序網絡方程為:
Y(f)U(f)=I(f)
(19)
式(18)(19)中:U(0)是正常運行時網絡節點三序電壓列向量;I(0)是正常運行時網絡節點注入三序電流列向量;Y(0)是正常運行時網絡節點三序導納矩陣;U(f)是故障瞬間網絡節點三序電壓列向量;I(f)是故障瞬間網絡節點注入三序電流列向量;Y(f)是故障瞬間網絡節點三序導納矩陣。
方程式(18)、式(19)的結構與方程式(1)、式(2)相同。
由于故障發生瞬間發電機的次暫態電動勢不會發生突變,其等值電流源的電流也不會發生突變,發電機節點的注入電流也就不會突變,所以故障瞬間網絡節點注入三序電流列向量I(f)等于正常運行時網絡節點注入三序電流列向量I(0),即:
I(f)=I(0)
(20)
發生故障瞬間唯一發生變化的是電力網絡的結構和參數,即節點三序導納矩陣發生變化。由于導納矩陣具有可疊加性,所以故障瞬間網絡節點三序導納矩陣Y(f)可以由正常運行時網絡節點三序導納矩陣Y(0)和故障部分修改導納矩陣ΔY(f)疊加而成,即:
(21)
其中,nf是故障重數。
方程中節點的注入電流只有正序網的發電機節點和用發電機表示的負荷節點才有注入電流,正序網的其他節點和負序網與零序網所有節點的注入電流均等于零。修改導納矩陣法解的網絡方程是方程(19),是復數方程;而精確的電力系統故障計算要解的網絡方程是方程式(5)和式(17),是實數方程。解實數方程分兩種情況,第一種情況是正序網的發電機節點和用發電機表示的負荷節點采用的網絡方程是方程式(17),第二種情況是非上述節點采用的網絡方程是方程式(5)。應該注意,方程式(5)、式(17)中的導納是故障瞬間網絡節點三序導納矩陣中的元素。
精確故障計算與修改導納矩陣法不同之處:
(1)修改導納矩陣法中發電機用次暫態電勢E″和直軸次暫態電抗xd″計算發電機節點的注入電流(參考文獻[2]),精確故障計算中發電機用直軸次暫態電勢Ed″、交軸次暫態電勢Eq″、直軸次暫態電抗xd″和交軸次暫態電抗xq″計算發電機節點的注入電流,參見式(15)。這說明精確故障計算更真實地反映發電機的實際情況,使之計算更精確。
(2)精確故障計算中采用式(16)計算發電機的自導納,修改導納矩陣法用阻抗r+jxd″計算發電機的自導納。
(3)修改導納矩陣法用復數方程式(19)描述;精確故障計算用實數方程式(5)和式(17)描述。
4 故障計算步驟
(1)輸入原始數據。
(2)形成正常運行導納矩陣。
(3)進行潮流計算,求得各節點電壓和功率。
(4)按式(8)、式(11)計算各發電機的轉子位置角,直軸次暫態電勢和交軸次暫態電勢。
(5)按式(15)、式(16)計算發電機的注入電流和自導納。
(6)輸入故障信息,形成故障部分的修改導納矩陣。
(7)形成故障瞬間系統的導納矩陣,包括發電機的自導納。
(8)解網絡方程式(5)和式(17),求得各節點三序電壓。
(9)計算各節點三相電壓和各支路三序電流、三相電流。
5 仿真計算
根據上述故障計算原理進行計算機仿真計算。現以文獻[2]提供的22個節點,35條支路,6臺發電機,8個負荷的電力系統為例進行計算,如圖2所示, 其中,支路參數如表1所示,發電機功率和參數如表2所示,負荷功率如表3所示,所有數據均為標幺值。
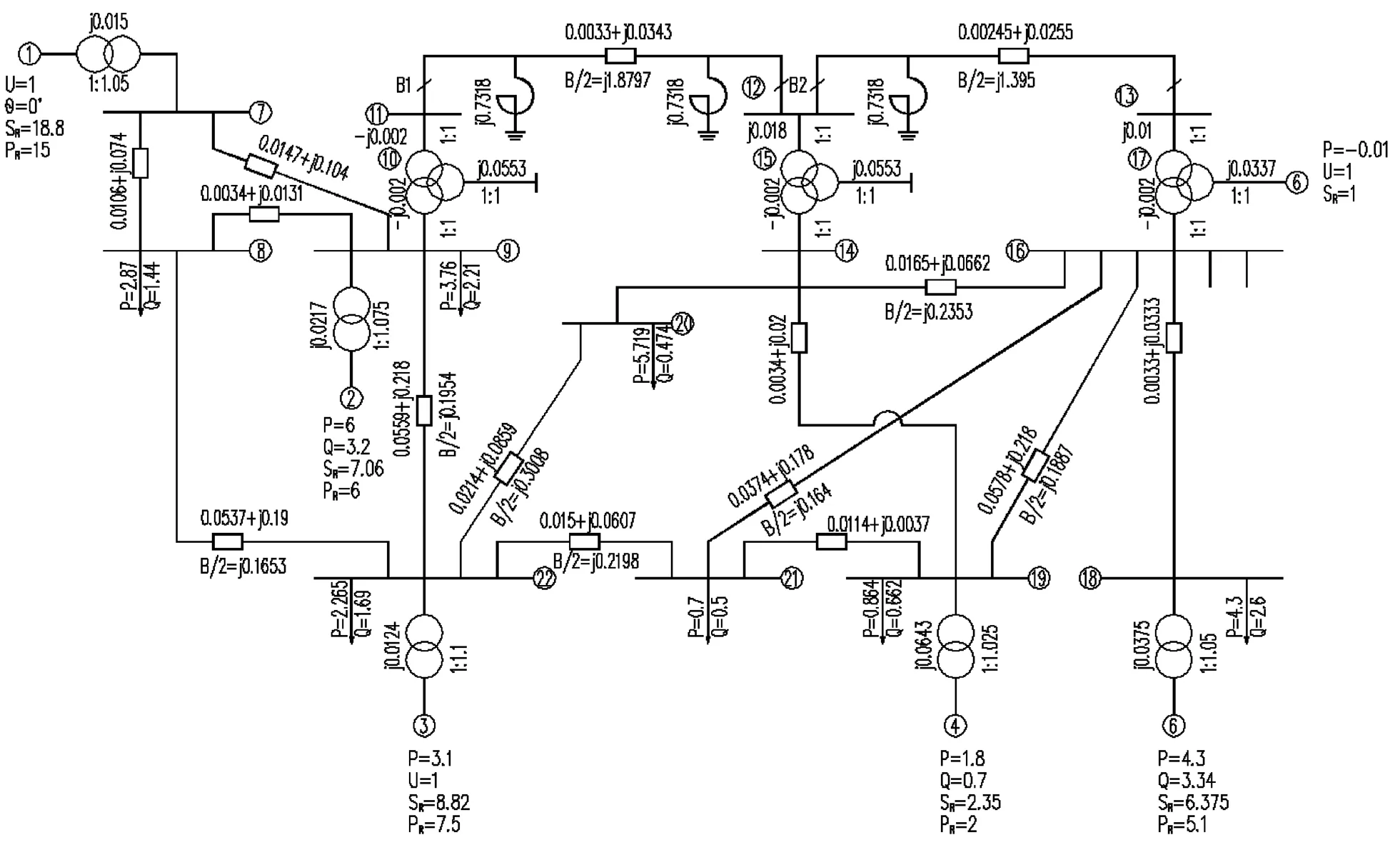
圖2 某一電力系統正序網絡接線圖
表1 支路參數
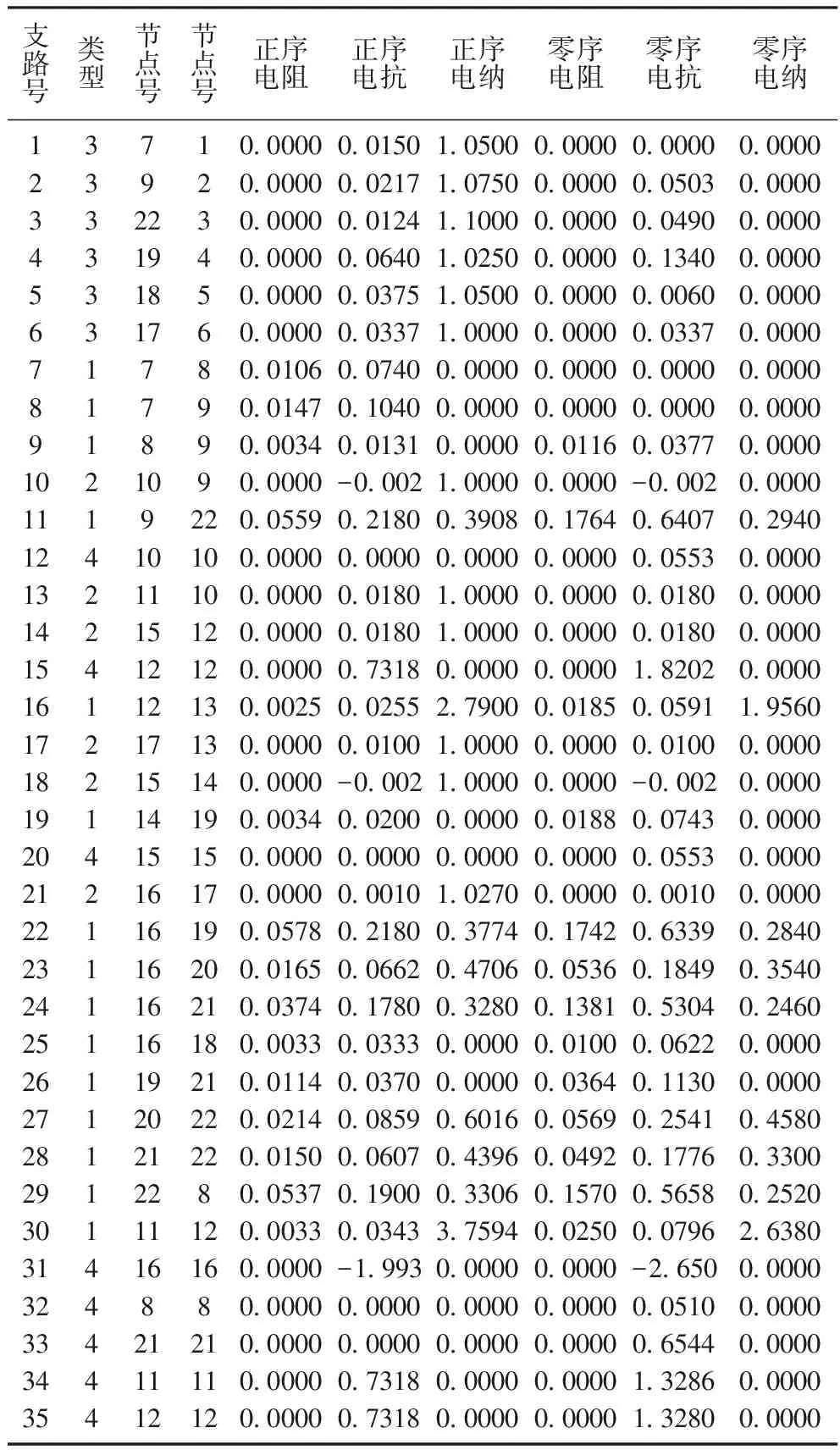
支路號類型節點號節點號正序電阻正序電抗正序電納零序電阻零序電抗零序電納13710.0000 0.0150 1.0500 0.0000 0.0000 0.0000 23920.0000 0.0217 1.0750 0.0000 0.0503 0.0000 332230.0000 0.0124 1.1000 0.0000 0.0490 0.0000 431940.0000 0.0640 1.0250 0.0000 0.1340 0.0000 531850.0000 0.0375 1.0500 0.0000 0.0060 0.0000 631760.0000 0.0337 1.0000 0.0000 0.0337 0.0000 71780.0106 0.0740 0.0000 0.0000 0.0000 0.0000 81790.0147 0.1040 0.0000 0.0000 0.0000 0.0000 91890.0034 0.0131 0.0000 0.0116 0.0377 0.0000 1021090.0000 -0.0021.0000 0.0000 -0.002 0.0000 1119220.0559 0.2180 0.3908 0.1764 0.6407 0.2940 12410100.0000 0.0000 0.0000 0.0000 0.0553 0.0000 13211100.0000 0.0180 1.0000 0.0000 0.0180 0.0000 14215120.0000 0.0180 1.0000 0.0000 0.0180 0.0000 15412120.0000 0.7318 0.0000 0.0000 1.8202 0.0000 16112130.0025 0.0255 2.7900 0.0185 0.0591 1.9560 17217130.0000 0.0100 1.0000 0.0000 0.0100 0.0000 18215140.0000 -0.0021.0000 0.0000 -0.0020.0000 19114190.0034 0.0200 0.0000 0.0188 0.0743 0.0000 20415150.0000 0.0000 0.0000 0.0000 0.0553 0.0000 21216170.0000 0.0010 1.0270 0.0000 0.0010 0.0000 22116190.0578 0.2180 0.3774 0.1742 0.6339 0.2840 23116200.0165 0.0662 0.4706 0.0536 0.1849 0.3540 24116210.0374 0.1780 0.3280 0.1381 0.5304 0.2460 25116180.0033 0.0333 0.0000 0.0100 0.0622 0.0000 26119210.0114 0.0370 0.0000 0.0364 0.1130 0.0000 27120220.0214 0.0859 0.6016 0.0569 0.2541 0.4580 28121220.0150 0.0607 0.4396 0.0492 0.1776 0.3300 2912280.0537 0.1900 0.3306 0.1570 0.5658 0.2520 30111120.0033 0.0343 3.7594 0.0250 0.0796 2.6380 31416160.0000 -1.9930.0000 0.0000 -2.6500.0000 324880.0000 0.0000 0.0000 0.0000 0.0510 0.0000 33421210.0000 0.0000 0.0000 0.0000 0.6544 0.0000 34411110.0000 0.7318 0.0000 0.0000 1.3286 0.0000 35412120.0000 0.7318 0.0000 0.0000 1.3280 0.0000
注:支路類型:1表示輸電線路;2表示YN/yn變壓器;3表示Y/Δ變壓器;4表示對地支路。
正序電納項:輸電線路為正序電納;變壓器為非標準變比。
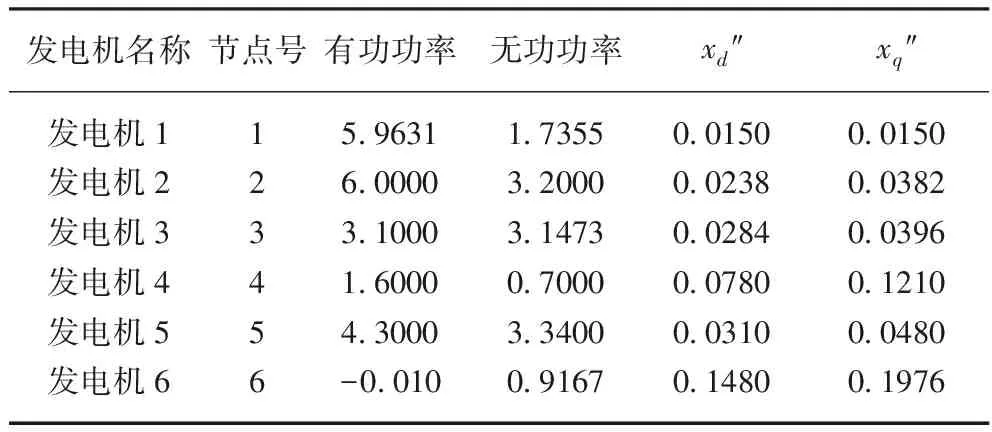
表2 發電機功率與參數

表3 負荷功率
先以三相短路為例,用兩種計算方法各自進行計算。第一種方法,發電機采用xd″進行計算;第二種方法是本文提出的方法,即發電機采用xd″與xq″進行計算,其結果列在表4中。
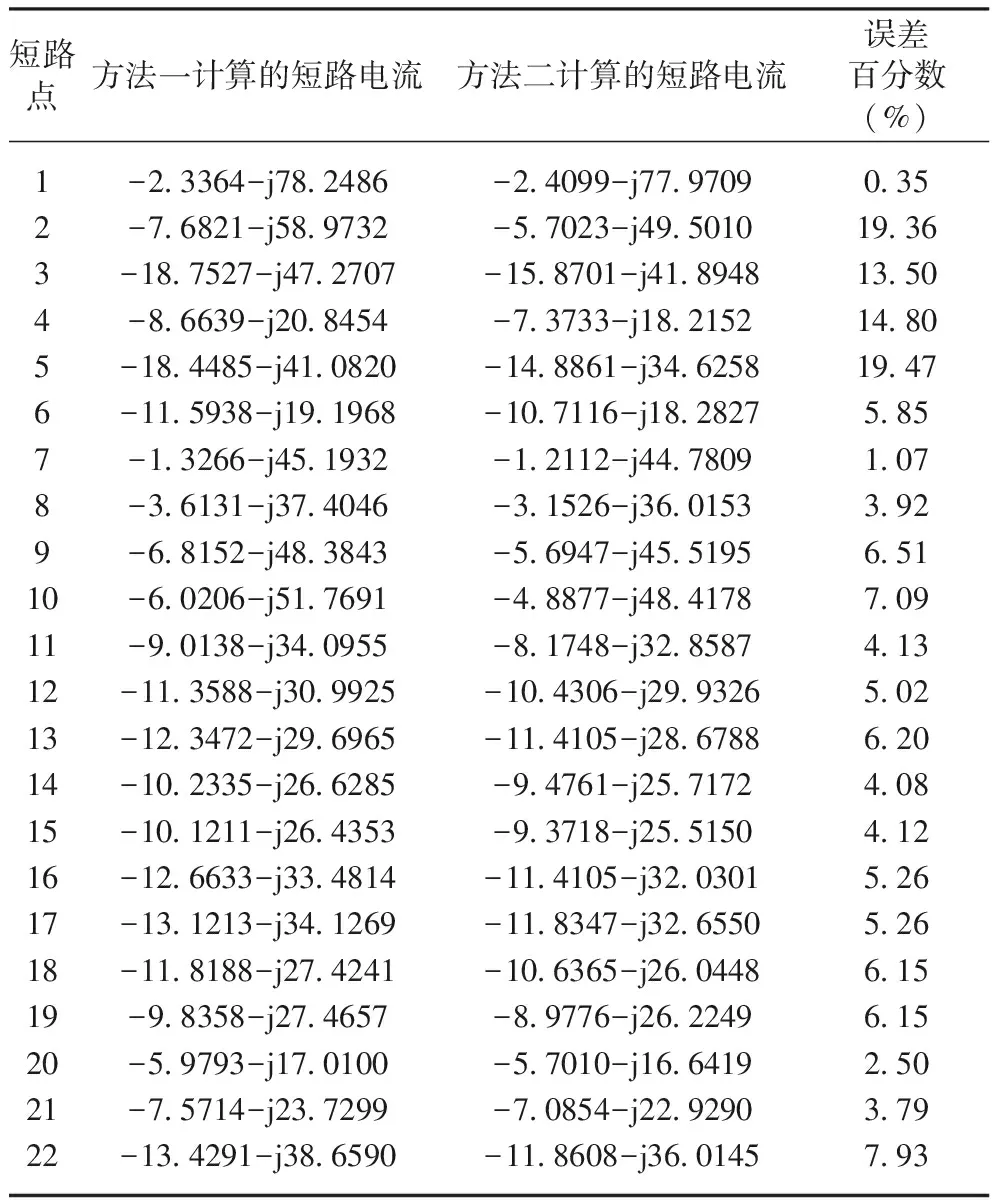
表4 三相短路電流計算結果
注:誤差百分數是以第二種方法計算的電流幅值為基值,第一種計算方法計算的電流幅值由偏移值計算出來。
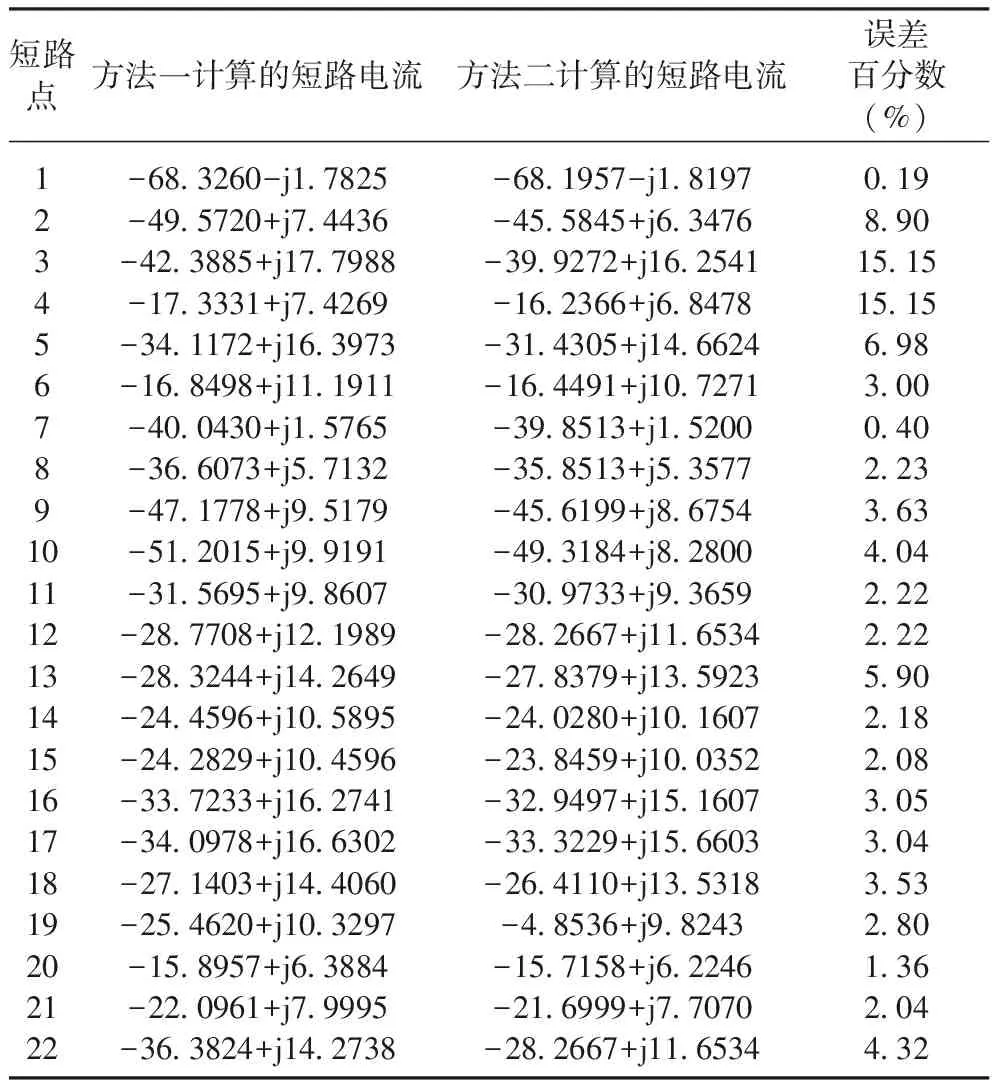
表5 兩相短路電流計算結果
比較兩個計算結果,不難發現不考慮發電機直軸次暫態電抗與交軸次暫態電抗的差別會帶來一定的誤差。這些誤差與故障地點、發電機參數等因素有關,特別發電機xd″與xq″差別較大且靠近發電機的節點發生短路時,其誤差很大,在要求精確計算的場合,建議采用本文提出的精確計算方法。
6 結語
在電力系統故障精確計算中應計及發電機直軸次暫態電抗xd″與交軸次暫態電抗xq″的不同,但現有所有故障計算方法中都未能考慮到這個問題,即發電機均用直軸次暫態電抗xd″進行計算。本文在修改導納矩陣法的基礎上,作出一些改進,將復數的節點三序網絡方程用直角坐標表示變為實數方程,然后將各發電機以直軸(d)和交軸(q)表示的回路方程通過轉子位置角變換為系統公共坐標的方程,使發電機的回路方程融入系統正序網絡實數方程中來,最后求解新的三序網絡實數方程,求得節點的三序電壓。新的三序網絡實數方程能計及發電機直軸次暫態電抗xd″與交軸次暫態電抗xq″的差別,這樣可以提高故障計算的精度,而且未增加計算工作量。

