物理力學解題中整體法的巧妙應用思考
曾斯成
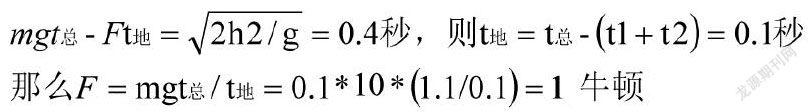
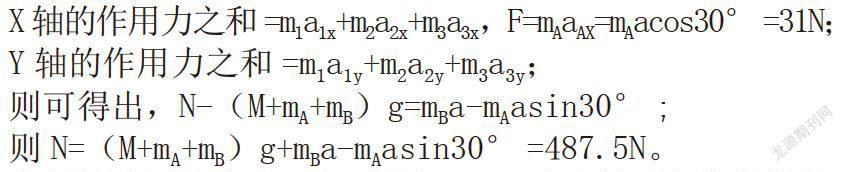
摘 要:力學作為高中物理學習過程當中的重點內容,更是進行學習的難點,需要全面考慮各個物體之間的受力關系和運動變化。而在高中物理力學解題當中運用整體法,不僅能有效解決物理力學問題,還具有著較高的使用價值。本文主要針對在物理力學解題中整體法的應用方式展開較為深入的分析,希望能為相關人士提供些許參考。
關鍵詞:高中物理;力學解題;整體法;應用
引言:在高中物理解題的過程當中,整體法具有較為廣泛的應用價值,而在高中物理學習當中,力學則是占有著重要地位。那么在物理學解題過程當中合理運用整體法,則是能夠有效的針對大部分力學題進行解決,從而把物體之間受力的復雜討論情況進行省略,在最短的時間當中快速找到力學題目的中心點,進而提升自身的物理力學解題效率。
一、整體法的主要概念
整體法主要是指把多個受力的物體作為一個整體,從而在把他們相互之間所形成的作用力作為一個系統當中的內在力,進而針對受力分析過程開始簡化,有效減少受力的分析對象。而且整體法還是作為高中學生進行學習物理知識的解題方法,能夠和隔離法并列成為高中物理力學解題主要方法。那么由于物理力學內容過于復雜且難點較多,所以這就需要合理運用整體法的方式,快速找到力學題目的中心點,從而簡化力學題目的難度,以此來提升自身的解題效率,但是在運用整體法進行解決力學問題的時候,不能夠隨便進行使用,而是應當在自身已經完全了解和掌握題目含義的時候,確定該題目是在整體法的使用范圍當中,才能進行使用[1]。
二、物理力學解題中整體法的應用方式
1.全面培養自身的整體思維
根據當前我國高中物理力學學習現狀來看,有很多學生都在解題的過程當中高度重視某個局部問題,從而忽視了全方面的思考,最終導致漏算漏計等問題時常出現。針對上述情況就應當培養自身的整體思維。
例如:教師給學生出的一道題目,讓學生進行思考當一個球從1.8米的高處進行自由下降的時候,在觸碰到地面時又產生了向上彈起的現象,其彈起的高度最大值為0.8米,那么假設在球體下降的時候一共是用時1.1秒,而球體的質量則是為0.1千克,這就需要進行分析當球體和地面之間產生碰撞的時候,地面針對球體所產生的平均作用力是多少。
解析:當學生進行解決這一問題的時候,就可以合理運用整體法解題方式進行解決。球體在整個自由下降的過程當中只是遭受到了重力的作用,那么就可以把整個球體下降彈起再到落地的過程當作是整個過程,得出下列結果:
將從整體的角度進行分析,要把復雜的物理過程進行有效簡化,進而不僅能有效減少自己的解題時間,還能有效提升自身的解題效率[2]。
2.物體平衡題型當中的應用
在高中物理知識的學習和高考過程當中,物理平衡問題占有著重要位置,平衡問題則是主要進行考察學生針對受力的分析能力。那么在平衡問題當中,最為常見的問題就是單個物體的平衡和連接體的平衡這兩種形式,而單個物體的平衡主要還包含三個力的平衡、動態平衡以及三個以上的平衡;在連接體的平衡問題當中,就可以合理運用整體法或者是隔離法進行針對這一問題開展分析。
例如:假設面前正在有兩根相同長度的繩子,分別劃分成為AB、BC,這兩根繩子一同進行吊起一個重物,并且促使兩根繩子處于靜止狀態下,而這兩根繩子和水平方向的夾角都是60°,將在確保AB繩子和水平方向夾角不變的基礎之下,從而把BC繩子隨著水平方向進行逐漸改變,那么在這個時候存在的問題就是:BC繩子的拉力變化情況是什么。
針對上述問題,則是就可以合理使用整體法進行解決,從而針對力開展有效的處理。要把AB、BC這兩根繩子都作為一個整體,在運用動態平行四邊形的方法,作出力的平行四邊形,從而就會發現BC繩子拉力變化是屬于先減小后增大的。那么在物理解題的過程當中,就可以合理運用清晰明確的解題思路,有效把作用力和反作用力之間的關系進行結合,最終得到結果,進而提升自身的解題效率。
3.空間想象調動整體思維
空間的想象力在功能和動量關系解題當中占有著重要位置。如,假設一個物體在進行斜向碰撞上下兩個方向從而產生兩個動量變量V1和V2的時候,這就需要合理運用空間想象力,在自身的腦海中進行構建物理模型。
例如:假設當前存有的一個傾角為30°的斜面一直都在停留在粗糙的水平面上方,其質量作為34千克。把質量ma=14千克,mb=2千克的物體a和b進行定滑輪連接,當A在加速度沿斜面進行下滑的時候,是2.5/秒,提問地面針對斜面體的支持力N是多少。
分析:在上述題目當中,有很多都是屬于多個作用力,那么也就是說可以在解題思路中逐漸運用整體思維方式,從而把A、B以及斜面當作是整體,可以通過自己的想象力,想象成為是一個人在進行擔水,而在擔水的過程當中地面針對車的摩擦力就可以轉換成為地面針對人的摩擦力。得出:
在解析的過程當中,主要是把A、B以及斜面當作是整體,在此基礎上進行分析A和B的受力情況,充分調動自身的空間想象力整體思維,從而把A和B這兩種物體的合理和地面支持力聯系成為一個整體的系統,在把實體物體線條化,以此形式分析出物體之間的受力關系[3]。
結束語
綜上所述,在高中物理力學解題過程當中,合理運用整體法不僅能有效減少學生自身的審題時間,還能有效降低解題難度,從而幫助學生更快的進行解決問題,而且運用整體法還能透過現象的本質發現其中所存有的本質和規律,在各個物體之間的受力關系和運動變化中,運用整體法研究、處理和解決問題,進一步促進我國高中物理學科的開展。
參考文獻
[1]楊博睿.議高中物理力學解題中整體法的運用[J].科學大眾(科學教育),2017(2):30-30.
[2]邵嫣然.關于高中物理力學解題中整體法的分析策略[J].科技經濟導刊,2018(5).
[3]劉洪弛.整體法在高中物理力學解題中的運用[J].中學課程輔導(教師通訊),2018(1).

