臺階式蓖齒封嚴特性試驗與數值研究

郭佳男 孫科 張浩 周超

摘要：本文在二維平面蓖齒試驗臺的基礎上，利用試驗研究與數值計算相結合，對臺階蓖齒進行了幾何參數和氣動參數影響下的蓖齒流動特性研究。結果表明，流量系數隨壓比的增大而增大.在低雷諾數范圍，流量系數隨雷諾數的增大而增大，在高雷諾數范圍，流量系數隨雷諾數增大基本不變。齒數研究中，隨著齒數增多，流量系數減小。齒頂間隙研究中，隨著齒頂間隙的增大，流量系數減小。

關鍵詞：封嚴蓖齒，幾何參數;氣動參數，流動特性，流量系數

中圖分類號;V233;文獻標識碼：A

封嚴裝置是燃氣渦輪發動機空氣系統必不可少的元件，蓖齒封嚴是最為常見的一種，這種封嚴結構可靠，有很好的封嚴特性[1～3]。隨著航空發動機性能、轉速的不斷提高，以及發動機循環參數（壓力、溫度）的增高，封嚴技術已成為影響發動機機性能和使用壽命的重要因素[4，5]。利用蓖齒尖與封嚴環面之間的間隙節流和齒腔中渦流來增加流阻，達到到減少泄漏的目的[6]。

國內學者劉有軍通過有限元數值計算方法，采用流體力學中耗散函數分析蓖齒空腔的耗散特性[7]。而紀國劍[8]的研究表明，低轉速對臺階蓖齒泄漏影響相對較小。由于旋轉狀態下試驗測量難度大，周期長，為了提高試驗效率，獲取更為準確的試驗數據，本文在靜止蓖齒試驗臺上，基于某型發動機真實的臺階式蓖齒，通過試驗和數值計算分析了實際應用中不同幾何和氣動參數對于蓖齒泄漏流量和流量系數的影響，并對蓖齒流動機理進行了深入研究。其中幾何參數包括齒數和齒頂間隙，氣動參數包括壓比和雷諾數。

1 研究模型

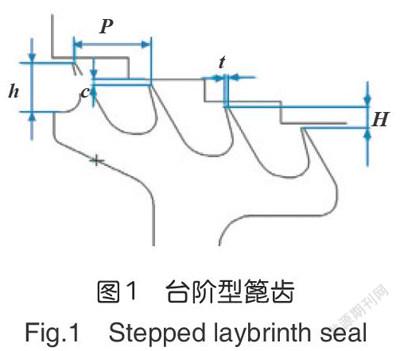
研究模型為臺階型蓖齒，結構示意圖如圖1所示，其中，齒數N為4，臺階高度H為2mm，齒間距P為7mm，齒高度h為4.5mm，齒頂厚度t為0.25mm。

2 試驗裝工和試驗方法

2.1 試驗裝置和測t方法

本文試驗系統示意圖如圖2所示，主要包括壓氣機、儲氣罐、手動調節和電動調節閥、試驗段和測量系統。壓氣機可以提供最大壓力0.8MPa、最大流量1kg/s的氣體。調節閥用來調節壓力，測量系統包括壓力、溫度以及質量流量的測量。壓力和溫度測量方式為上蓋板打孔測量，質量流量測量采用在試驗段下游通過孔板流量計測量。試驗過程中，氣體從壓氣機流入試驗管路，經過一系列的調節閥調節到合適的壓力進入試驗段，在試驗段通過測量系統測得壓力和質量流量，最后通過試驗段下游的孔板流量計排入大氣。測量系統的信號全部由采集系統送入計算機顯示。圖

3 為試驗臺實物圖。

2.2 參數定義

2.2.1 齒頂間隙

在封嚴蓖齒中，齒頂間隙為齒頂距離上壁面的距離，如圖4所示[9]。

2.2.2 壓比

蓖齒進出口壓比定義為：式中：p⁰是進口總壓;p₁是出口總壓;壓比是蓖齒進口總壓與出口總壓之比。

2.2.3 理想流量式中：p_t，0，T_t，0和p₁分別為進口總壓、總溫和出口靜壓，R和κ分別為氣體常數和絕熱指數。A為蓖齒頂距離頂端的流通面積[10]。

2.2.4 流量系數式中：C_D為流量系數;m為實際流量;m_id為理想流量。由于蓖齒不同幾何參數下流量差異較大，故選用了無量綱化的流量系數這一變量來表征封嚴特性。

2.2.5 流動雷諾數式中：ρ為氣流密度;v_x為軸向速度;d為當量直徑;μ為氣流的[動力]黏度;c為齒頂間隙;L為平壁模型寬度。

3 試驗結果與分析

3.1 壓比的影響

圖5為流量和流量系數隨壓比變化的曲線圖，圖中5條曲線分別對應不同的雷諾數，雷諾數從大到小到小依關系是Re_max>Re₄>Re₃>Re₂>Re₁。由圖5（a）可以看出，隨著壓比的增大，流量增大，變化規律基本呈線勝變化，并月增大斜率逐漸降低。由圖5（b）可以看出同時不同雷諾數下的流量系數最大偏差約4%，隨著壓比增大，各雷諾數下流量系數趨于一致。

3.2 雷諾數的影響

圖6為同一齒頂間隙下流量和流量系數隨雷諾數變化的曲線。由圖6（a）中可以看出，隨著流動雷諾數的增大，質量流量呈線性增大，不同壓比下流量增長的斜率一致;由圖6（b）中可以看出在低雷諾數范圍，流量系數隨雷諾數的增大而增大;這是由于在低雷諾數范圍，邊界層較厚，黏性力相對較大，雷諾數變大時摩擦損失減小，流量系數隨之增大。在高雷諾數范圍（Re>10000），流量系數隨雷諾數增大而變化很小;這是由于在高雷諾數范圍，邊界層較薄且變化很小，相對于流通慣性力，黏性力很小，這時流量系數的變化主要取決于蓖齒進出口壓降和齒尖有效流通面積。高雷諾數下型面阻力和黏性阻力組成的總阻力中，黏性阻力比重較小，這也說明阻力對尺寸大小不敏感，相當于進入自模化區，可以采用放大模型對蓖齒進行試驗研究。

3.3 齒數的影響

圖7為同一齒頂間隙不同壓比下流量和流量系數隨齒數變化的曲線圖。由圖7（a）中可以看出，隨著齒數增多，流量降低，流量降低幅度逐漸降低。并且隨著壓比增大，不同齒數影響下流量的差距逐漸增大;由圖7（b）中可以看出，流量系數隨壓比增大而增大，五齒比二齒的流量系數降低約60%。相同壓比下，齒數越多，流量系數越小。齒數增多，節流損失增大，另外由于齒數的增加，齒腔的數目就會增加，齒腔數目的增加實際上就造成了泄漏出去的氣體的渦流阻力和沿程阻力明顯增大，流程明顯增長，因而產生的泄漏量就相對較小。

3.4 齒頂間隙的影響

由圖8（a）中可以看出，在相同壓比下，隨著齒頂間隙增大，流量接近線性增大;由圖8（b）中可以看出，在壓比一定的情況下，流量系數隨間隙的增大逐漸減小，并且減小的斜率逐漸降低，這是由于臺階對氣體的阻擋作用明顯，質量流量雖然增大，但是相對理想流量增大的幅度較小，所以流量系數反而減小，流量系數從齒頂間隙1.0mm到齒頂間隙0.15mm降低約20%。在下面的數值計算中通過流場圖有較為詳細的分析。

4 數值分析

為了對試驗結果進行進一步分析，通過數值計算獲得了蓖齒腔內的流場云圖，可清晰地看出流場的流動情況，進而對蓖齒封嚴進行機理研究。

4.1 計算模型及計算方法

將計算域劃分為多個子區域，分塊進行網格的劃分，如圖9所示。蓖齒附近采用非結構化網格，其他位置采用結構化網格，在齒尖等速度梯度變化比較大的地方進行網格加密，保證疏密網格之間過渡的均勻性。上壁面和下壁面都要劃分邊界層網格，邊界層共8層，Yplus在11的量級，網格總數在24萬左右。

本文用商業軟件Fluent6.3進行求解，選擇二維穩態模型，方程求解采用分離隱式求解器和SIMPLE算法，離散格式為二階迎風格式。湍流模型采用Realizable k-ε模型。采用增強壁面處理方法來解決近壁區域附近的流動問題。上下固體壁面為無滑移和絕熱邊界條件，靜止壁面。流體為理想氣體，物性參數隨溫度變化，考慮黏性隨溫度變化，計算時采用sutherland公式。

進口條件為壓力進口，給定進口總壓和總溫;出口條件為壓力出口，給定出口靜壓。

4.2 網格無關性驗證

為了消除網格疏密程度對于計算結果的影響，對齒數N=4，齒頂間隙c=0.5mm的同一蓖齒模型進行不向數目的網格劃分，其網格總數目為16萬、20萬、24萬左右。圖10為網格數量分別為16萬、20萬和24萬三套網格下的數值計算結果。

由計算結果得出，在同一工況下，三種網格計算結果統計出的質量流量偏差都在0.5%以內。由圖可知，網格疏密對于質量流量隨壓比的變化規律也沒有影響。由此可見當網格數達到一定程度后，即網格數量達到24萬以上，網格疏密程度對于計算結果的影響可以忽略，本文網格總數選擇24萬。

4.3 計算結果與試驗結果對比

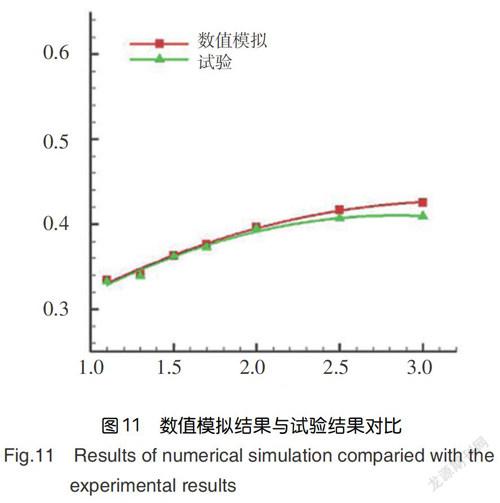
圖11為流量系數隨壓比的變化曲線，并將試驗結果和計算結果進行對比。從圖中可以，試驗結果與計算結果隨壓比的變化趨勢一致，即隨壓比的逐漸增大，流量系數逐漸增大，且增長的斜率越來越小。計算數據略大于試驗數據，兩者的最大偏差為2.8%。這可能是由于壓比增大時，數值計算中湍流模型帶來的偏差逐漸增大導致的。計算與試驗整體偏差相對較小，符合較好，可用來分析蓖齒腔內流場流動機理。

4.4 計算結果分析

4.4.1 壓比的影響

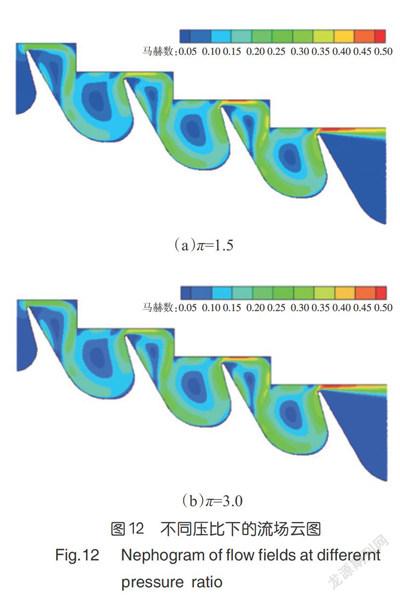
由圖12可得，壓比為3.0時氣流的馬赫數較壓比為1.5時大，相應的可壓縮性變大，氣流更容易流過齒頂間隙，流量系數增大。

4.4.2 雷諾數的影響

由圖13可以看出，低雷諾數下，邊界層較厚，黏性力相對較大，雷諾數變大時摩擦損失減小，流量系數因而隨之增大，在雷諾數較高時，邊界層較薄且變化很小，相對于流通慣性力，黏性力很小，這時流量系數的變化主要取決于蓖齒進出口壓降和齒尖有效流通面積，因而流量系數變化不大。

4.4.3 齒頂間隙的影響

從圖14的速度場中可以看出，齒頂間隙c=1.Oxnm時的氣流速度明顯大于c=0.25mm時的氣流速度，而且經臺階的阻擋后，高速氣流直接進入渦流區，這樣就會使得c=1.0mm時的渦流損失和高速氣流拐彎損失較大，使其流量系數較小。另外，在c=0.25mm時，臺階處距離齒頂節流處的相對距離較遠，使得節流后的氣流在撞擊臺階面之前已經部分散開，由臺階造成的損失減小。

5 結論

通過分析，可以得出以下結論：

（1）隨著壓比的增大，流量和流量系數均增大，但增大幅度減小。在低雷諾數范圍，流量系數隨雷諾數的增大而增大，在高雷諾數范圍，流量系數隨雷諾數增大而變化很小，表明黏性阻力影響較小。因此，在高雷諾數范圍內，可考慮采用放大模型進行更加深人試驗的研究。

（2）研究范圍內，齒數和齒頂間隙對蓖齒流量系數影響較大。壓比一定時，隨著齒數的增加，流量系數減小;齒頂間隙和齒數一定時，隨著齒頂間隙的增大，臺階齒的流量系數減小。

（3）數值計算對試驗結果進行了驗證，對比結果符合良好。數值模擬還揭示了蓖齒腔內的流動圖譜，經過對流場的分析研究發現，造成蓖齒流動損失的主要原因是齒尖節流以及蓖齒腔內的渦流。

參考文獻

[1]《航空發動機設計手冊》總編委會.航空發動機手冊：傳動及潤滑系統[M].北京：航空工業出版社，2002.

[2]Bruce M，Steinetz，Robert C，et al.Engine seal technologyrequirements to meet Nasa's advanced subsonic technologyprogram goals[R].AIAA-94-2698，1994.

[3]Saikishan S，Gerald L M.Analysis of flow parametersinfluencing carry-over coefficient of labyrinth seals[R].ASMEGT2009-59245，2009.

[4]李志剛，李軍，豐鎮平.蜂窩密封流動特性的數值研究和泄漏量計算公式的構造[J].機械工程學報，2011，47（2）：142-148.

[5]紀國劍.航空發動機典型蓖齒封嚴泄漏特性的數值和試驗研究[D].南京：南京航空航天大學，2008.

[6]賈惟.封嚴腔幾何結構對渦輪性能影響的數值研究[J].科學技術與工程，2018，18（06）：177-183.

[7]劉有軍.鋸齒型徑向迷宮密封機理研究[J].潤滑與密封，2002（6）：20-21

[8]紀國劍，吉洪湖.臺階蓖齒與襯套軸向位置和轉速對封嚴特性影響的試驗[J].航空動力學報，2008，23（3）：421-424.

[9]Egli A.The leakage of gases through narrow channels[J].TransofASME，1935，37：63-67.

[10]Martin H M.Labyrinth Packing[R].Engineering，1908，35-36.