基于支持向量機的注漿錨桿錨固參數反分析

孫長寧 蘇立君 朱秦 李丞

摘要：注漿錨桿極限抗拔力一般通過現場試驗進行測定，但在錨固工程數值模擬分析過程中，所需的錨固參數（如注漿體的黏結強度和摩擦角）很難直接確定。提出了一種基于支持向量機的注漿錨桿錨固參數反分析方法，即利用錨桿極限抗拔力反分析錨固參數。選取錨桿極限抗拔力作為實測目標，結合均勻試驗和支持向量機建立錨固參數與實測目標之間的映射關系，通過蒙特卡洛法枚舉大量錨固參數樣本，利用上述已建立的映射關系計算枚舉的錨固參數樣本，得到對應目標的計算值。在此基礎上，根據目標實測值篩分得到符合條件的目標計算值對應的錨固參數，并通過關于注漿錨桿的模型案例說明了該方法的可行性。

關鍵詞：注漿錨桿;錨固參數;支持向量機;反分析：極限抗拔力

中圖分類號：U456.3

文獻標志碼：A

doi：10. 3969/j .issn. 1000- 13 79.2019.01. 032

目前，注漿錨桿被廣泛應用于邊坡、隧道工程中，其最重要的參數為極限抗拔力，一般通過現場試驗確定。許多學者對注漿錨桿的極限抗拔力進行了理論研究。Li等[1]根據錨桿拉拔試驗，提出了拉拔荷載作用下注漿錨桿的力學分析模型：Cai等[2]考慮到錨桿與巖體變形協調，建立了注漿巖石錨桿的軸力預測理論模型，Shahin等[3]采用神經網絡方法預測了錨桿的極限抗拔承載力：魏新江等[4]考慮錨桿注漿體界面強度和注漿體巖土體界面強度對全長黏結式錨桿抗拔力的影響，以及漿體與巖土界面的塑性區發展，推導得出了全長黏結式錨桿的抗拔力計算公式：鄧宗偉等[5]基于統一強度理論和極限平衡原理，結合預應力錨索破裂面的形狀，推導出了預應力錨索極限抗拔承載力的計算公式：賀建清等[6]基于改進的Mohr - Coulomb強度準則，從塑性力學極限分析上限定理出發，利用虛功原理推導得出了巖石錨桿極限抗拔承載力的計算公式。然而，在注漿錨桿錨固工程數值分析中，需要提前確定相關錨固參數（如單位長度上注漿體的剛度、黏結強度和摩擦角等），而不是極限抗拔力[7]，但關于注漿錨桿錨固參數的研究相對較少。John等8]給出了一些關于上述注漿錨桿錨固參數的經驗公式，但沒有給出注漿體摩擦角的近似公式：Li等[9]基于注漿錨桿的極限抗拔力，利用二分法對注漿巖石錨桿的錨固參數進行了反分析，但該方法需要事先確定參數初值，其對錨固參數最終分析結果影響較大。

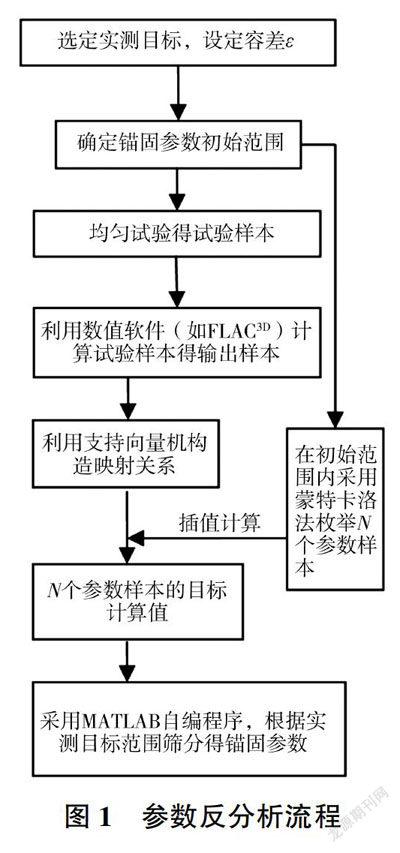
針對上述問題，本文提出了一種基于支持向量機的注漿錨桿錨固參數反分析方法，即利用錨桿極限抗拔力反分析錨固參數。選取錨桿極限抗拔力作為實測目標，結合均勻試驗和支持向量機建立錨固參數與實測目標之間的映射關系，通過蒙特卡洛法枚舉大量錨固參數樣本，利用上述映射關系計算錨固參數樣本，得到對應實測目標的計算值，并根據目標實測值，篩分得到符合條件的目標計算值對應的錨固參數。

1 基于支持向量機的注漿錨桿錨固參數反分析

2 算例分析

為了證明本文方法的可行性，選用文獻[7]中的注漿巖石錨桿拉拔試驗案例，根據錨桿極限抗拔力，利用該方法反分析注漿錨桿的錨固參數。所選案例的FLAC3D數值模型尺寸為0.4 mx0.7 mx0.4 m.模型內部設置0.5 m長的錨桿，其余單元為巖體，模型邊界圍壓為2 MPa。巖體與錨桿的相關參數見表1。

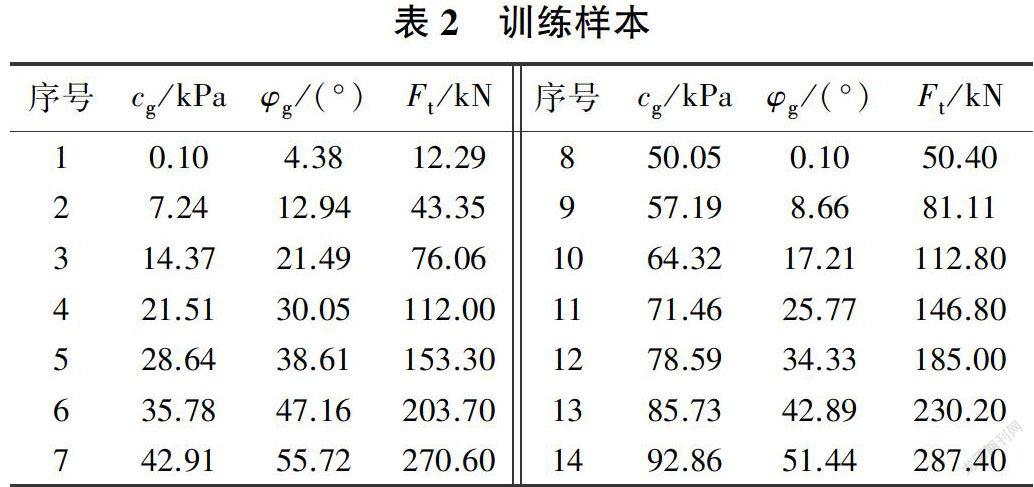
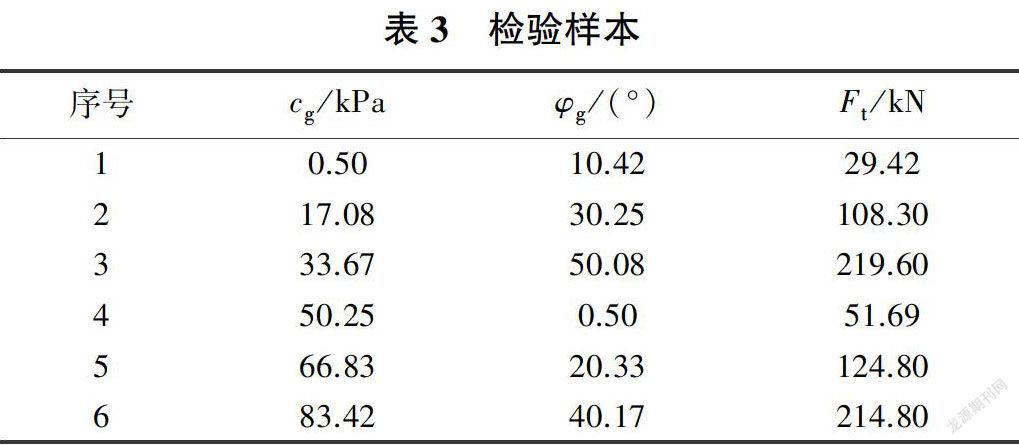
選擇錨桿的極限抗拔力作為實測目標，將注漿體黏結強度（c）和摩擦角（φ）作為待定錨固參數。根據試算或現有資料，確定錨固參數初始范圍：c為[0，100 kPa]，φ為[0，50°]，將上述兩個參數作為隨機參數。針對上述隨機參數，將其分為14個水平，即2個參數14個水平，采用MATLAB自編程序得到均勻表U14（142），從而得到14組參數的輸入樣本。根據上述FLAC3D軟件建立的力學模型，計算輸入樣本進而得到對應的輸出樣本（即錨桿的極限抗拔力），見表2。重復上述步驟，獲得6組檢驗樣本，見表3。

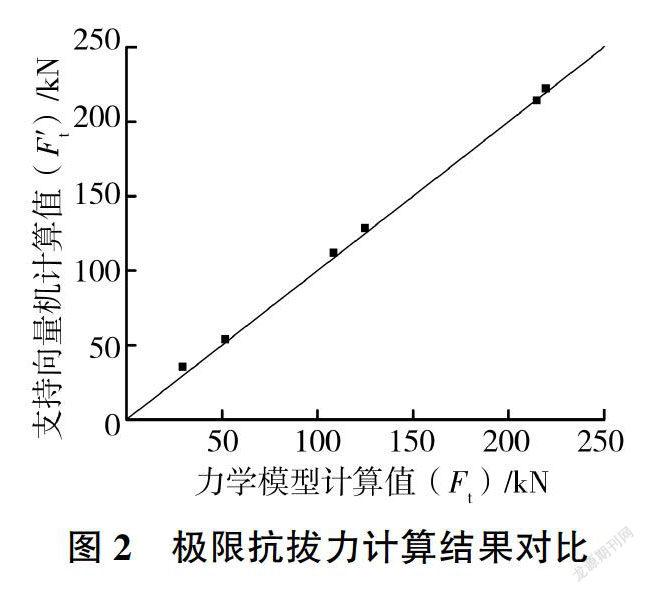
根據表2中的訓練樣本，采用支持向量機建立注漿體黏結強度、摩擦角與錨桿極限抗拔力之間的映射關系，均方根誤差小于0.001。利用上述已建立的映射關系計算表3中檢驗樣本的6組參數，得到對應的極限抗拔力預測值，與表3中力學模型計算得到的極限抗拔力結果進行對比，見圖2。由圖2可以看出，兩種方法得到的結果接近，因此上述基于支持向量機建立的映射關系是有效且可用的。

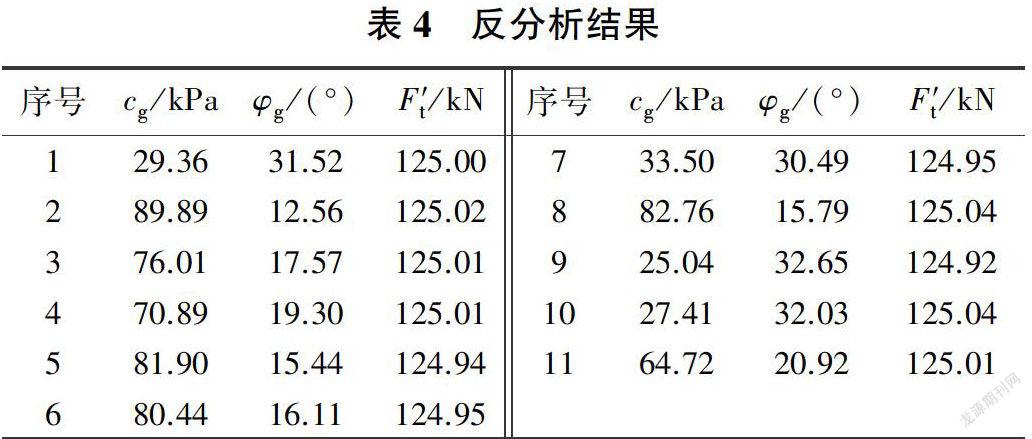
設注漿錨桿極限抗拔力的現場試驗實測值為125kN，允許容差ε=0.1 kN，則目標實測值為[124.9，125.1]。根據待定錨固參數的初始范圍，利用蒙特卡洛法枚舉10 000組隨機樣本，采用上述已建立的映射關系計算每組隨機樣本，進而得到對應的10 000組輸出樣本，即錨桿極限抗拔力計算值。在此基礎上，結合目標實測值范圍，篩分出該范圍內的目標計算值以及對應的錨固參數，見表4。

由表4可知，反分析結果不是唯一解，而是兩個錨固參數的多種組合，主要原因是目標函數為1個方程、2個未知數，從數學求解的角度看，其結果為多組解。表4反分析結果不一定是注漿體的真實錨固參數，但每一組解均滿足錨桿極限抗拔力的計算值等于現場實測值，因此可以替代真實錨固參數，解決數值模擬過程中錨固參數取值的問題。

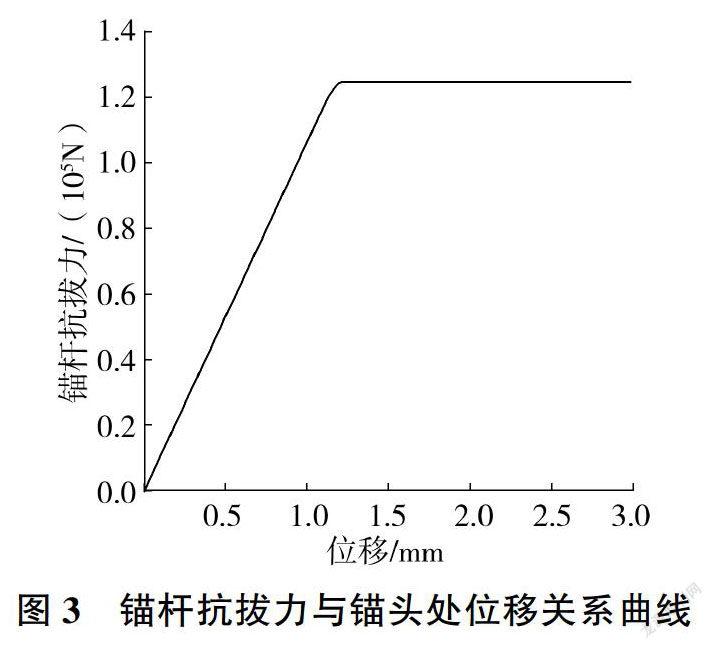
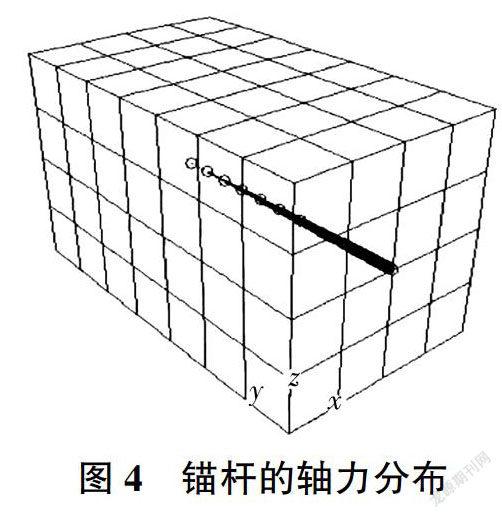
根據現有資料和參數的物理意義可知，注漿體的錨固參數φ約為30°[9]。根據表4，當錨固參數取c=29.36 kPa.φ=31.52°時，將其輸入到上述用FLAC3D建立的數值模型中進行分析，結果見圖3和圖4。由圖3可知，錨桿抗拔力隨錨頭處位移的增大而增大，當錨頭處位移增大到一定程度時，錨桿抗拔力達到最大值，并且趨于平穩，此時即為錨桿的極限抗拔力。由圖4可知，注漿錨桿距離錨頭越近，軸力越大;注漿錨桿距離錨頭越遠，軸力越小。

3 結語

提出了一種基于支持向量機的注漿錨桿錨固參數反分析方法。利用該方法可以根據錨桿的極限抗拔力試驗值反分析注漿體的錨固參數，從而便于注漿錨桿加固工程數值模擬過程中錨固參數的確定。同時，通過一個簡單案例說明了該方法的可行性。通過引入支持向量機智能算法，建立樣本之間的映射關系，進而快速計算大量參數樣本，提高了參數反分析的效率。提出的參數反分析流程具有通用性。針對其他具體工程的參數反分析問題，建立相應的力學模型，選擇合適的實測目標（如位移）和待定參數（如土體抗剪強度指標），也可利用上述流程進行參數反分析。

參考文獻：

[1] L1 C，STILLBORG B.Analytical Models for Rock Bolts[ J].Intemational Journal of Rock Mechanics and MiningSciences， 1999， 36（8）：1013-1029.

[2]

CAI Y，ESAKI T，JIANG Y.An Analytical Model to PredictAxial Load in Grouted Rock Bolt for Soft Rock Tunnelling[J]. Tunnelling and Underground Space Technology， 2004，19（6）：607-618.

[3] SHAHIN M A， JAKSA M B.Neural Network Prediction ofPullout Capacity of Marquee Cround Anchors[J].Computersand Geotechnics， 2005， 32（3）： 153-163.

[4]魏新江，張世民，危偉，全長粘結式錨桿抗拔力計算公式的探討[J].巖土工程學報，2006，28（7）：902-905.

[5]鄧宗偉，冷伍明，李志勇，等，基于統一強度準則的預應力錨索極限承載力計算[J].巖石力學與工程學報，2007，26（6）：1138-1144.

[6] 賀建清，肖蘭，張文勇，等，基于改進的Mohr- Coulomb強度準則下巖石錨桿極限抗拔承載力計算[J].巖土力學，2016，37（9）：2484-2488.

[7] Itasca Consulting Group， Ir'ic. FLAC3D： Fast Lagran～;ian A—nalysis of Continua in 3 Diruensions[M].Minneapolis： MN，2006： 95-108.

[8] JOHN C M， VAN DILLEN D E.Rockbolts：a NewNumerical Representation and Its Application in Tunnel De-sign[ C]//The 24th US Symposium On Rock Mechanics（USRMS）. Texas： American Rock Mechanics Association，1983： 66-76.

[9] LI Bin， TAIYUE Q， WANG Z，et al.Back Analysis ofGrouted Rock Bolt Pullout Strength Parameters from FieldTests[J].Tunnelling and Underground Space Technology，2012， 28： 345-349.

[10] 方開泰，均勻設計及其應用（Ⅱ）[J].數理統計與管理，1994，13（3）：52-55.

[11] SONG Zhigang， SONG Jie. Reliability Analysis of CompartmentFire by Improved Response Sruface Method[C]//Proceedings ofthe Eleventh International Symposium on Structural Engjneering.Beijing： Science Press，2010： 1271-1276.

[12]趙洪波，馮夏庭，位移反分析的進化支持向量機研究[J].巖石力學與工程學報，2003，22（ 10）：1618-1622.

[13] 許傳華，任青文，周慶華，基于支持向量機和模擬退火算法的位移反分析[J].巖石力學與工程學報，2005， 24 （22）：4134-4138.

[14] 許傳華，任青文，鄭治，等，索風營水電站地下洞室巖體力學參數的位移反分析[J].巖土工程學報，2006， 28 （11）：1981-1985.

[15] 李波，徐寶松，武金坤，等，基于最小二乘支持向量機的大壩力學參數反演[J].巖土工程學報，2008， 30（11）： 1722-1725.