凸透鏡成像規律的代數研究

王祉鑒

我記得初二剛學凸透鏡成像時，我們班的一位同學告訴我，她在課外習題中看到這么一個結論，說凸透鏡成實像時，物距與像距的倒數和等于焦距的倒數（即 ）.我當時就試圖過去證明這個結論，但發現無從下手.我就暫且將它放在了一邊.

到初三后，進行第一輪復習.當復習到凸透鏡成像規律這一塊時，我又想起了這個問題.我決定證明它.

本著從特殊到一般的思想，我決定將物體在凸透鏡的兩倍焦點上時成倒立等大的實像這個特殊的成像規律代入式子驗證一下，發現：當 時，

滿足 的結論.

但這畢竟是特殊情況，不具有普遍性.所以我開始研究一般情況下物距、像距和焦距是否滿足這個式子.然而，我仍然沒有什么思路。

有一次，我在閱讀數學讀物時，看到這么一句話，說數學是解決自然科學問題的關鍵.我感到非常贊同.我想，我為什么不從數學的角度去看待這個問題呢？

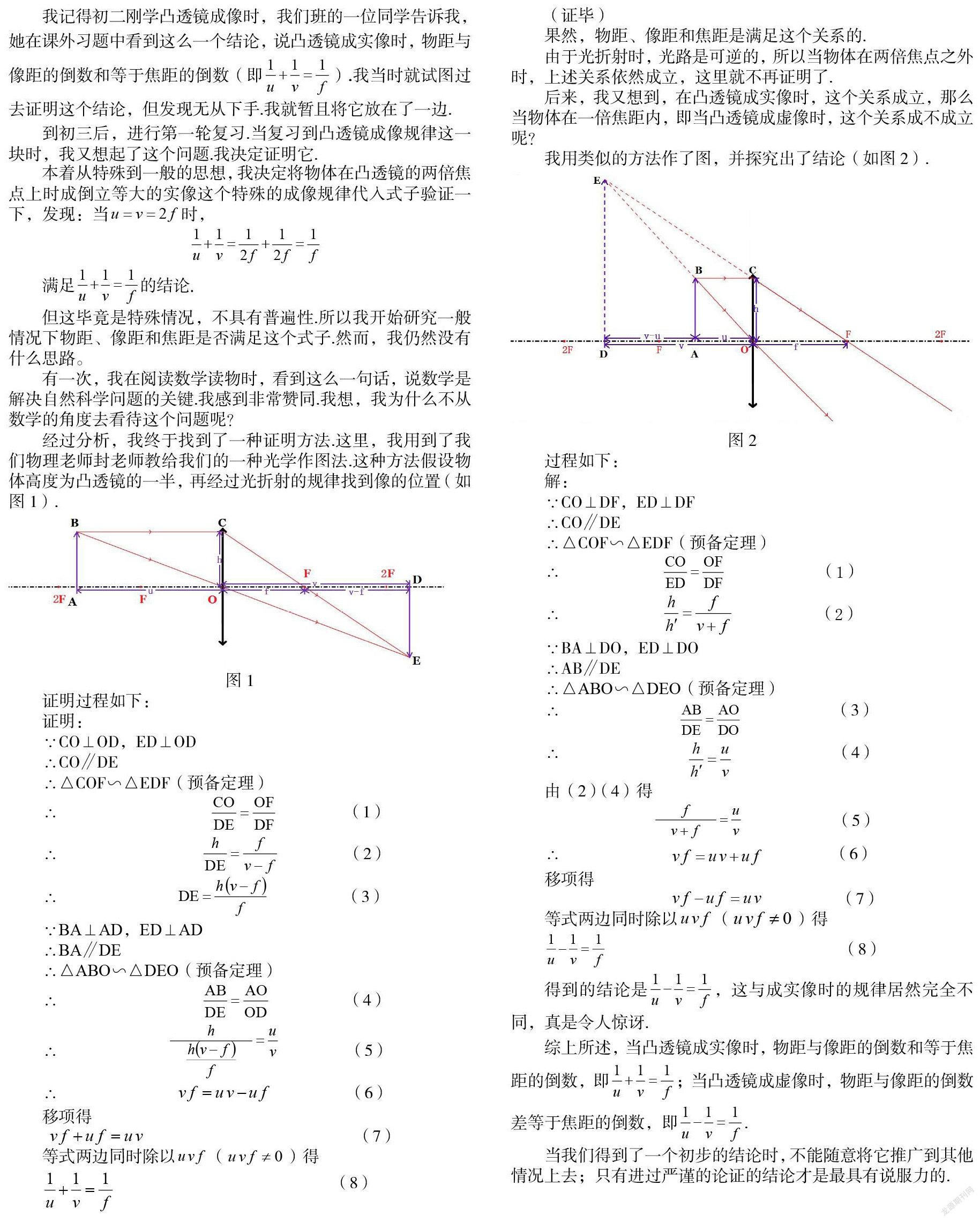
經過分析，我終于找到了一種證明方法.這里，我用到了我們物理老師封老師教給我們的一種光學作圖法.這種方法假設物體高度為凸透鏡的一半，再經過光折射的規律找到像的位置（如圖1）.

果然，物距、像距和焦距是滿足這個關系的.

由于光折射時，光路是可逆的，所以當物體在兩倍焦點之外時，上述關系依然成立，這里就不再證明了.

后來，我又想到，在凸透鏡成實像時，這個關系成立，那么當物體在一倍焦距內，即當凸透鏡成虛像時，這個關系成不成立呢？

我用類似的方法作了圖，并探究出了結論（如圖2）.

得到的結論是 ，這與成實像時的規律居然完全不同，真是令人驚訝.

綜上所述，當凸透鏡成實像時，物距與像距的倒數和等于焦距的倒數，即 ;當凸透鏡成虛像時，物距與像距的倒數差等于焦距的倒數，即 .

當我們得到了一個初步的結論時，不能隨意將它推廣到其他情況上去;只有進過嚴謹的論證的結論才是最具有說服力的.