從二次函數到一元二次方程

徐章韜

摘要：函數與方程兩部分內容的知識結構是一致的：數學建模與數學對象性質的研究，從外部世界到數學內部世界，再到外部世界，體現數學的來源與目的。從教學的角度看，既可以從一元二次方程講到二次函數，也可以從二次函數講到一元二次方程。由此，還可以串聯很多相關知識，從而理解教材思路，感悟數學思想。得到的教學啟示是：精致練習是必要的，但不一定是充分的;思想、方法和觀點要化成有層次的引導性問題，讓學生在訓練中更好地掌握。

關鍵詞：教育數學二次函數一元二次方程數學建模知識結構

函數與方程是數學的兩大主題，也是中學數學的重點和難點內容。兩者的知識結構是一致的：數學建模與數學對象性質的研究，從外部世界到數學內部世界，再到外部世界，體現數學的來源與目的。從教學的角度看，既可以從一元二次方程講到二次函數，也可以從二次函數講到一元二次方程。這是兩種互補的角度。由此，還可以串聯很多相關知識，從而理解教材思路，感悟數學思想。

一、數學建模

數學建模搭建了數學與外部世界的聯系，也是數學產生的動力。一元二次方程和二次函數都是數學建模的產物。這兩部分內容都是落實數學建模核心素養的重要載體。具體的解方程、研究函數性質則是數學建模過程中的副產品。

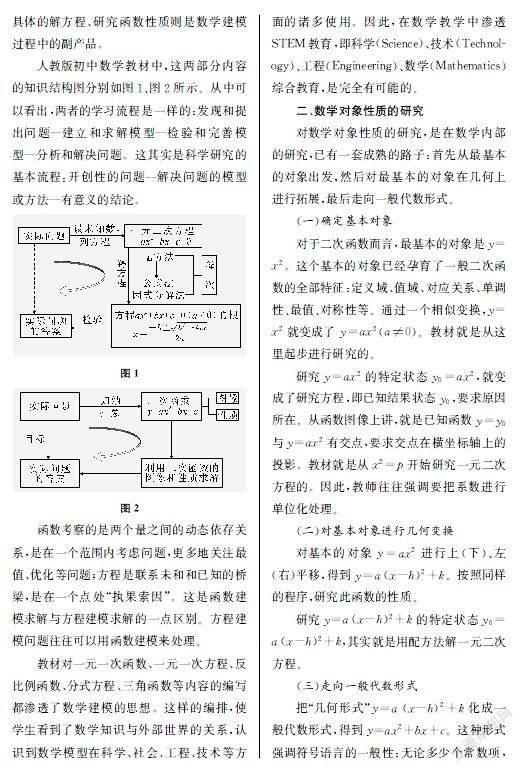
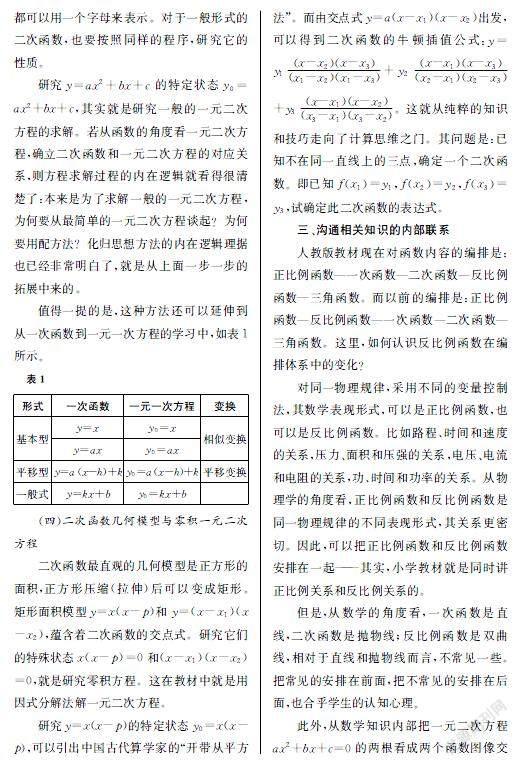
人教版初中數學教材中，這兩部分內容的知識結構圖分別如圖1、圖2所示。從中可以看出，兩者的學習流程是一樣的：發現和提出問題—建立和求解模型—檢驗和完善模型—分析和解決問題。這其實是科學研究的基本流程：開創性的問題—解決問題的模型或方法—有意義的結論。

函數考察的是兩個量之間的動態依存關系，是在一個范圍內考慮問題，更多地關注最值、優化等問題;方程是聯系未和和已知的橋梁，是在一個點處“執果索因”。這是函數建模求解與方程建模求解的一點區別。方程建模問題往往可以用函數建模來處理。

教材對一元一次函數、一元一次方程、反比例函數、分式方程、三角函數等內容的編寫都滲透了數學建模的思想。這樣的編排，使學生看到了數學知識與外部世界的關系，認識到數學模型在科學、社會、工程、技術等方面的諸多使用。因此，在數學教學中滲透STEM教育，即科學（Science）、技術（Technology）、工程（Engineering）、數學（Mathematics）綜合教育，是完全有可能的。

二、數學對象性質的研究

對數學對象性質的研究，是在數學內部的研究，已有一套成熟的路子：首先從最基本的對象出發，然后對最基本的對象在幾何上進行拓展，最后走向一般代數形式。

（一）確定基本對象

對于二次函數而言，最基本的對象是y=x2。這個基本的對象已經孕育了一般二次函數的全部特征：定義域、值域、對應關系、單調性、最值、對稱性等。通過一個相似變換，y=x2就變成了y=ax2（a≠0）。教材就是從這里起步進行研究的。

研究y=ax2的特定狀態y0=ax2，就變成了研究方程，即已知結果狀態y0，要求原因所在。從函數圖像上講，就是已知函數y=y0與y=ax2有交點，要求交點在橫坐標軸上的投影。教材就是從x2=p開始研究一元二次方程的。因此，教師往往強調要把系數進行單位化處理。

（二）對基本對象進行幾何變換

對基本的對象y=ax2進行上（下）、左（右）平移，得到y=a（x-h）2+k。按照同樣的程序，研究此函數的性質。

研究y=a（x-h）2+k的特定狀態y0=a（x-h）2+k，其實就是用配方法解一元二次方程。

（三）走向一般代數形式

把“幾何形式”y=a（x-h）2+k化成一般代數形式，得到y=ax2+bx+c。這種形式強調符號語言的一般性：無論多少個常數項，都可以用一個字母來表示。對于一般形式的二次函數，也要按照同樣的程序，研究它的性質。

研究y=ax2+bx+c的特定狀態y0=ax2+bx+c，其實就是研究一般的一元二次方程的求解。若從函數的角度看一元二次方程，確立二次函數和一元二次方程的對應關系，則方程求解過程的內在邏輯就看得很清楚了：本來是為了求解一般的一元二次方程，為何要從最簡單的一元二次方程談起？為何要用配方法？化歸思想方法的內在邏輯理據也已經非常明白了，就是從上面一步一步的拓展中來的。

值得一提的是，這種方法還可以延伸到從一次函數到一元一次方程的學習中，如表1所示。

形式一次函數一元一次方程變換基本型y=xy0=xy=axy0=ax相似變換平移型y=a（x-h）+ky0=a（x-h）+k平移變換一般式y=kx+by0=kx+b（四）二次函數幾何模型與零積一元二次方程

二次函數最直觀的幾何模型是正方形的面積，正方形壓縮（拉伸）后可以變成矩形。矩形面積模型y=x（x-p）和y=（x-x1）（x-x2），蘊含著二次函數的交點式。研究它們的特殊狀態x（x-p）=0和（x-x1）（x-x2）=0，就是研究零積方程。這在教材中就是用因式分解法解一元二次方程。

研究y=x（x-p）的特定狀態y0=x（x-p），可以引出中國古代算學家的“開帶從平方法”。而由交點式y=a（x-x1）（x-x2）出發，可以得到二次函數的牛頓插值公式：y=y1（x-x2）（x-x3）（x1-x2）（x1-x3）+y2（x-x1）（x-x3）（x2-x1）（x2-x3）+y3（x-x1）（x-x2）（x3-x1）（x3-x2）。這就從純粹的知識和技巧走向了計算思維之門。其問題是：已知不在同一直線上的三點，確定一個二次函數。即已知f（x1）=y1，f（x2）=y2，f（x3）=y3，試確定此二次函數的表達式。

三、溝通相關知識的內部聯系

人教版教材現在對函數內容的編排是：正比例函數—一次函數—二次函數—反比例函數—三角函數。而以前的編排是：正比例函數—反比例函數—一次函數—二次函數—三角函數。這里，如何認識反比例函數在編排體系中的變化？

對同一物理規律，采用不同的變量控制法，其數學表現形式，可以是正比例函數，也可以是反比例函數。比如路程、時間和速度的關系，壓力、面積和壓強的關系，電壓、電流和電阻的關系，功、時間和功率的關系。從物理學的角度看，正比例函數和反比例函數是同一物理規律的不同表現形式，其關系更密切。因此，可以把正比例函數和反比例函數安排在一起——其實，小學教材就是同時講正比例關系和反比例關系的。

但是，從數學的角度看，一次函數是直線，二次函數是拋物線;反比例函數是雙曲線，相對于直線和拋物線而言，不常見一些。把常見的安排在前面，把不常見的安排在后面，也合乎學生的認知心理。

此外，從數學知識內部把一元二次方程ax2+bx+c=0的兩根看成兩個函數圖像交點的橫坐標，變形就有ax+b=-cx，這樣左邊是直線，右邊就是雙曲線。即從函數的角度看一元二次方程，可以得到反比例函數，這樣能使反比例函數很容易進入教學。而且，再變一下形，還有ax+cx=-b，就得到了我們熟悉的“雙勾函數”。

事實上，教材從小學階段起就在滲透函數思想以及函數和方程的轉化。比如，在圓的周長公式中滲透的是正比例函數，在矩形的面積公式中滲透的是二元函數，在梯形的面積公式中滲透的是三元函數，在圓的面積公式中滲透的是二次函數。而方程本質上是函數的逆運算：尋求使函數值符合一定要求的自變量就是解方程。函數思想和方程方法是一個事物的兩面，貫穿于數學的所有領域。

四、教學啟示

作為完整的數學教學，既要注重數學與外部世界的聯系，也要注重數學內部之間的關聯。在現實背景下，數學教學更多地在關注數學內部之間的關聯，較少關注數學與外部世界的聯系。但是，即使是關注數學內部之間的關聯，數學教學也需要從理論上提高認識。

（一）精致練習是必要的，但不一定是充分的

根據理性思維的調控特征理論（Adaptive Character of ThoughtRational），知識、技能都需要通過艱苦的學習而獲得和鞏固。精致練習、變式學習是熟能生巧、走向理解、走向遷移的必要條件之一。這一點在現實的課堂教學中，已經運用得相當嫻熟了，學生往往經歷了大量的訓練，也取得了一定的效果。但是，若執著于此，只會把學生引向茫茫題海。人工智能機器是“舉十反一”，通過訓練集逐步習得模式，但是學生不是機器，不能過量采取這種“舉十反一”的做法，還需要能夠對已學習的內容做多角度的解讀。教育數學在這方面的工作是開創性的，強調前后知識之間的“一線串”，強調知識的“前瞻”與“后顧”，讓學生越學越簡單。

（二）思想、方法和觀點要化成有層次的引導性問題，讓學生在訓練中更好地掌握

教材內容往往蘊含著一些原則性的思考方法。這些方法要化為學生的技能，進入學生的頭腦，需要一些精心編制的習題，讓學生能“舉一反三”（人還是比人工智能機器高明的）。好的習題往往凝聚了命題者對課程內容、學生學習基礎的理解。這就是現在理論界正在討論的核心素養如何考的問題。精致練習講究思維的細密性、一步一個臺階，而有層次的引導性問題則強調思維的全面性與深刻性。這是兩種不同層次的訓練。經歷這兩種訓練之后，知識或技能才能真正形成“產生式”。

參考文獻：

[1] 張景中.感受小學數學思想的力量——寫給小學數學教師們[J].人民教育，2017（18）.

[2] 鮑建生，周超.數學學習的心理基礎與過程[M].上海：上海教育出版社，2009.