小學數學模型思想培養探微

華兵

摘要：數學模型思想比較抽象，對仍以直觀形象化思維為主的小學生來說有一定的難度，但可以在日常教學中開展滲透式培養，為學生關鍵能力和必備品格的形成奠定基礎。《因數與倍數》一課教學，從現實生活或具體情境中抽象出數學模型，并用符號、字母等表示出模型，再運用模型解決實際問題。

關鍵詞：小學數學模型思想《因數與倍數》

數學模型，即“把某種事物系統的主要特征、主要關系抽象出來，用數學語言概括地或近似地表述出來的一種數學結構”。小學數學中的數學模型主要有數的概念、計算法則、公式、性質、數量關系等。數學模型思想就是通過對這些數學模型的研究來解決數學問題的一種數學思想方法。數學模型思想比較抽象，對仍以直觀形象化思維為主的小學生來說有一定的難度，但可以在日常教學中開展滲透式培養，為學生關鍵能力和必備品格的形成奠定基礎。具體地，可從現實生活或具體情境中抽象出數學模型，并用符號、字母等表示出模型，再運用模型解決實際問題。下面以《因數與倍數》一課教學片段為例加以說明。

一、在具體實例中抽象提取模型

【片段1】

師你能用12個相同的小正方形擺成幾種不同形狀的長方形？分別說一說你是怎么擺的，并用乘法算式表示出來。

（學生交流擺法和算式：1×12=12、2×6=12、3×4=12。）

師以3×4=12這個算式為例，在數學上我們說3是12的因數，12是3的倍數。能單獨說3是因數，12是倍數嗎？

生不能。因數與倍數是指兩個數之間的關系，所以一定要說清楚哪個數是哪個數的因數，哪個數是哪個數的倍數。

師你能再把另外兩個乘法算式像這樣說給你的同桌聽嗎？

（學生交流。）

師觀察剛剛用小正方形拼長方形時得到的三個算式，有什么共同的特點？

生都是乘法算式。

生都是自然數的算式。

生積都是12。

師那說明這些都是12的因數。12還有其他因數嗎？5是不是12的因數？

生不是，因為5×2.4=12，2.4不是自然數。

師所以在研究因數與倍數時，所指的數一般都是非0的自然數。（稍停）請同學們自己想一個算式，并說一說誰是誰的因數，誰是誰的倍數。

（學生交流。）

師你們在舉例時都依據了什么？

生（同步上臺板演并說明）我們想到的是（）×（）=（）。第一個乘數和第二個乘數就是乘積的因數;乘積就是第一個乘數的倍數，也是第二個乘數的倍數。

小學階段因數與倍數概念的教學不能完全從數學抽象的意義上展開，而要通過若干例子，指出兩個非0自然數之間存在因數與倍數的關系，從而體會因數與倍數概念。所以這里讓學生充分舉例，總結發現兩個非0自然數之間的關系，從而在具體實例中抽象、提煉出因數與倍數的數學模型——（）×（）=（）。

二、在圖示和辨析中解讀、理解模型

【片段2】

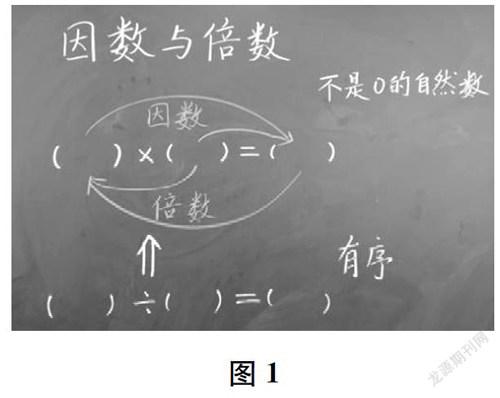
師剛才他們的發言大家都明白了嗎？（同步板書，見圖1）我們再畫一些箭頭，就更容易理解了。

圖1

（教師出示如下判斷題。學生判斷后交流。）

1.?因為3×1=3，所以3是3的倍數，3也是3的因數。（）

2.?因為3×5=15，所以3是因數，15是倍數。（）

3.?因為8÷2=4，所以2是8的因數，8是2的倍數。（）

4.?因為10×3.2=32，所以10是32的因數。（）

師第3題你是怎么想的？

生因為除法是乘法的逆運算，所以可以將除法轉化為乘法。8÷2=4可以轉化為4×2=8，那么就可以得到2是8的因數，8是2的倍數，所以這題是對的。

師也就是說，因數與倍數的背后總能找到相應的乘法算式或者除法算式。

模型剛抽象、提取出來，一部分學生還沒有充分理解，這就需要教師在這一難點處放慢腳步，帶領學生解讀、理解模型。這里，首先通過板書，讓學生重點看圖中箭頭，理解因數與倍數之間的關系;然后通過判斷題，加深學生對模型正向和反向的理解。

三、在問題解決中應用深化模型

【片段3】

師那任意給你一個數，你能找到它的所有因數嗎？比如36，先獨自想一想，然后全班交流。

生只要兩個數乘積等于36，那么這兩個數就都是36的因數。

生我有補充。只要想（）×（）=36，填進算式的兩個數就是36的因數。

生用除法也可以，可以想36÷（）=（），括號里的兩個數就是36的因數。

師同學們真棒！用我們之前的乘法算式“模板”，就簡便地找到了36的因數。那36最小的因數是多少？最大的呢？

生因為（非0的）自然數最小是1，且符合算式，所以最小的因數是1，那么，最大的因數就是36。

師我們繼續來研究一個數的倍數。以3為例，你能找出3的所有倍數嗎？

生只要找3乘幾，用3和（非0的）自然數相乘，積就是3的倍數。

生只要從3開始，后面依次加3，得到的數就是3的倍數。

生我想到的是3×（）=（），從1開始乘自然數，乘出的結果就是3的倍數。

師這三位同學想的方法都很好！其中第三位同學又想到了一個乘法算式。看來，乘法算式在找一個數的倍數時，也是至關重要的。

師3的倍數還有什么特點？

生根據算式3×（）=（），因為自然數有無窮多個，所以3的倍數也有無窮多個。

師那有最大的3的倍數嗎？

生沒有。

師最小的呢？

生（非0的）自然數中1最小，根據算式，3的最小的倍數是3×1=3。

師也就是3本身。看來，同學們學得都很好，那讓我們來做個小游戲吧！老師這里有個神秘的數，并且和這里的六張牌上的數字有關，這些數字都是從小到大排列的，你能根據這些牌找出這個神秘的數嗎？

生（自信地）能！

師那我們來試試看吧。如果這些牌上的數字都是這個數的因數。你認為你只要翻開哪些牌，就能找出這個數？

生只要翻開最后一張，因為一個數最大的因數是它本身。

師如果不允許翻開最后一張呢？

生翻開第二張和第五張，或者第三張和第四張，因為它們的乘積就是這個數。

師如果這些牌都是這個數的倍數，只要翻開哪些牌，就能知道這個數？

生只要翻開第一張，因為一個數最小的倍數就是它本身。

生翻開第二張也行，因為第二張是這個數的2倍，只要除以2就知道了。

生翻開任意一張都可以，只要拿這一張除以它的位置（序數），都能得到這個數。

在學生建構、理解模型之后，通過猜卡片數字的游戲，引導學生應用模型。特別是找一個數的倍數，學生不僅想到第一個數就是要找的數，而且知道原因（最小的倍數就是數本身），還知道翻開任何一張牌都能找出這個神秘的數。這正是“（）÷（）=（）”模型已深深扎根在學生心中、融入學生知識結構中的最好表現。

參考文獻：

[1]?顧泠沅.數學思想方法[M].北京：中央廣播電視大學出版社，2004.