淺析立幾中點(diǎn)線、點(diǎn)面的距離問題

顧晶晶

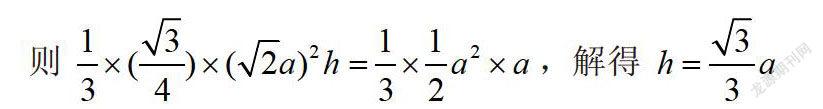
摘 要：立體幾何向來是高中數(shù)學(xué)中的一個(gè)重難點(diǎn)問題，也是備受關(guān)注的研究熱點(diǎn)。本文主要論述的是立幾當(dāng)中點(diǎn)線或點(diǎn)面距離的幾種求解思路及學(xué)習(xí)方法，以促進(jìn)學(xué)生對(duì)此類問題邏輯思維能力和解題能力的提升。

關(guān)鍵詞：立體幾何;點(diǎn)線;點(diǎn)面;線線（線面）垂直

立體幾何涵蓋了作圖能力、空間想象能力、邏輯思維能力和基本運(yùn)算能力等。其中點(diǎn)到直線（或平面）距離問題常令學(xué)生頭疼不已，作為工作十多年的數(shù)學(xué)老師也是看在眼里，急在心里。于是筆者對(duì)這類問題作了如下總結(jié)和研究，以期在今后的教學(xué)實(shí)踐中起到更好的效果。

一、直接思路

（一）定義法

此法應(yīng)用的前提是學(xué)生能夠掌握住點(diǎn)線（點(diǎn)面）距離基本定義、會(huì)看圖、能夠運(yùn)用基本定理等尋求或是證明線線垂直、線面垂直。

例1在正方體ABCD-A1B1C1D1中，求：（1）A1到AC1的距離

（2）C1到面ABB1A1的距離

分析：（1）中的問題是點(diǎn)到直線的距離，很明顯我們希望涉及的三個(gè)點(diǎn)出現(xiàn)在同一個(gè)平面內(nèi)，故連接A1C1，A1B，而A1BC1是以面對(duì)角線為邊的正三角形，故轉(zhuǎn)化為求此三角形BC1邊上高的問題（線線垂直問題）。∴dA1-BC1=a

（2）∵C1B1⊥面ABB1A1，

∴C1B1長為點(diǎn)C1到面ABB1A1的距離，長度為a

注明：有時(shí)題目本身沒有提供圖形，則要自己認(rèn)真、工整地畫出立體圖形，并區(qū)分好虛實(shí)線，再結(jié)合直觀圖來理解，才能順利解題。

（二）性質(zhì)法

例2正三棱錐P-ABC，已知側(cè)棱長為2cm底面周長為3cm，求此棱錐的高。

分析：由性質(zhì)知道頂點(diǎn)與底面中心的連線就是它的高，接下來的問題就是作輔助線解題。設(shè)底面中心為O，連接PO，則PO為正三棱錐P-ABC的高。再連接AO并延長交BC于E點(diǎn)，根據(jù)對(duì)稱性關(guān)系可以知道AE⊥BC，∵底面周長為3cm∴BC=1，AE=，再據(jù)比例關(guān)系可得AO=AE=，而PO⊥底面ABC。∴在Rt△POA中：易得PO=，即為所求的高。

（三）定理法

例3：已知ABCD為矩形，AB=3，BC=4，且PA⊥面ABCD，PA=1。

求：（1）C點(diǎn)到面PAB的距離

（2）P點(diǎn)到直線BD的距離

分析：（1）∵PA⊥面ABCD，∴PA⊥BC①

∵AB為PB在面ABCD中的射影，而在矩形中AB⊥BC

由三垂線定理得PB⊥BC②。故由①②得BC⊥面PAB

∴BC長即為所求C點(diǎn)到面PAB的距離，即為4。

（2）如果采用像例1（1）中連接PB，PD來構(gòu)造一個(gè)平面是行不通的，因?yàn)镻B≠PD。則只能添加另外的輔助線，過P作PE⊥BD，相對(duì)于面ABCD而言PE為其一條斜線，聯(lián)想三垂線定理。故連線段AE，∵PA⊥面ABCD，∴AE為射影，∵PE⊥BD，∴AE⊥BD，則在Rt△BAD中，由面積相等法得：AE=12/5。∵PA⊥面ABCD，∴PA⊥AE。在Rt△PAE中，PE2=PA2+AE2，PE=13/5，即為所求P點(diǎn)到直線BD的距離。

間接思路（體積相等法）

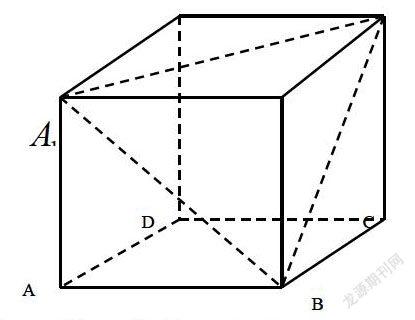
例4、棱長為a的正方體ABCD-A1B1C1D1中，求B1點(diǎn)到面A1BC1的距離.

分析：顯然B1A1，B1C1，B1B與面A1BC1皆非垂直關(guān)系，故定義法行不通，易判斷B1-A1BC1為正三棱錐，而A1B1⊥面B1BC1，即將A1視為頂點(diǎn)，那么B1BC1就是它的底面，故可以從兩個(gè)角度來表示出三棱錐B1-A1BC1的體積，設(shè)B1點(diǎn)到面A1BC1的距離為h，三角形A1BC1的邊長為，三角形B1BC1的直角邊長為a，面B1BC1上的高為a，代入體積關(guān)系式：

則，解得

用體積相等法來解題，其實(shí)與平面幾何中的面積相等法有著異曲同工之妙。

點(diǎn)到直線（或平面）距離問題是高中數(shù)學(xué)的重要內(nèi)容之一，雖然題型多變，但萬變不離其宗。以上是我對(duì)這類知識(shí)點(diǎn)的一些理解和感悟，希望同學(xué)們?cè)诮窈筮@類問題學(xué)習(xí)中多思考、多歸納、多總結(jié)，從而帶來事半功倍的效果。

參考文獻(xiàn)

[1]徐明杰.淺談空間想象能力的培養(yǎng)[J].數(shù)學(xué)通報(bào).2005，（6）

[2]侯慶盛.談?wù)匋c(diǎn)面距離的求解策略[J].數(shù)學(xué)教學(xué)研究.2002，（4）