巧用摩擦角，妙解高考題

范良蘭

摘 要：摩擦角在高中的教學中并沒有要求，但是在解高考題中的應用，相對于常規解法，利用摩擦角可以有事半功倍的的效果，也更能體現本學科的學科素養。

關鍵詞：摩擦角;解題

一、試題出處：2012年高考全國新課標理綜卷24題

原題：拖把是由拖桿和拖把頭構成的擦地工具（如圖）。設拖把頭的質量為m，拖桿質量可以忽略;拖把頭與地板之間的動摩擦因數為常數μ，重力加速度為g，某同學用該拖把在水平地板上拖地時，沿拖桿方向推拖把，拖桿與豎直方向的夾角為θ。

（1）若拖把頭在地板上勻速移動，求推拖把的力的大小。

（2）設能使該拖把在地板上從靜止剛好開始運動的水平推力與此時地板對拖把的正壓力的比值為λ。已知存在一臨界角θ0，若θ≤θ0，則不管沿拖桿方向的推力多大，都不可能使拖把從靜止開始運動。求這一臨界角的正切tanθ0。

二、講解過程

1、審題

就是教學生的審題方法。審題實質上還是理解能力，理解題目所涉及的物理現象和物理過程，明確題目中所提供的條件和要求。

（1）、抓住關鍵字眼，突出物理狀態。

（2）、分析已知條件、挖掘題目隱含條件。

拖把是由拖桿和拖把頭構成的擦地工具（如圖）。設拖把頭的質量為m，拖桿質量可以忽略;拖把頭與地板之間的動摩擦因數為常數μ，重力加速度為g，某同學用該拖把在水平地板上拖地時，沿拖桿方向推拖把，拖桿與豎直方向的夾角為θ。

（1）若拖把頭在地板上勻速移動，求推拖把的力的大小。

（2）設能使該拖把在地板上從靜止剛好開始運動的水平推力與此時地板對拖把的正壓力的比值為λ。已知存在一臨界角θ0，若θ≤θ0，則不管沿拖桿方向的推力多大，都不可能使拖把從靜止開始運動。求這一臨界角的正切tanθ0。

2、解題

（1）拖把頭在地板上勻速移動，求推拖把的力的大小

對拖把受力分析，畫出受力示意圖：由于勻速移動，由共點力平衡條件可得：

水平方向：Fsinθ=ff=μN豎直方向：N=mg+Fcosθ

解得：F=方法1：把在地板上從靜止剛好開始運動的水平推力即F水平=fm

依題意有：λ==

不管沿拖桿方向的推力多大，都不可能使拖把從靜止開始運動則應滿足：Fsinθ≤fm

fm=λNN=mg+Fcosθ

三式聯立得：Fsinθ≤λ（mg+Fcosθ）

即（sinθ-λcosθ）≤λmg/F

不管沿拖桿方向的推力多大，此式恒成立，即F趨于無窮大時，（sinθ-λcosθ）≤0

解得：tanθ≤λ故tanθ0=λ

方法2：用摩擦角來解決這一問題

令地板對拖把的正壓力N與最大靜摩擦f的合力為R，物理學中將此合力稱為全反力，此合力與正壓力N之間的夾角α稱為摩擦角，由圖可得：tanα==λ即α角的大小由λ決定。當外力F與正壓力之間夾角為θ時，則使物體運動的動力

Fx=Fytanθfm=Ntanα=（mg+Fy）tanα

比較兩式可得：若θ≤α時，無論外力F多大都有Fx≤fm，（即滿足題中不管沿拖桿方向的推力多大，都不可能使拖把從靜止開始運動（這就是生活中遇到的自鎖現象）。故臨界角的正切tanθ0=λ

三、試題拓展及試題的意義

1.試題拓展：

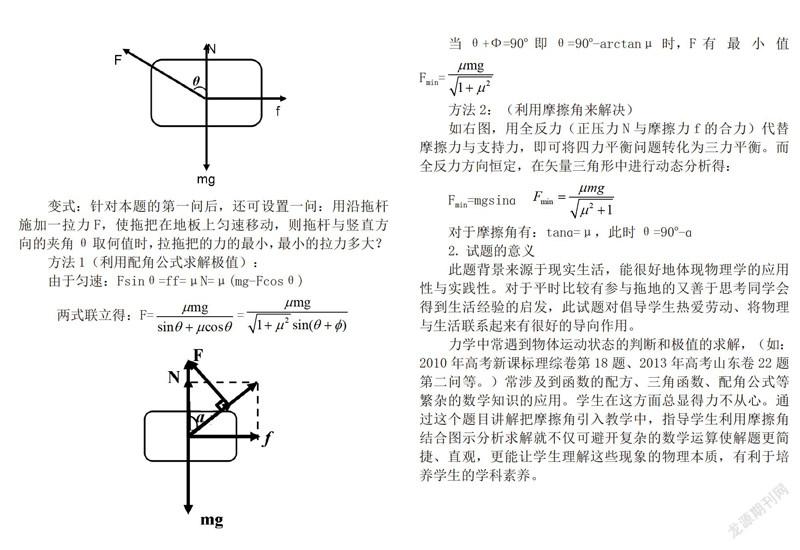
變式：針對本題的第一問后，還可設置一問：用沿拖桿施加一拉力F，使拖把在地板上勻速移動，則拖桿與豎直方向的夾角θ取何值時，拉拖把的力的最小，最小的拉力多大？

方法1（利用配角公式求解極值）：

由于勻速：Fsinθ=ff=μN=μ（mg-Fcosθ）

兩式聯立得：F==

當θ+Ф=90o即θ=90o-arctanμ時，F有最小值Fmin=

方法2：（利用摩擦角來解決）

如右圖，用全反力（正壓力N與摩擦力f的合力）代替摩擦力與支持力，即可將四力平衡問題轉化為三力平衡。而全反力方向恒定，在矢量三角形中進行動態分析得：

Fmin=mgsinɑ

對于摩擦角有：tanɑ=μ，此時θ=90o-ɑ

2.試題的意義

此題背景來源于現實生活，能很好地體現物理學的應用性與實踐性。對于平時比較有參與拖地的又善于思考同學會得到生活經驗的啟發，此試題對倡導學生熱愛勞動、將物理與生活聯系起來有很好的導向作用。

力學中常遇到物體運動狀態的判斷和極值的求解，（如：2010年高考新課標理綜卷第18題、2013年高考山東卷22題第二問等。）常涉及到函數的配方、三角函數、配角公式等繁雜的數學知識的應用。學生在這方面總顯得力不從心。通過這個題目講解把摩擦角引入教學中，指導學生利用摩擦角結合圖示分析求解就不僅可避開復雜的數學運算使解題更簡捷、直觀，更能讓學生理解這些現象的物理本質，有利于培養學生的學科素養。