六參數粘彈性阻尼耗能減震系統非平穩地震響應分析的精細積分法

李創第 昌明靜 柏大煉 王博文

摘? ? 要：針對六參數粘彈性耗能減震系統，結合虛擬激勵法，給出了非平穩地震響應分析的精細分析法.對于設置的支撐六參數粘彈性阻尼耗能系統的運動方程，首先，采用高效的虛擬激勵法，將非平穩隨機地震激勵化為確定性荷載;然后，利用擴階法，得到系統的狀態方程;最后，給出了響應的精細積分解析解.并通過算例驗證本文方法的精確性與實用性，為該方法推廣應用于復雜大型結構的耗能減震工程提供新途徑.

關鍵詞：六參數粘彈性;精細積分法;虛擬激勵法;耗能減震系統;非平穩地震響應

中圖分類號：TU311.3? ? ? ? ? DOI：10.16375/j.cnki.cn45-1395/t.2019.04.003

0? ? 引言

粘彈性阻尼裝置控制結構振動是一種有效且廣泛使用的被動控制方法，其模型主要有Maxwell模型、Kelvin模型、六參數模型等[1-3].其中，六參數模型計算參數便于實驗數據擬合，具有通用性和工程實用性的特點，是一種實用的粘彈性阻尼器減震模型[4-6].為此，對該模型的耗能減震系統響應進行深入分析，具有重要的理論價值和實際意義.

在工程中，應用較多的是Priestley[7]提出的受演變隨機激勵非平穩隨機響應分析.針對此響應分析，傳統分析方法有CQC計算格式[8]和SRSS近似格式[9].但因這兩種方法計算公式復雜，計算過程繁瑣且成本巨大，計算效率難以在工程上廣泛應用.林家浩等[10]提出的虛擬激勵法，將隨機激勵化為確定性荷載，簡化計算過程，節省了計算時間且結果依然相同，改善了傳統方法的限制.虛擬激勵法的提出解決了很多工程中重要而困難的問題，如大跨橋梁結構、風工程、車輛工程以及國防工程等領域，在國際上有較高的影響力[11].

在計算時程積分時，一般用Newmark，Wilson-θ等方法求解，但是這兩種方法都存在耗時較長，精度有限等問題.鐘萬勰[12]提出的精細積分法，在積分步長不受結構自振特性制約的情況下，總能算出計算機精度范圍內的結構響應.該方法目前已被廣泛地應用于熱傳導、結構動力響應、結構優化設計、偏微分方程的求解等眾多領域[13-14];精細積分方法與虛擬激勵法結合，已經成功解決了無阻尼結構的非平穩隨機地震響應分析[15-16]，但至今尚未應用于粘彈性阻尼耗能減震結構的非平穩響應分析和阻尼系統抗震動力可靠度分析.

對于耗能減震系統的運動方程，本文利用虛擬激勵法，將非平穩隨機地震激勵化為確定性荷載，利用擴階法得出系統狀態方程，并算出了響應的精細積分解析解.最終得出一套關于非平穩地震激勵下，六參數阻尼耗能減震系統簡明直觀的精細算法.

1? ? 阻尼器本構關系及系統運動方程

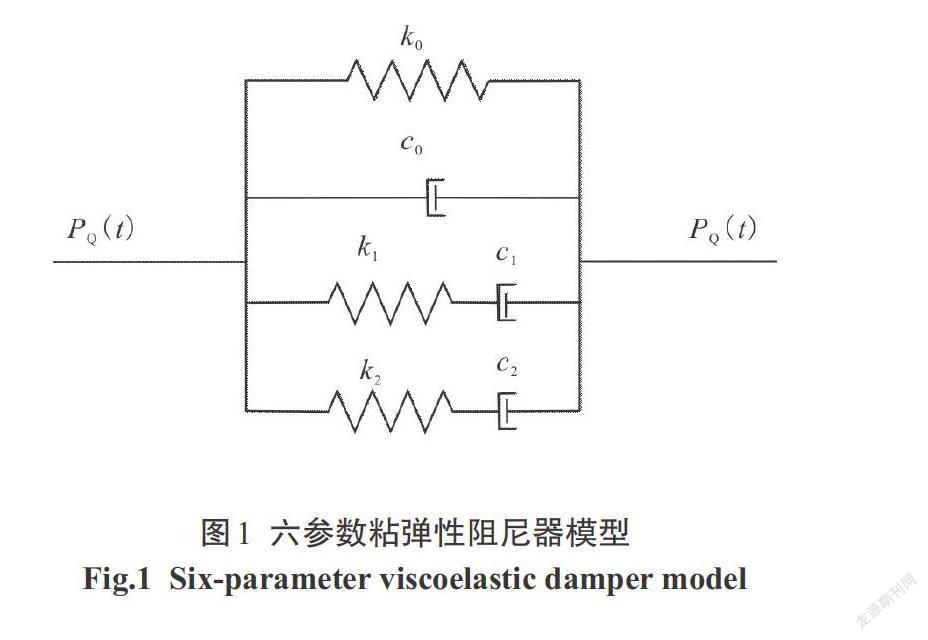
六參數粘彈性阻尼器模型如圖1所示，該粘彈性阻尼器本構關系表達式為[4]：

[PQ（t）=k0xQ+c0xQ+P1（t） +P2（t） ]? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?（1）

[P1+μ1P1=k1xQ]? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?（2）

[P2+μ2P2=k2xQ]? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? （3）

式中，[k0]為阻尼器的平衡剛度;[Pi（i=1，2）]表示六參數粘彈性阻尼器中兩支Maxwell阻尼單元的單元阻尼力;[μi=ki/ci（i=1， 2）]，[xQ]為阻尼器位移.

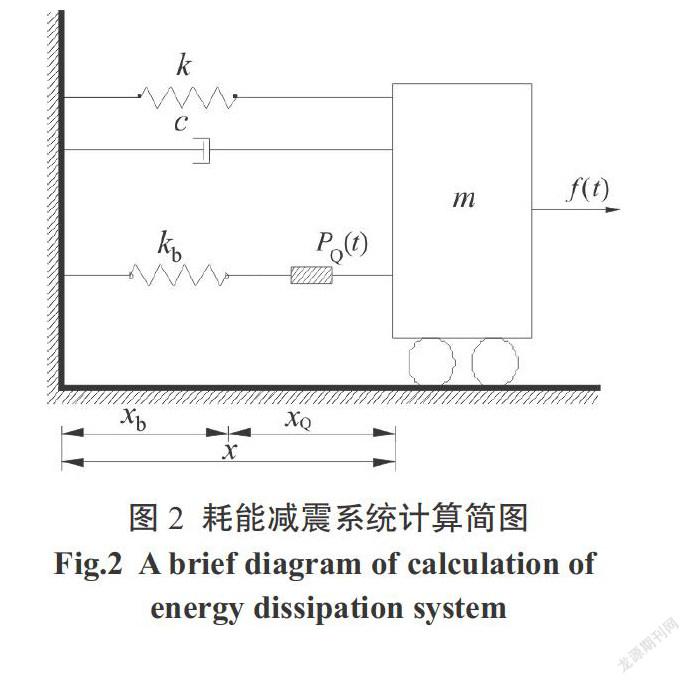
工程實際中，一般把支撐和阻尼器串聯，計算簡圖如圖2所示.[PQ]、[Pb]和[P]分別表示阻尼器受力、支撐受力和阻尼系統受力，[xb]和[x]分別為支撐和結構的位移，關系式為：

[P=PQ=Pb=kxb]? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?（4）

[xb+xQ=x]? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? （5）

結構在地震作用[f（t）]下的及運動方程為：

[mx+cx+kx+P=f（t）]? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?   ? ? ? ? ? ? （6）

2? ? 六參數粘彈性阻尼減震系統響應分析

2.1? ?非平穩地震響應的虛擬激勵法

實際地震中，地震發生的隨機振動過程，一般視為非平穩隨機過程，非平穩隨機過程不是各態歷經的，其各種統計信息隨時間變化而變化.地震動過程通常包含兩個非平穩過程，一種是強度非平穩，另一種是頻率非平穩，為考慮這兩種情況的共同影響，通常采用Priestley[7]建議的演變功率譜：

[xg（t）=-∞+∞a（ω，t）eiωtdα（ω）=a（ω，t）xf（t）]? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?（7）

其中，[a（ω，t）]是滿足[a（ω，t）=a*（-ω，t）]的確定性非均勻調制函數，*表示共軛，[xg]地震動地面加速度，[xf（t）]為零均值平穩隨機過程，[i=-1].[α（ω）]滿足下列過程：

[xf（t）=+∞-∞eiωtdα（ω）]? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?（8）

[Edα*（ω1）dα（ω2）=δ（ω1-ω2）Sxf（ω1）dω1dω2]? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?（9）

[Sxf]（ω）為[xf]的功率譜密度函數.常用的有Kanai-Tajimi激勵譜、Clough-Penizien譜、胡聿賢譜[10]等.

根據林家浩的虛擬激勵法理論，如果構造非平穩虛擬地震激勵為：

[xg（ω， t）=Sxf（ω）a（ω，t）eiωt]? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? （10）

設在[xf（ω， t）]產生的響應表示為[v（ω， t）]，那么響應的自譜密度即可表示為：

[Svv（ω， t）=v*（ω， t）v（ω， t）=I*（ω， t）I（ω， t）Sxf（ω）]? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? （11）

式中，[I（ω， t）=0th（t-τ）a（ω， τ）eiωτdτ].

把非平穩虛擬地震激勵（10） 代入振動方程（6）中得：

[mx+cx+kx+P=-mSxf（ω）a（ω， t）eiωt]? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?（12）

2.2? ? 六參數粘彈性阻尼減震的精細積分法

對于上面建立的非平穩虛擬激勵的動力學模型，引入響應變量：

[v（t）=xxxQP1P2T]? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? （13）

由式（12）結合恒等式[x=x]和式（1）—式（5），寫入狀態方程為：

[Bv（t）+Av（t）=F]? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? （14）

其中，

[B=cmc000m000000c00000-c11000-c201] [，? A=k0k0110-m000-kb0k0+kb11000μ100000μ2]，

[F=-mSxf（ω）a（ω， t）eiωt， 0， 0， 0， 0T]

式（14）可改寫為：

[v=Hv+r]? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? （15）

式中，

[H=-B-1A ， r=B-1F]? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?（16）

當步長足夠小，即[t∈（tk， tk+1）]，假定激勵荷載變化是線性的，有：

[r=r0+r1（t-t0）]? ? ?   ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? （17）

式中，[r0]與[r1]是時不變向量，則方程（15）的解為：

[v（tk+1）=T（τ）[v（tk）+H-1（r0+H-1r1）]-H-1（r0+H-1r1+r1τ）]? ? ? ? ? ? ? ? ? ? ? ? （18）

式中，[τ=tk+1-tk]為積分步長.上式中出現的矩陣[T（τ）]的計算，首先將積分步長[τ]內部細分為[m=2N]等分，即：

[Δt=τ/m=2-Nτ]? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? （19）

一般取[N=20]，于是[Δt≈10-6τ]，[Δt]一般遠小于結構的自振周期.

[T（τ）=（eHΔt）m≈（I+HΔt+（HΔt）2/2！+（HΔt）3/3！+（HΔt）4/4！）m=（I+Ta0）m]? ? ? ? ? ? （20）

令：

[I+Tai=（I+Ta，i-1）2=（I+2Ta，i-1+Ta，i-1Ta，i-1） ;i=1，2，…，N]? ? ? ? ? ? ? ? ? ? ? ?（21）

得：

[Tai=2Ta，i-1+Ta，i-1Ta，i-1]? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?（22）

那么，

[I+TaN=（I+Ta，N-1）2=（I+Ta，N-2）4=…=（I+Ta0）m=T（τ）]? ? ? ? ? ? ? ? ? ? ? ? ? ? （23）

計算得到[Ta1 ， Ta2 ， …， TaN]，進而得到[Τ（τ）]，即可由式（18）得到各響應的解析解.

以上[T（τ）]的推導過程均為精確推導，可以看出只有一處近似，即式（20）的計算過程中忽略了[Δt5]及更高階的項，其數量級已經超過[10-30O（τ5）]，遠超過使用計算機的精度范圍.該方法過程簡明易于理解且計算較精確.

綜上步驟，六參數粘彈性耗能減震系統的位移[x（ω， t）]、速度[x（ω， t）]和阻尼器位移[xQ（ω， t）]即：

[x（ω， t）=v（1）]? ? ?   ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? （24）

[x（ω， t）=v（2）]? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? （25）

[xQ（ω， t）=v（3）]? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?; ? ? ? ? ? ? ? ? ?（26）

支撐位移[xb（ω， t）]：

[xb（ω， t）=x（ω， t）-xQ（ω， t）]? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?（27）

[P（ω， t）=kbxb（ω， t）]? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? （28）

阻尼力[P（ω， t）]可由式（28）得到，也可根據式（1）得到.

[P（ω， t）=kbxb（ω， t）]? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?（29）

阻尼力速度[P（ω， t）]可根據對應的阻尼力求導，也可由式（29）得到.

阻尼器速度和支撐速度可根據對應的位移求導得到.響應的方差由式（18）得：

[σ2v（t）=-∞+∞Svv（ω）dω]? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?（30）

3? ? 算例

某單自由度帶支撐的六參數粘彈性阻尼耗能減震系統，結構質量[m=38 600 kg]，結構剛度? ? ? ? ? ? ? [k=146.01×105 N/m]，阻尼比[s0]=0.04;阻尼器的平衡剛度[k0=0.36×105 N/m]，阻尼參數[c0=0.37×105 N?s/m]，兩個Maxwell分支單元的剛度[k1=42.08×105 N/m]，[k2=6.87×105 N/m]，阻尼? ? [c1=0.83×105 N?s/m]、[c2=2.15×105 N?s/m];支撐剛度[kb=rbk];平穩地震動[xf（t）]譜密度函數采用

[Sxf（ω）=ω4g+4ξ2gω2gω2（ωg-ω2）2+4ξ2gω2gω2S0]

[S0]為地震譜強度.[ωg=19 rad/s]，[ξg=0.65]，[S0=0.015 54 m2/s3].

1）經典階躍型調制函數，[a（t）=1 ].

2）Spanos-Solomos型調制函數[16]：

[a（ω，t）=2 ω5π t e-0.5×0.15+ω225π2t].

取5種工況，分別為[rb=0.5，? rb=0.8，? rb=1.5，? rb=10，? rb=∞].計算中步長取[τ=0.01 s].

①響應方差對比分析

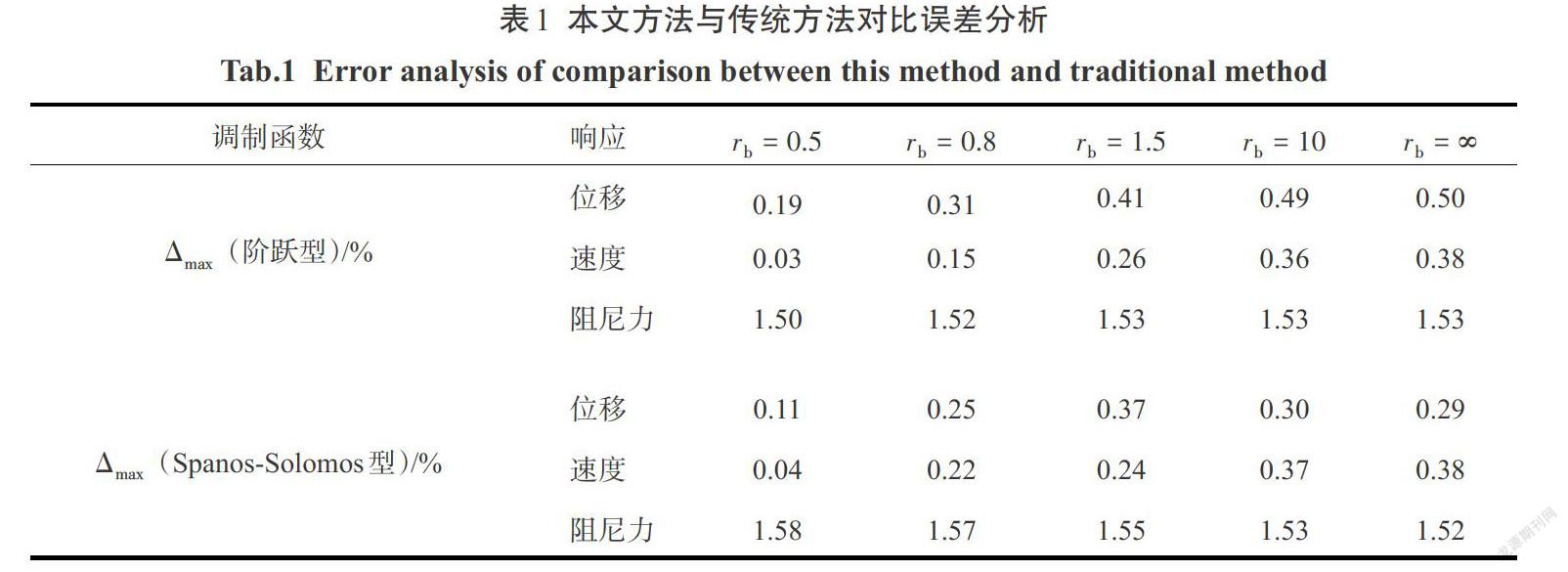
在上述兩種非平穩地震激勵下，本文方法與傳統方法求出該系統在5種工況下的位移、速度和阻尼力對比的誤差值如表1所示.

可以看出，本文方法所得響應方差誤差較小，無論[rb]取多大值，位移與速度響應方差的最大誤差[Δmax≤0.5%]，阻尼力響應方差誤差[Δmax]在[1.5%]左右，數值計算結果較為理想，從而驗證了本文方法的精確性與可行性.

②結構及各阻尼構件的響應方差計算

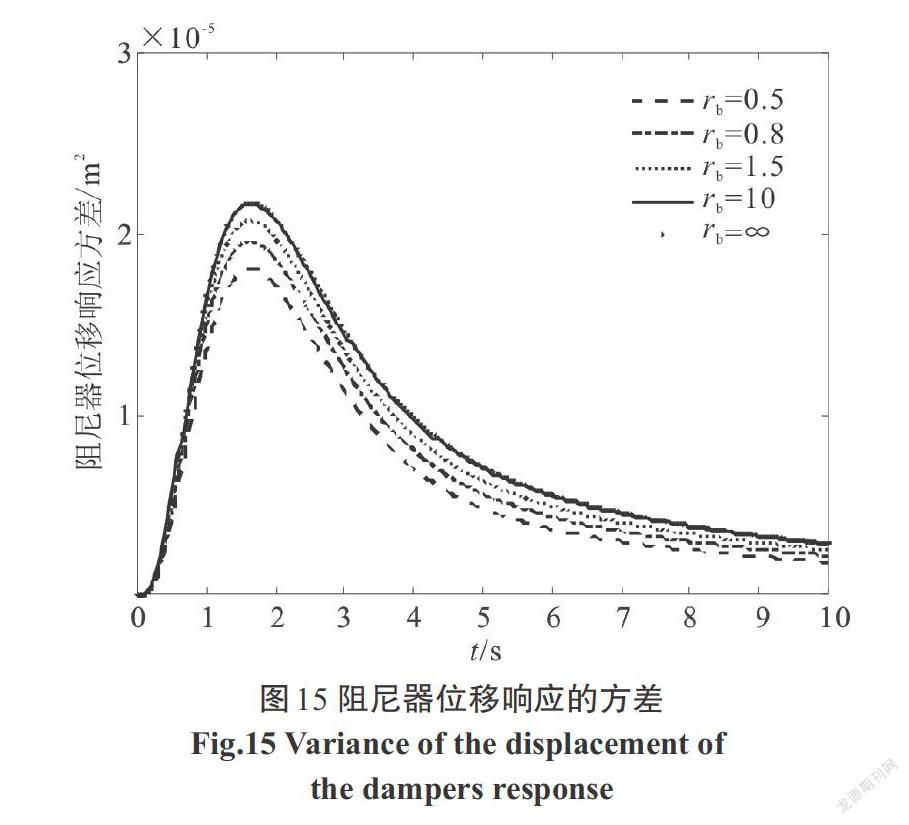
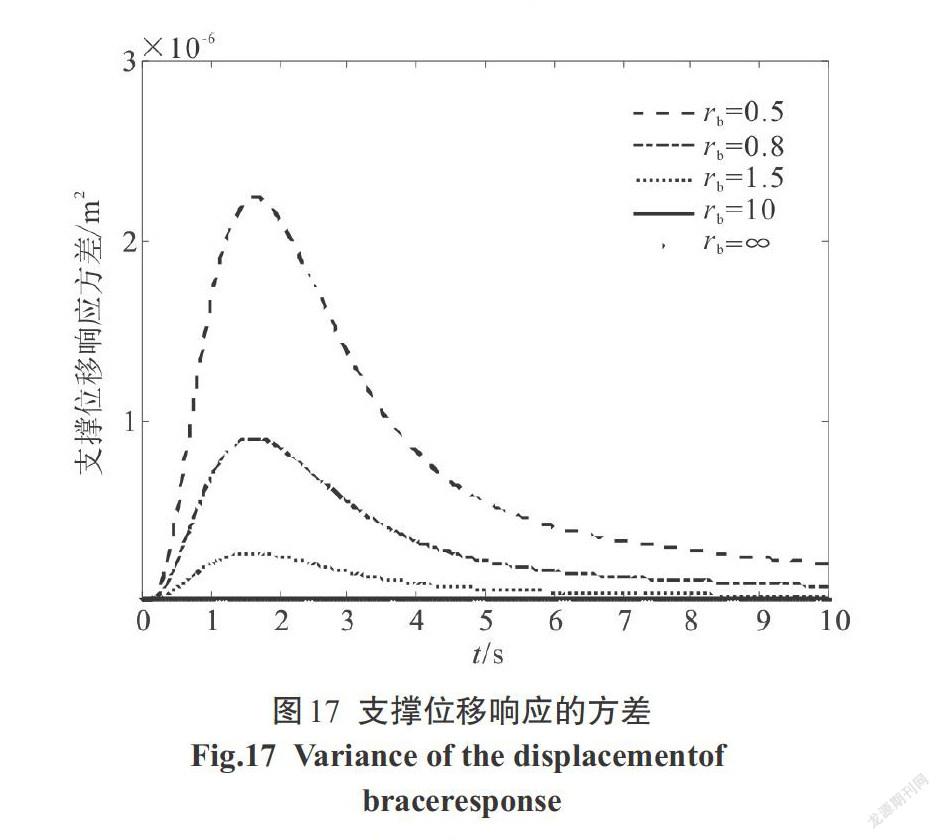
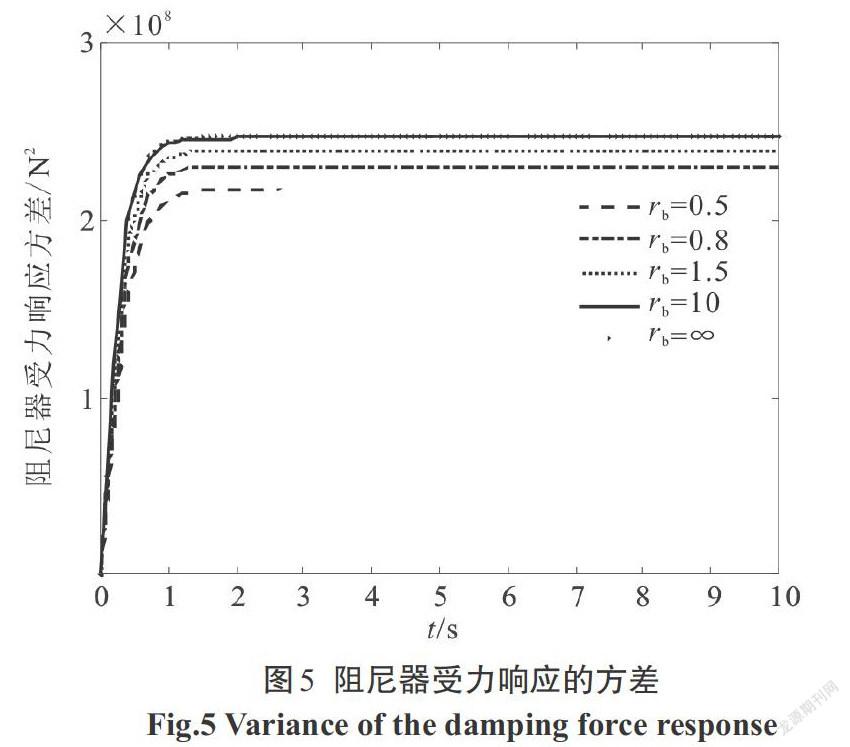
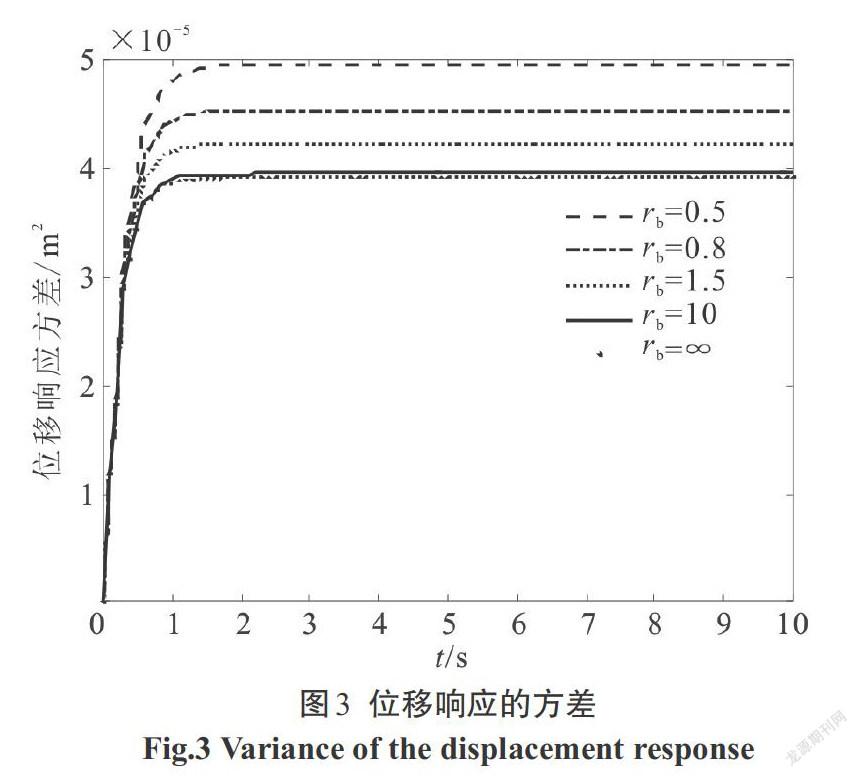
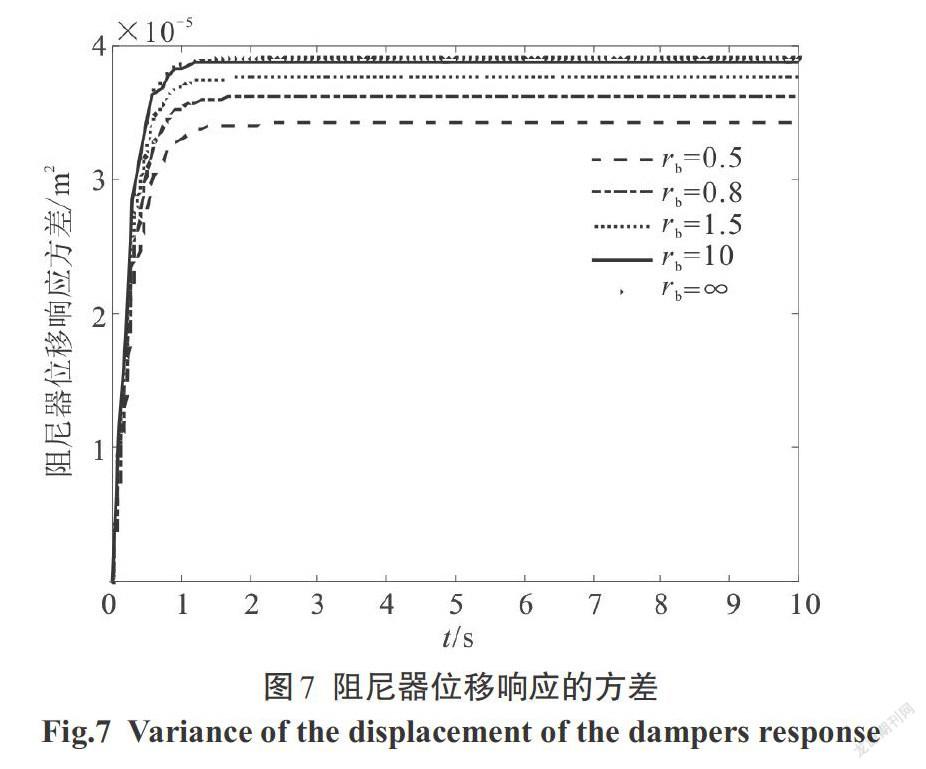
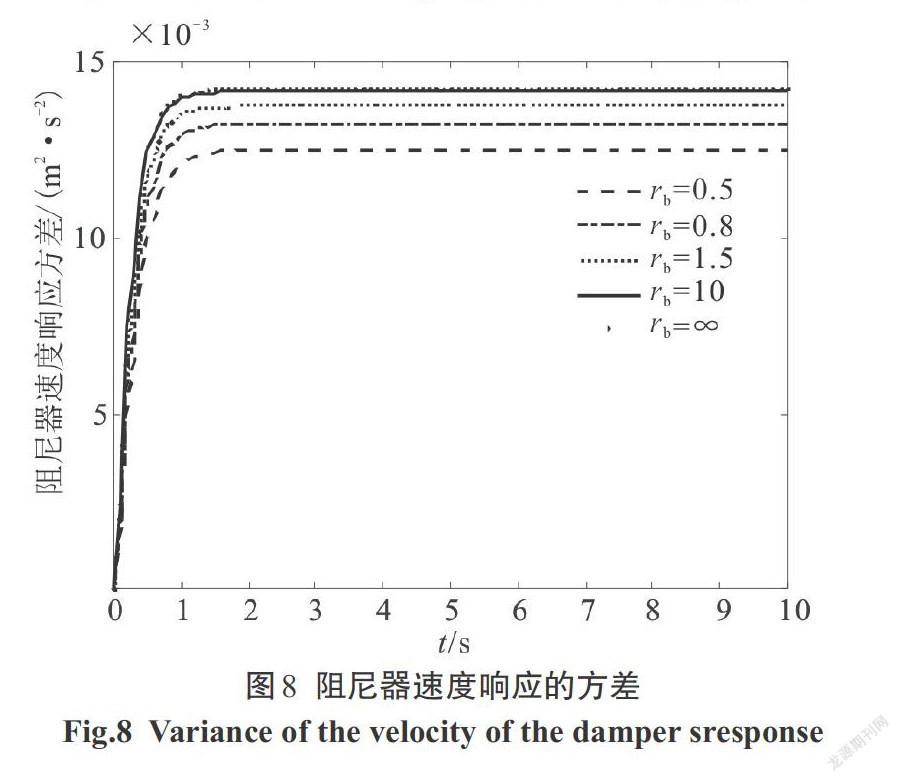
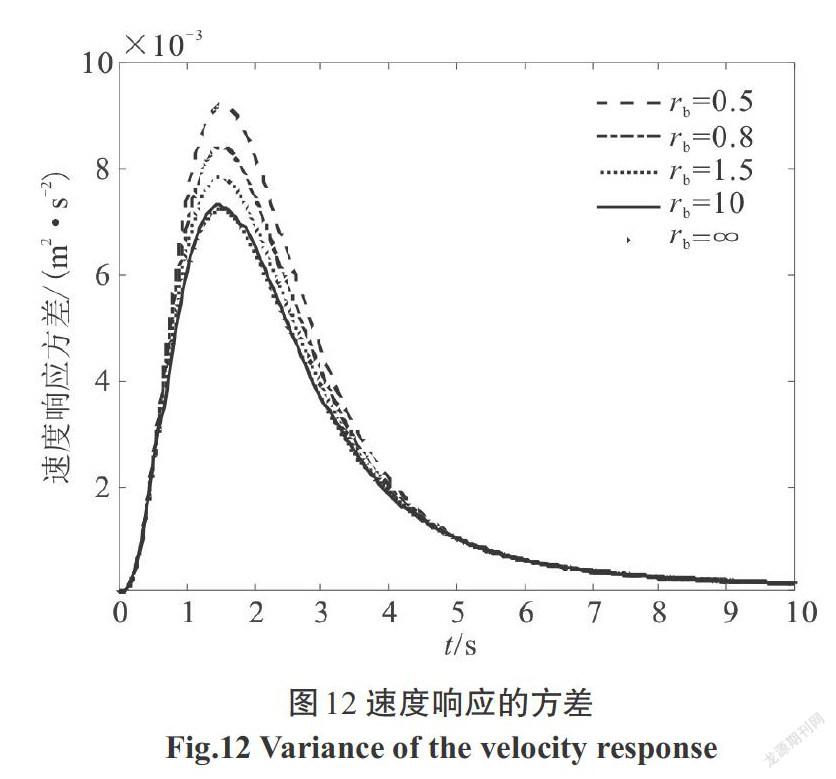
利用本文方法求出結構位移、速度，阻尼器受力、受力速度，阻尼器位移、速度，支撐位移、速度的響應方差，圖像如下，階躍型調制非平穩響應圖像如圖3—圖10，Spanos-Solomos型調制非平穩響應圖像如圖11—圖18.

以上兩種調制非平穩隨機地震激勵下，對結構及各減震構件響應方差的數值分析可以看出：

1）支撐剛度[kb]對結構減震效果影響較大.在5種[kb]的影響下，隨著支撐剛度[kb]的增加，結構的位移（對應圖3、圖11）、速度（對應圖4、圖12），支撐的位移（對應圖9、圖17）、速度（對應圖10、圖18）等響應方差均呈現減小趨勢.但是當支撐剛度[kb≥10 k]后，結構位移和速度響應的減小量不大.即支撐剛度越大，減震效果越好，但是當支撐剛度足夠大時，減震效果改善不明顯且不夠經濟.

2）支撐位移和速度響應方差，與結構位移響應方差變化趨勢保持一致，阻尼器位移和速度響應方差，與阻尼器受力響應方差變化趨勢保持一致.支撐剛度[kb]越大時，阻尼器的位移、速度及阻尼器兩端受力均越大，對應圖5—圖8和圖13—圖16可以看出.阻尼器的位移、速度和兩端受力的大小，必然將影響構件的動力可靠度及性能.

4? ? 結論

在六參數粘彈性阻尼耗能減震系統的非平穩隨機響應分析中，化隨機激勵為虛擬激勵，得出系統的響應的精細積分法響分析法，經分析得出如下結論：

1）本文方法與傳統方法對比精度較高，驗證本文方法的精確性與可行性，說明本文所獲得的非平穩響應的解析解，對于六參數粘彈性耗能減震系統具有較好的工程適用性.

2）本文方法不僅可應用于此類耗能結構響應分析，而且可應用于各減震構件基于泊松過程的抗震動力可靠度分析，為虛擬激勵-精細積分法開辟了新的應用領域.

3）支撐剛度的變化對結構和各減震構件的響應有很大影響，該研究對于系統中減震構件參數的選用具有一定的參考價值.

參考文獻

[1]? ? ?CHRISTOPOULOS C，FILIATRULT A. Principle of passive supplemental damping and seismic isolation[M]. Pavia，Italy：IUSS Press，2006.

[2]? ? ?王燁華，周云，丁鯤. 粘彈性阻尼減震結構研究與應用的新進展[J].防災減災工程學報，2006，26（1）：109-121.

[3]? ? ?CHANG K C，LIN Y Y. Seismic response of full-scale structure with added viscoelastic dampers[J].Journal of Structural Engineering， 2004，130（4）： 600-608.

[4]? ? ?MAZZA F，VULCANO A. Control of the earthquake and wind dynamic response of steel-framed buildings by using additional braces and/or viscoelastic dampers[J]. Earthquake Engineering and Structural Dynamics，2011，40（2）：155-174.

[5]? ? ?李創第，劉鵬，葛新廣，等. 六參數實用粘彈性阻尼器單自由度減震系統非平穩響應分析[J].廣西科技大學學報，2018，29（2）：110-118，125.

[6]? ? ?李創第，朱騰飛，柏大煉，等. 實用粘彈性阻尼器耗能結構非平穩地震響應的快速求解[J]. 廣西科技大學學報，2018，29（4）：94-102.

[7]? ? ?PRIESTLEYN M B. Power spectral analysis of nonstationary random process[J]. Journal of Sound and Vibration，1967，6（1）： 86-97.

[8]? ? ?ERNESTO H Z，VANMARCKE E H. Seismic random vibration analysis of multi-support structiral systems[J]. Journal of Engineering Mechanics，1994，120：1107-1128.

[9]? ? ?WILSON E L，KIUREGHIAN A D，BAYO E. A repiacement for the SRSS method in seismic analysis[J]. Earthquake Engineering and Structural Dynamics，1981（9）：187-192.

[10]? ?林家浩，張亞輝. 隨機振動的虛擬激勵法[M]. 北京：科學出版社，2004.

[11]? ?林家浩，張亞輝，趙巖. 虛擬激勵法在國內外工程界的應用回顧與展望[J].應用數學和力學，2017，38（1）：1-8.

[12]? ?鐘萬勰. 結構動力方程的精細時程積分法[J].大連理工大學學報，1994，34（2）：131-136.

[13]  ?高強，譚述君，鐘萬勰. 精細積分方法研究綜述[J]. 中國科學：技術科學，2016，46（12）： 1207-1218.

[14]? ?林家浩，沈為平，威廉斯. 受演變隨機地震激勵結構的精細逐步積分法[J].大連理工大學學報，1995，35（5）：600-605.

[15]? ?林家浩，張亞輝，孫東科. 受非均勻調制演變隨機激勵結構響應快速精確計算[J].計算力學學報，1997，14（1）：1-8.

[16]? ?LIN J H，ZHANG W S，MILLIAMS F W. Pseudo-exciation algorithm for nonstationary random seismic responses[J]. Engineering Structures，1994，16（4）：270-276.

[17]? ?SPAN P T D，SOLOMOS G P. Markov approximation to transient vibration[J]. Journal of Engineering Mechanies，1983，109（4）：1134-1150.

Precise integration method for non-stationary seismic response

analysis of six-parameter viscoelastic energy dissipation system

LI Chuangdi， CHANG Mingjing， BAI Dalian， WANG Bowen

（School of Civil Engineering and Architecture， Guangxi University of Science and Technology，

Liuzhou 545006， China）

Abstract： For a six-parameter viscoelastic energy dissipation system， a precise analysis method of