淺談數形結合思想在二次函數學習中的應用
摘 ?要:二次函數是初中數學里的重難點內容,涉及的知識點較多,相關題目靈活性較大,可延伸性強,數形結合可以將抽象的數字信息與具體的圖像模型聯系起來,將其應用到二次函數上,可以使學生對二次函數具有更“立體”的認識,理解更加深刻,能提高學生解決實際問題的能力。
關鍵詞:二次函數,二次方程,數形結合;
數形結合思想在二次函數教學中具有廣泛應用,主要體現在以下幾個方面:
1.從數到形
說到二次函數,通常都會將一元二次方程與其聯系起來講解,我們都知道,一元二次方程ax2+bx+c=0(a,b,c是常數,且a≠0)是否有實數根取決于Δ=b2-4ac是否大于0,當Δ>0時,方程有兩個不同的實數根,此時,我們可以引導學生聯想到:當b2-4ac>0時,與此對應的二次函數y=ax2+bx+c的圖像與x軸具有兩個交點;而當Δ=0時,方程ax2+bx+c=0有且僅有一個實數根 ,對應的二次函數圖像與x軸也只有一個交點即 ,且該點為拋物線的頂點;當Δ<0時,方程ax2+bx+c=0沒有實數根,相對應,函數圖像與x軸不存在交點。這即是二次函數中最簡單的從數學語言轉化為圖像語言的思維方式,但是在考試過程中,往往還需要進一步拓展,如當題目要求一元二次不等式ax2+bx+c>0(或<0)的解集時,轉換為圖像語言便是求函數y=ax2+bx+c的圖像中分別在一、二(<0時對應三、四)象限部分對于x的取值范圍。
2.從形到數
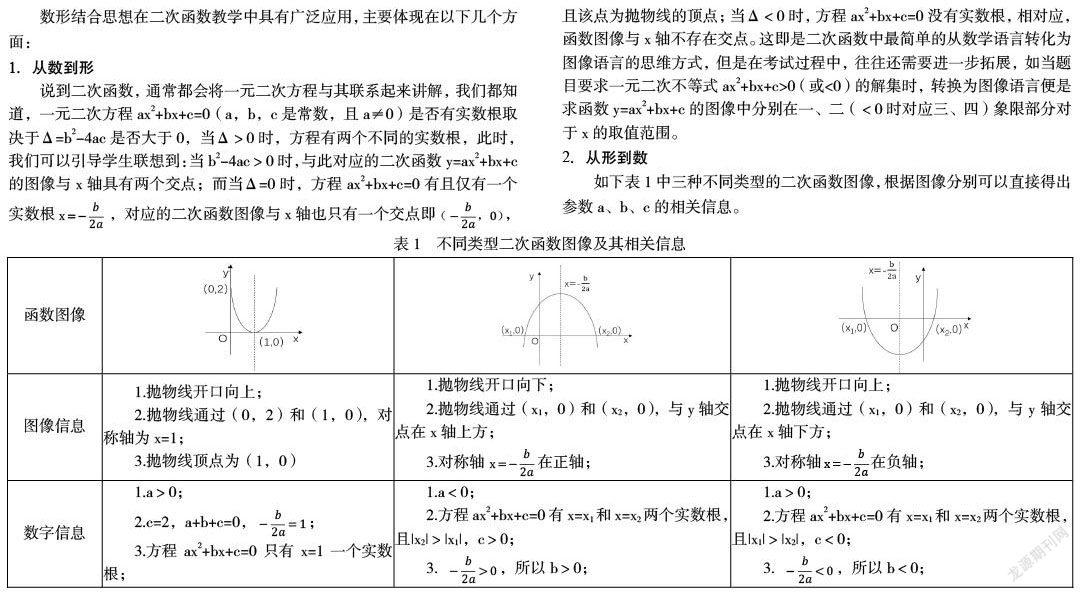
如下表1中三種不同類型的二次函數圖像,根據圖像分別可以直接得出參數a、b、c的相關信息。
參考文獻
[1] ?楊艷雯. 初中二次函數教學新思路之研究[J]. 中國校外教育,2018,641(21):82.
[2] ?張謙慧. 數形結合在二次函數中的應用[J]. 貴州教育,2002(7).
作者簡介:朱忠發(1964-),男,湖北省咸寧市人,中教一級職稱,本科學歷,主要從事中學數學教學和相關研究。

