基于HMM的高校家庭貧困生認定模型研究

謝穎 朱遠勝 馬維聰 張英

摘 要：為了將HMM的Baum-welch算法應用到高校家庭貧困生認定過程中，首先將學生的經濟狀態依據客觀情況設置為5個狀態，然后將得到的觀測數據依據外部低成本變量進行加權處理，再將加權處理后的數據按照一定的比例劃分為7個等級，對不同等級進行分段統計，并在此基礎上提出了使用HMM的Baum-Welch算法解決這個問題時構建初始化參數的方法，最后將迭代的結果依據學生貧困狀態期望百分比由高到低順序進行排序，并將結果與直接計算方法及通過實際調研得到的結論進行對比，通過對比得到了HMM算法在解決此類問題中存在的局限性，同時給出了提高預測準確性的新模型建立的建議。然后將這種方法在其它班級進行了驗證，以檢驗結論的可靠性。

關鍵詞：貧困生認定;隱馬爾可夫模型;Baum-Welch算法;期望百分比

中圖分類號：G641? ? ? ? ? ? ? 文獻標識碼：B? ? ? ? ? ? ?文章編號： 1674-2346（2019）03-0075-09

0? ? 引言

國內在定量研究高校貧困家庭學生認定方面的成果不多，田志磊[1]通過將非收入變量，如居住地與公共服務的可得性、住房條件等作為一級指標，然后構建二級指標，再構建財富指數，然后使用主成分分析法，在構建絕對家庭財富指數時采用回歸模型。胡苗苗[2]將決策理論引入經濟困難學生認定過程，將家庭經濟收入、家庭人員組成、家庭健康狀況，以及學生在校學習生活平均消費情況作為4個屬性引入到決策分析中作為評價指標，通過決策信息矩陣進行貧困生的識別。文獻[1]、文獻[2]的研究都沒有考慮特征信息的時序性。何源[3]使用了SQL Server數據挖掘技術挖掘貧困生消費行為和消費習慣，用學習的知識對新數據進行識別;周皞[4]將在校園卡上產生的各種消費數據按性質分類，通過建立消費總量和消費強度等特征向量，挖掘學生經濟狀況與消費數據的關聯規則，可以為判別高校貧困生提供輔助決策依據。文獻[3]、文獻[4]的研究都是采用微軟數據倉庫的AnalysisServices工具進行聯機數據挖掘，學習效果依賴于關聯規則的制訂。楊知玲[5]提出了從“助學貸款、家庭月收入、低保/特困戶、家庭負債、勤工助學、單親/低保”6個外部指標出發，使用決策樹模型進行高校貧困生認定，忽略了學生主體作用。

國際上，美國聯邦教育部建立了全國統一的家庭經濟困難大學生資助申請和審核系統（簡稱CPS），CPS的核心是聯邦學生資助需求計算公式：資助需求=入學成本-預期家庭貢獻，家庭預期貢獻計算復雜，要考慮家庭的年收入[1]。由于我國目前尚未建立全國范圍內的收入和誠信管理系統，因此無法實施這一方法。

本文將隱馬爾可夫模型（hidden Markov models 記為HMM）引入到高校家庭經濟困難學生認定工作中，通過研究學生在學校的日常消費行為及HMM的Baum-Welch算法估算學生經濟處于不同狀況的概率期望，通過學生校內消費的外在表現，挖掘學生經濟的內在狀況，為判斷學生的經濟狀況提供理論上的堅實依據和實際中可以操作的工具，這種算法能自動消除外圍因素，如性別差異、地區差異，以及我國在不同經濟發展時期的學生消費水平的差異等因素造成的影響，將以往通過外圍因素進行的定性或簡單定量分析轉化為通過學生主體因素為主進行的定量分析，具有普適性、易操作性，并能夠構成程序化的操作模型，從而易于在各個高校進行推廣。全文數據處理流程如圖1所示。

1? ? 數據獲取與數據劃分

1.1? ? 數據獲取

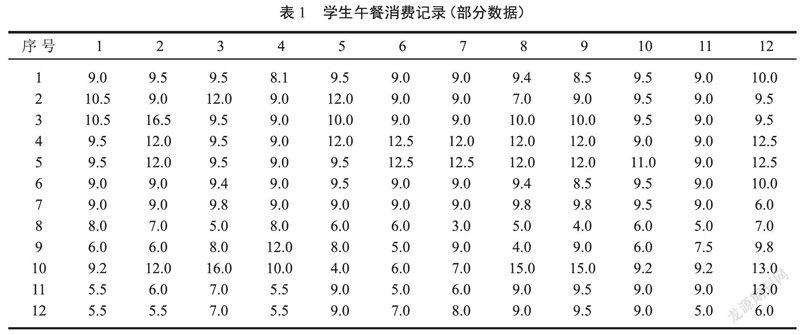
本文以€讇讇贅咝讇讇追衷簚讇讇鬃ㄒ祤讇讇裝嗉段袢≌飧靄嗉兜？7位同學從2018年3月12日至4月27日連續33次午餐記錄（周末和節假日除外），同時獲取了其它分院的另外3個班的午餐消費記錄，作為后面的算法驗證數據。個別同學的午餐數據存在缺失情況，由于采取了人工統計數據，所以缺失數據量比較少，直接以這個學生的午餐消費平均值作為缺失數據的值進行填充。所獲取的數據如表 1所示（每行代表1位同學，列是時間順序）：

1.2? ? 依據低成本變量進行數據調整

考慮學生主體消費的同時，考慮家庭因素的影響，依據文獻[1]中所述低成本變量，我們分別采集父母身體狀況、父母學歷、父母工作性質、是否單親家庭和是否孤兒作為外部因素，并分別對消費數據進行加權處理。所謂低成本變量是指容易獲得，并且很大程度上不失真的特征信息，之所以要調整數據，因為有的同學長期低消費并不是由于經濟困難造成的，而真正困難的同學日常消費也是很低的，所以，必須依據低成本變量對數據做出調整。按表 2方法將低成本變量從定性分析轉換為定量計算。

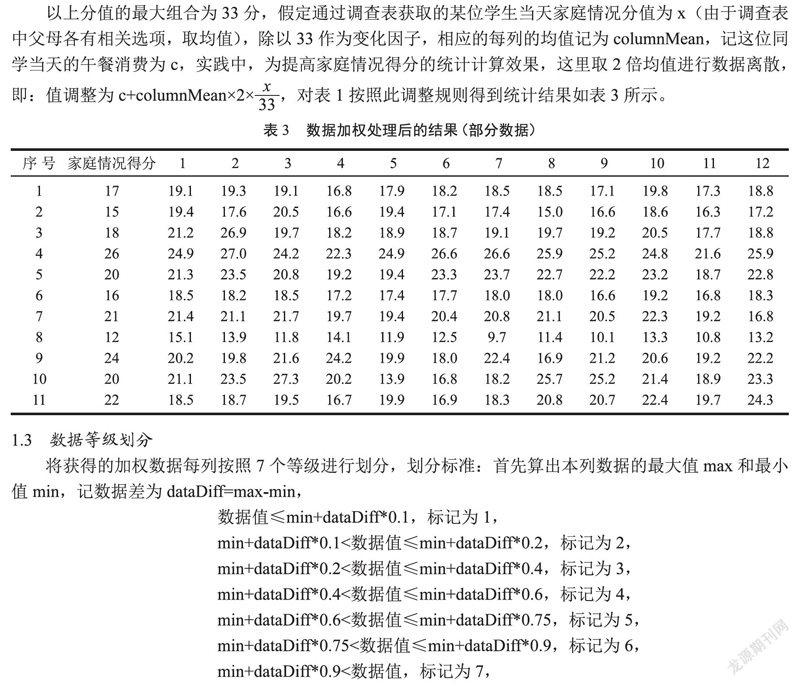
以上分值的最大組合為33分，假定通過調查表獲取的某位學生當天家庭情況分值為x（由于調查表中父母各有相關選項，取均值），除以33作為變化因子，相應的每列的均值記為columnMean，記這位同學當天的午餐消費為c，實踐中，為提高家庭情況得分的統計計算效果，這里取2倍均值進行數據離散，即：值調整為 c+columnMean€？€祝員？按照此調整規則得到統計結果如表 3所示。

1.3? ? 數據等級劃分

將獲得的加權數據每列按照7個等級進行劃分，劃分標準：首先算出本列數據的最大值max和最小值min，記數據差為dataDiff=max-min，

數據值≤min+dataDiff*0.1，標記為1，

min+dataDiff*0.1<數據值≤min+dataDiff*0.2，標記為2，

min+dataDiff*0.2<數據值≤min+dataDiff*0.4，標記為3，

min+dataDiff*0.4<數據值≤min+dataDiff*0.6，標記為4，

min+dataDiff*0.6<數據值≤min+dataDiff*0.75，標記為5，

min+dataDiff*0.75<數據值≤min+dataDiff*0.9，標記為6，

min+dataDiff*0.9<數據值，標記為7，

為了使得數據較為均勻的排列，max值的獲取并不都是按照最大值進行的，有時候會取第二大或第三大值作為max值，以本列中從1到7所有數字都出現為準則，比如：上述午餐消費表中的第4列最大值是37，如果以這個值為最大值，那么標識后的數據絕大多數都在1到3之間，5、6不出現，4也出現的很少，所以在這種情況下，以第二大數值26.8作為本列的最大值，當然按照這個處理規則，有的列中會多次出現7。按照上述規則，得到如表 4所示的學生午餐消費分段數據（每行代表1位同學，列是時間順序）。

2? ? 算法模型

2.1? ? 模型參數

2.3? ? 初始參數的確立

無論是EM算法還是HMM算法都是局部收斂，通常的做法是為每位同學隨機設定初始參數，然后進行循環迭代，通過python的HmmLearn包，或者matlab自帶的HMM統計工具箱進行測試，結果都不如人意，也就是說，僅僅依賴算法本身是沒有辦法獲取全局最優值的，在通過學生的午餐消費記錄估算學生經濟狀況時，采取了以下辦法，盡量保證算法結果與實際情況相符合，試驗證明，這種構造初始矩陣的方法是符合實際情況的。

1）狀態轉換矩陣A的確立

先統計每行中1到7出現的次數，然后以1出現次數+2出現次數+3出現次數的最大值作為極貧確認的依據，以2出現次數+3出現次數+4出現次數的最大值作為“比較貧困”的參考依據，依次類推，以5出現次數+6出現次數+7出現次數的最大值作為“富裕”的初步參考依據，統計結果如表 5所示。

依據上面定義規則，采用百分比形式，直接計算極貧百分比，即按照如下公式進行極貧百分比計算：

并根據數據表4的數據分段結果，依據k-means算法進行五類聚類，結果進行排序，得到如表 6所示排序結果。

根據上述排序結果，以8號同學作為極貧行，以作為A初始矩陣第1行的“極貧”概率，以作為A初始矩陣第1行的“較貧”初始概率，依此類推，以作為A初始矩陣第1行的“富裕”狀態的起始概率，依此類推，15號、17號、23號3位同學的分段統計結果的均值百分比，作為A初始矩陣第2行的各個概率，以10號、11號、28號、30號4位同學的分段統計結果的均值百分比，作為A初始矩陣的第3行的各個概率，以12號、32號、7號及3號4位同學的分段統計結果的均值百分比，作為A初始矩陣的第4行的各個概率，以4號，5號，26號3位同學的分段統計結果的均值百分比，作為A初始矩陣的第5行的各個概率，以得到完整的A初始矩陣。這里直接按照python程序中的格式給出結果（np為引入的numpy的別名）。

2）發射矩陣B的確定

仍然按照上述A初始矩陣選定的各行，按照表4分別計算分段結果1到7所占的比例作為B的各行，得到B初始值如公式 2所示。

3）初始狀態矩陣 確定

的確定按照傾向于貧困生的原則給出。

每位同學都以上述3個參數作為初始參數，在迭代過程中因為使用了前向和后向概率at（i）和 t（i）采用遞歸算法以后，前向變量和后向變量均小于1，此時會出現2個變量越來越小并迅速趨向于0的情況，預算中就有可能出現0/0情況，采取添加比例系數的辦法，避免出現0/0情況發生[10]。

3? ? 算法實現與結果的對比分析

3.1? ? 迭代結果分析

本項目的運行環境為：win7，64位OS，inter Core i5-6500處理器，主頻3.20GHz，Python3.5.3，自編軟件。根據上述初始參數 、A、B，對每位同學按照最大循環次數5000及閾值1e-9進行循環迭代，并最終按照期望值百分比即：

因為要按照極貧狀態由高到低進行排序，這里取i=1，得到結果如表 7所示。

按照20%資助對象進行分析，那么8號、7號、17號、19號、15號、24號、35號、5號這8位同學可以列為資助對象，但是將此數據與實際資助對象進行對比發現，8位同學中有2位同學是與實際調查結果不符合的，即：第7號同學和第5號同學。迭代算法對“極貧”8號同學的判斷是準確的，也就是說，實際的準確率只有75%。

3.2? ? HMM迭代結果與直接計算結果對比

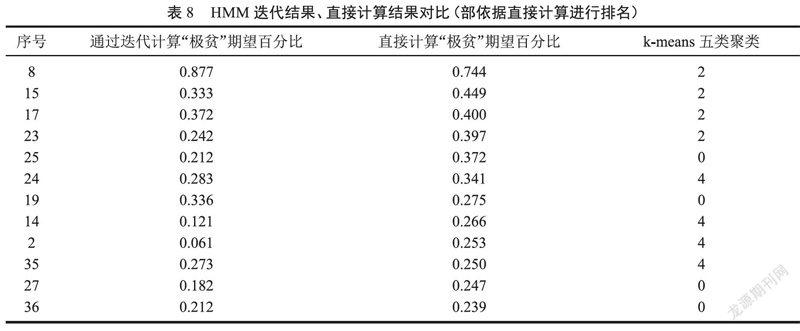
HMM的Baum-walch迭代結果、直接計算結果以及K-MEANS聚類結果如表8所示，其中K-MEANS聚類選擇了5個類別進行了聚類。表 8是按照“貧困期望值百分比”由低到高的順序排列的。

將直接計算得到的排名結果和實際情況進行對比，發現，除了“極貧”同學被準確命中以外，其它7位同學也被準確命中，上面所說的誤判的7號和5號同學都不在前11位。

如果僅僅對比HMM算法結果和直接計算的排名結果，可以發現，按照可以對20%的學生進行資助，那么取前8名，2種結果相差2位同學，通過和班主任實際情況核實，發現：HMM的計算結果的準確性不如直接計算。也就是說，我們采取了很多辦法希望保證HMM的準確性，但是與實際調查結果分析進行對比只能保證75%的準確率。而最簡單的直接計算反而可以保證幾乎100%的成功率。但是當資助比例降為10%～15%時，兩者的交集則比較準確。這個結果到底是一種必然現象還是一種偶然現象，3.3節對另外兩個班級應用上述方法進行驗證。

3.3? ? 另外班級的驗證

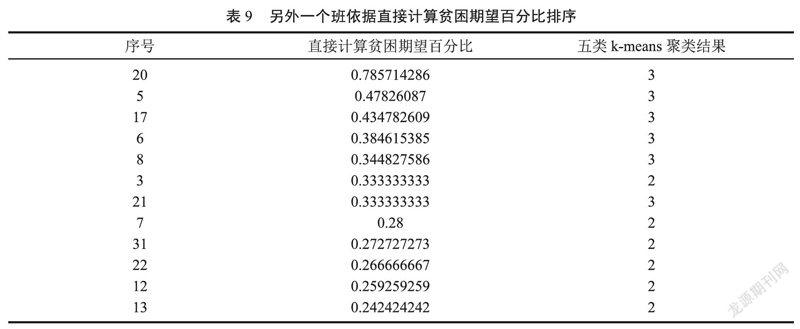
抽取另外1個班的連續11次午餐消費及家庭情況調查表，按照上面的數據加權處理、數據分段、統計、k-means聚類、構造初始矩陣、迭代，依據直接計算的排序結果如表 9所示。

對比依據Baum-welch迭代算法得到的概率期望計算的期望百分比，如表10所示。

依據Baum-welch迭代算法得到的結果，再求其“極貧”期望百分比，得到的結果由大到小排序后，原先依直接計算得到的結果中，2條記錄為新加，將2種結果提交班主任辨別，結論仍然是依據直接計算的結果更為可靠，二者都能正確地識別出“極貧”的第1位同學，在“貧困”名單中，前10名中仍然有2名差異，也就是說HMM的Baum-welch迭代算法的準確率，在這里達到了75%，而直接計算的結果反而得到班主任的認同。但是，如果資助比例降低為10%～15%，則也是兩者的交集更為可信。

由于篇幅的原因，另外一個班級數據不再列出，但結論是相似的，也就是說通過上述步驟進行的HMM的Baum-welch迭代算法的準確率大概在75%左右，如果資助比例降低，則二者的交集更為可靠。

4? ? 結論

復雜的HMM的Baum-welch算法得到的結論其準確性不如前期數據處理過程中直接使用數據分段統計結果得到的結論可靠。但二者對于“極貧”同學的判斷是一致的，不過，在實際工作中，因為資助比例沒有一個嚴格的限制，由此，我們給出高校貧困生認定的判別模型（按照10%最終資助比例）：

1）獲取原始的午餐消費記錄;

2）依據低成本變量并用2倍的當天消費均值對數據進行加權處理;

3）對加權處理后的數據進行分段，并進行分段統計（求和）;

4）直接依據分段求和結果進行貧困百分比計算，并進行五類的k-means聚類;

5）依據聚類結果設置HMM的Baum-welch算法的初始迭代參數;

6）根據迭代結果求直接計算和迭代結果的交集。

模型中依據外部低成本變量的2倍加權數據處理，也是在實踐中通過1倍到3倍、4倍等多種加權比較后得出的結論。從實踐效果來看，2倍數據加權效果最好。數據的多倍加權本質上是對外部低成本變量在算法中的權值進行調整。過高的權值會導致數據向高和低兩側集中，不利于數據等級的劃分，也將導致結果出現較大偏離。

參考文獻

[1]田志磊.采用非收入變量認定高校家庭經濟困難學生的實證研究[J].北京大學教育評論，2010，8（2）：146-147.

[2]胡苗苗.基于多屬性決策的高校家庭經濟困難學生認定方法及應用[J].重慶工商大學學報（自然科學版），2016，33（2）：54-57.

[3]何源.基于數據挖掘的高校貧困生輔助辨識系統設計[J].鄂州大學學報，2015，22（10）：106-109.

[4]周皞.基于校園卡數據挖掘的高校貧困生輔助判別研究[J].職教通訊，2012（35）：59-61.

[5]楊知玲.數據挖掘在高校貧困生評價中的應用[J].軟件導報，2016，15（6）：170-172.

[6]伊鵬.基于HMM的動態社會網絡社團發現算法[J].計算機研究與發展，2017，54（11）：2611-2612.

[7]李昕.基于改進的隱馬爾科夫模型的情感壓力分級方法[J].生物醫學工程學雜志，2016，33（3）：555-556.

[8]劉樹偉.基于時變隱馬爾可夫模型的機器人故障預測[J].機電一體化， 2016（6）：4-5.

[9]楊安駒，楊云.基于隱馬爾科夫模型的融合推薦算法[J].計算機與現代化，2015（9）：61-62.

[10]張天雄.基于HMM的通信流量異常檢測[J].智能計算機與應用，2018，8（4）：122-123.