飛行器級間段跨聲速脈動壓力特性試驗

武利龍，操小龍，王靖，周丹杰，羅金玲

1.北京機電工程研究所，北京 100074 2.北京空天技術研究所，北京 100074

錐柱外形作為航天類飛行器的一種常用外形，在跨聲速飛行時由于級間錐柱段的膨脹加速會在連接艙后的肩部區域達到局部超聲速產生激波，進而產生較強的壓力脈動，該壓力直接作用在飛行器表面會導致局部大載荷、誘導抖振響應進而導致結構破壞，從而大大縮短飛行器使用壽命；此外，脈動壓力還會造成嚴重的氣動噪聲，影響飛行器內部儀器正常工作。因此，開展錐柱外形飛行器的跨聲速脈動壓力特性研究對工程設計十分必要。

國內外對于此類飛行器外表面脈動壓力的研究始于20世紀60年代，Robertson[1]最早通過風洞試驗研究給出了錐柱體外形飛行器的靜態和動態壓力分布，揭示了產生動態壓力的非穩態流動機理。徐立功和劉振寰[2]分析了機動再入飛行器表面脈動壓力環境，并根據高超聲速無黏流計算的表面壓力分布，給出了一套預測脈動壓力環境統計特性的工程計算公式。Lananelli和Wolfer[3]給出了一套脈動壓力和功率譜的預測方法，適用于零壓梯度附體流和光滑、粗糙壁面上分離湍流邊界層流動。黃岬嵋和王劍[4]描述了飛機加改裝部件繞流的典型流態及脈動壓力。孟德虹等[5]通過數值模擬方法研究了某型戰斗機垂尾的脈動壓力特性。陳偉芳等[6]基于超聲速和高超聲速流動再入體表面的壓力分布給出了一套預測表面脈動壓力分布的工程方法，研究了馬赫數Ma、迎角、壁面溫度等因素對再入體表面脈動壓力環境的影響。Kumar等[7]通過試驗研究了火箭等錐柱外形跨聲速飛行時尾錐處的脈動壓力，分析了不同的尾錐角度和內外徑比對脈動壓力的影響規律。龍萬花等[8]利用平均流場的數值模擬與基于實驗的工程預測相結合的方法對跨聲速下旋成體的表面脈動壓力環境進行了分析預測，給出了旋成體在不同迎角、不同Ma條件下表面脈動壓力系數和功率譜分布。洪杰等[9]通過CFX軟件分析了超聲速和高超聲速球頭錐-柱再入飛行器表面脈動壓力分布特性，給出了一套預測表面穩定壓力和脈動壓力環境的工程方法。王娜和高超[10]通過對彈體模型進行表面脈動壓力特性實驗研究，給出了在跨聲速、超聲速不同迎角條件下沿彈軸測點的脈動壓力系數、頻譜曲線以及相關性系數。操小龍等[11]通過風洞試驗研究對錐柱外形飛行器亞、跨、超聲速條件下的脈動壓力特性進行了分析，給出了脈動壓力系數和功率譜密度隨Ma和迎角的變化規律。任淑杰等[12]通過采用雷諾平均Navier-Stokes方程求解流場、非線性噪聲求解方程求解聲場相結合的技術途徑，給出了一種預示大型火箭結構脈動壓力環境的方法。此外，美國NASA蘭利研究中心等機構的研究人員[13-17]近年來針對火箭等錐柱外形飛行器的跨聲速脈動壓力環境開展了大量的地面試驗以及飛行試驗測量，并對兩者進行了對比分析。

通過上述國內外關于錐柱外形脈動壓力的研究可以看出，錐柱外形參數是影響局部脈動壓力量級的重要因素之一，然而關于不同錐角和錐長大小對脈動壓力影響規律的研究報道較少，同時，受制于早期傳感器尺寸以及頻響范圍的約束，相關試驗測量值相對較小。因此，本文通過試驗研究，開展錐角和錐長對錐柱外形飛行器跨聲速脈動壓力的影響規律研究，為航天類飛行器結構設計提供較好的支撐。

1 試驗模型及設備

本文研究的錐柱外形示意圖如圖1所示，試驗共選取了5種不同錐角模型，分別為10°、12.7°、15.3°、20°和25°。測點從肩部膨脹拐點后開始沿上母線依次布置，具體位置及編號如圖1所示。

為了分析錐長對脈動壓力的影響，固定錐角，本文選取了錐角θ=12.7°為研究基準，取原始縮比模型的錐長為l0，共選取了5種不同錐長l尺寸模型，其長度分別為l/l0=0.48、0.62、0.82、1.0、1.27，具體如圖2所示，其中li為第i種錐形艙段模型的長度，di為與第i種錐形艙段模型連接圓柱段的直徑。

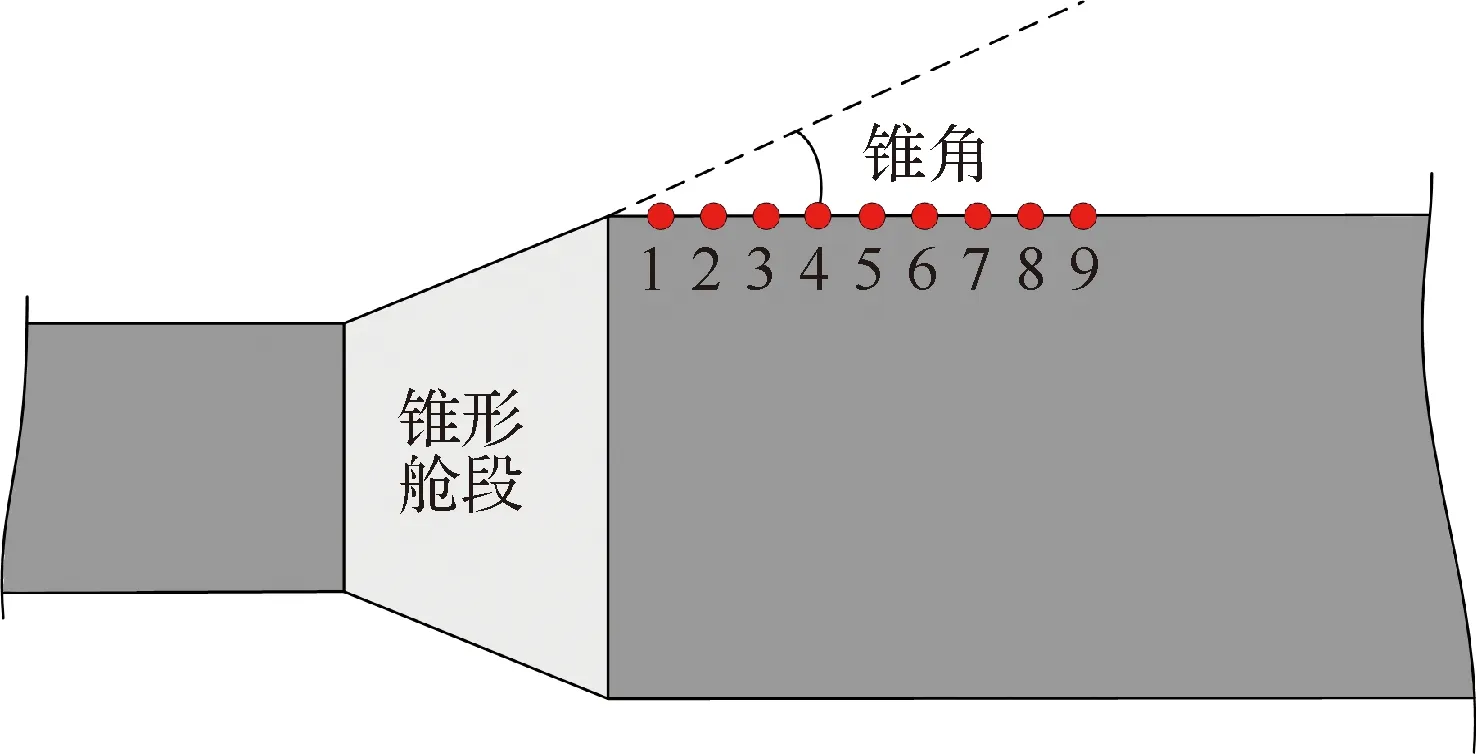
圖1 錐柱外形及測點位置Fig.1 Cone-cylinder configuration and position of measurement points

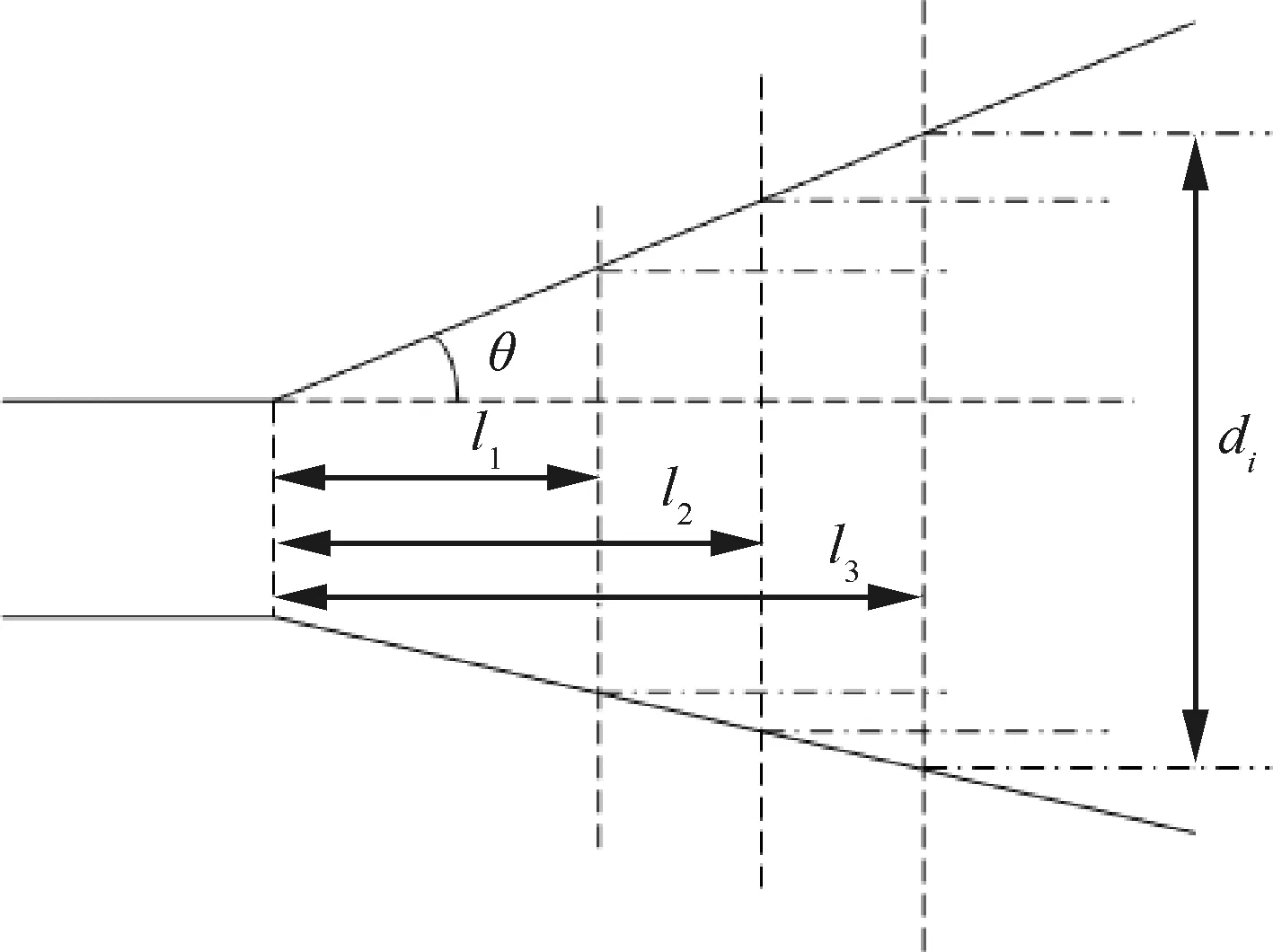
圖2 模型錐長變化示意圖Fig.2 Schematic diagram of models with different cone length

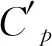
(1)

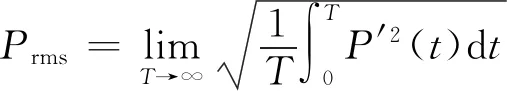
(2)

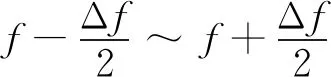
2 試驗結果及分析

各個錐角模型的試驗馬赫數范圍均為0.75～1.2，迎角均為0°。由于脈動壓力峰值對于自由來流馬赫數比較敏感，所以試驗測量馬赫數間隔取為0.01。

2.1 流動規律

對于如圖1所示的錐柱外形，當跨聲速氣流流過時，由于錐柱連接艙前端壓縮角和后端膨脹角的二次加速，錐柱體肩部后局部區域氣體流速會達到超聲速，在肩部后產生明顯的激波。試驗紋影如圖3所示，隨著Ma增大，肩部的激波影響區域逐漸加大，并沿著軸向向后推移，在肩部區域形成了明顯的斜激波和正激波，呈現出λ形，并且該激波表現出不穩定特性，在肩部區域出現明顯的振蕩現象。此外，對于較大錐角情形由于物面外折在肩部區域還會伴隨有流動分離，分離后再附區域會形成再壓縮激波，激波與邊界層干擾會進一步誘導流動分離。正是由于局部激波、流動分離以及邊界層等復雜流動的相互干擾在肩部區域產生了強烈的脈動壓力現象，試驗的所有模型，隨著來流Ma的增加均在肩部出現了上述的激波及振蕩現象，并表現出了較強的脈動壓力，但不同級間段模型量值上出現了較大的差異。

圖3 跨聲速肩部區域流動紋影圖片Fig.3 Schlieren flow-visualization pictures on shoulder region at transonic speed

2.2 不同錐角結果

對5種不同錐角模型肩部測點數據進行處理分析，沿上母線各個測點處脈動壓力系數隨Ma的變化規律，如圖4所示，其中各個測點的脈動壓力系數均采用最大峰值進行了歸一化，后述結果處理方式相同。可以看出，5個錐角模型的脈動壓力系數峰值均出現在肩部區域的前4個測點位置，其中距離肩部0.05d和0.15d(d為錐形艙段后端圓柱的直徑)的1和2號位置處最為嚴酷。結合流動紋影以及圖5所示最大和最小錐角模型在測點1處的功率譜密度(PSD)分布可以得出，嚴酷的脈動壓力主要是由于肩部不穩定的激波振蕩所致，并且從圖中可以看出在頻率f=100 Hz左右出現了明顯的以低頻為主導的能量集中區域。此外，通過分析各個測點峰值及對應的Ma可以看出，肩部的激波隨著Ma的增加在不斷后移，并且激波的強度在不斷減弱，在距離肩部0.35d的4號測點處其脈動壓力系數已降至最大峰值的50%左右，繼續向后會進一步減小。

提取不同錐角模型肩部1、2號測點的脈動壓力系數峰值隨Ma的變化結果，具體對比如圖6所示，可以看出，1號測點的脈動壓力峰值主要集中在Ma=0.81～0.86范圍內，而2號測點主要集中在Ma=0.87～0.92之間。對于各測點的脈動壓力峰值僅在很窄的Ma區間內出現，隨著激波的推移會迅速減小。將各個錐角模型的脈動壓力系數最大值進行對比分析，結果如圖7所示，可以看出隨著錐角增加脈動壓力系數先表現出平緩增加，當錐角大于15°時，Cp′增加幅度進一步加大，錐角從10°變化至25°脈動壓力系數峰值增大了將近一倍。

2.3 不同錐長結果

對于不同錐長模型，沿上母線分別選取肩部前4個測點，即測點1、2、3和4，分析錐長對脈動壓力的影響規律。圖8為上述4個監測點處的脈動壓力系數隨著錐長和Ma的變化結果。從圖8(a)測點1處結果中可以看出，錐長比l/l0為1.27的模型首先在Ma=0.809處達到峰值，隨著錐長的減小，各個模型達到峰值的Ma在增大，對于l/l0=0.48的模型在Ma=0.903處才達到峰值，并且各個模型的Cp′峰值結果比較接近。對于圖8(b)測點2結果，同樣可以看出隨著錐長的減小，各個模型達到峰值的Ma在增大，但最短的l/l0=0.48模型的峰值明顯小于其他4種情形，即沿流向從測點1到測點2錐長最小模型的脈動壓力系數峰值首先出現了較大幅度的減小。結合該模型在測點1處Cp′峰值出現的Ma最大，說明錐長最短的模型僅在很窄的Ma區間出現脈動壓力峰值，并且在肩部的作用區域很小。

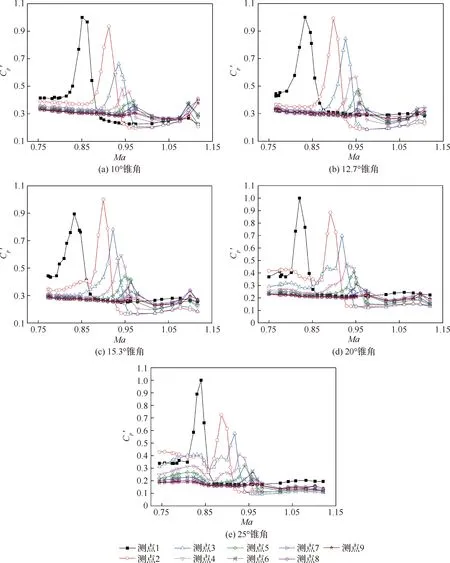
圖4 5種錐角模型肩部區域脈動壓力系數隨馬赫數的變化Fig.4 Variation of fluctuating pressure coefficient with Mach number for five cone angle configurations

進一步對測點3、4進行分析，結果分別如圖8(c)和圖8(d)所示。從測點3的結果可以看出，錐長比l/l0=0.62的模型Cp′峰值出現了大幅減小，為最長模型的55%；同時l/l0=0.82模型也出現了一定幅度的減小，其峰值為最長模型峰值的78%。對于圖8(d)所示的測點4結果，可以看出l/l0=0.48，0.62，0.82，1.0，這4個模型的Cp′峰值均出現了進一步的驟減，其中前3個較短模型的峰值分別為最長模型的48%、53%和58%，而次長模型也僅為最長模型峰值的69%。

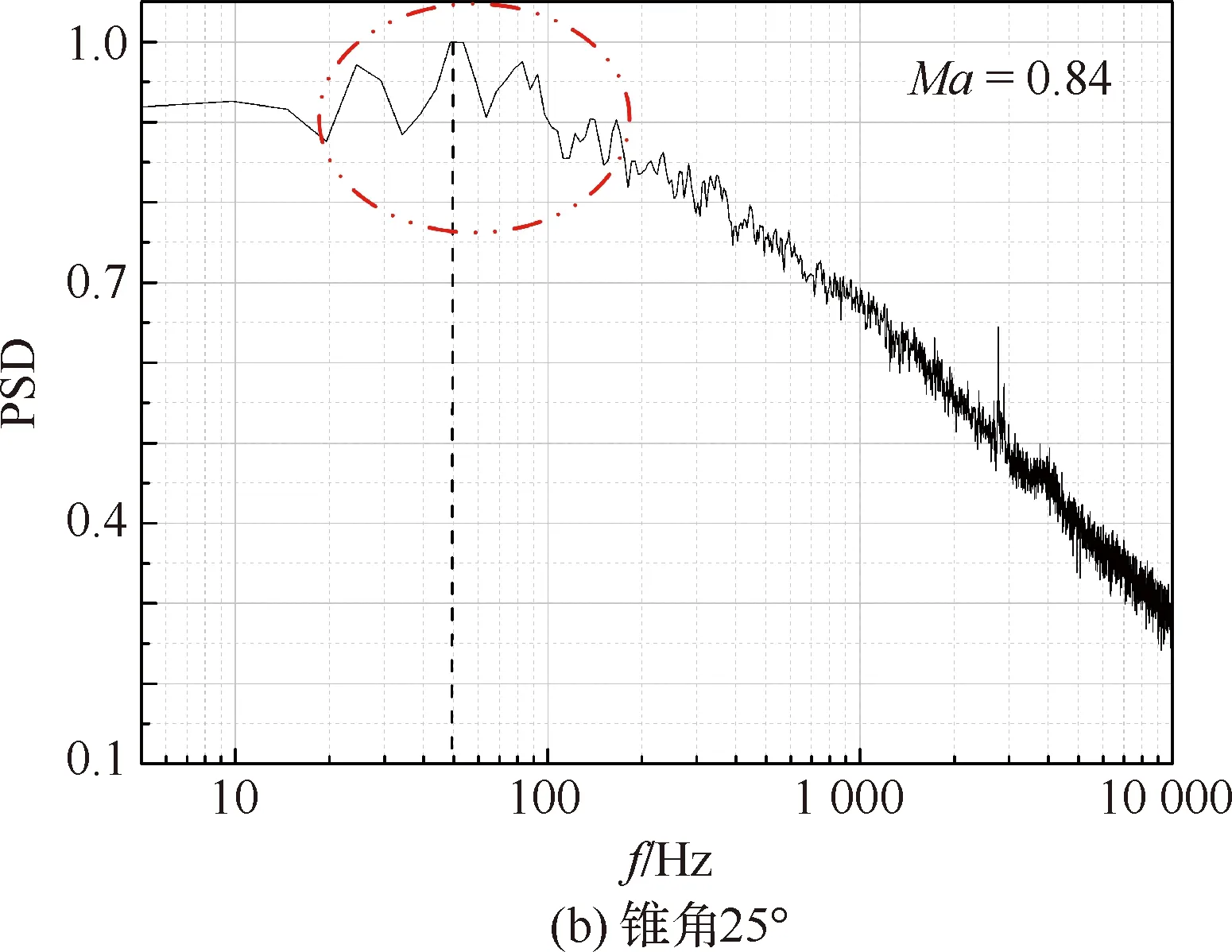
圖5 兩種錐角模型測點1處的功率譜密度分布Fig.5 Power spectral density of two cone angle configurations at Point 1

通過上述結果分析可以看出，隨著錐柱連接段越長，上母線肩部區域的脈動壓力作用范圍越大，同時在該作用區域脈動壓力峰值維持的Ma區間也越寬；該結果進一步表明錐柱級間段越長，氣流加速越大、激波也越強，當其縮短到一定長度時，肩部區域的脈動壓力峰值基本消失。

選取最短和最長兩個模型肩部測點1做功率譜密度分析，結果如圖9所示，可以看出在頻率為100 Hz以內的窄帶區間同樣出現了較為明顯的能量集中區域，說明肩部脈動壓力峰值同樣為低頻的不穩定激波振蕩所致。

此外，對比5種不同錐長模型的脈動壓力系數最大值可以發現，結果量值接近，具體如圖10所示，從而可以說明錐長對脈動壓力局部峰值的大小幾乎沒有影響，影響的只是Cp′峰值出現的敏感Ma大小以及肩部區域作用的范圍大小。

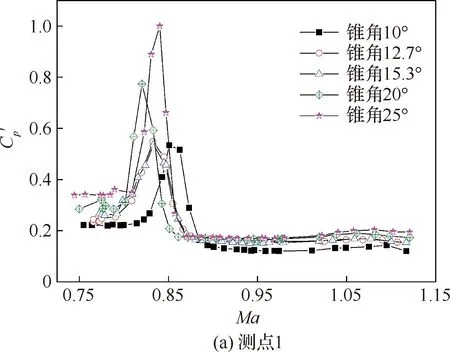
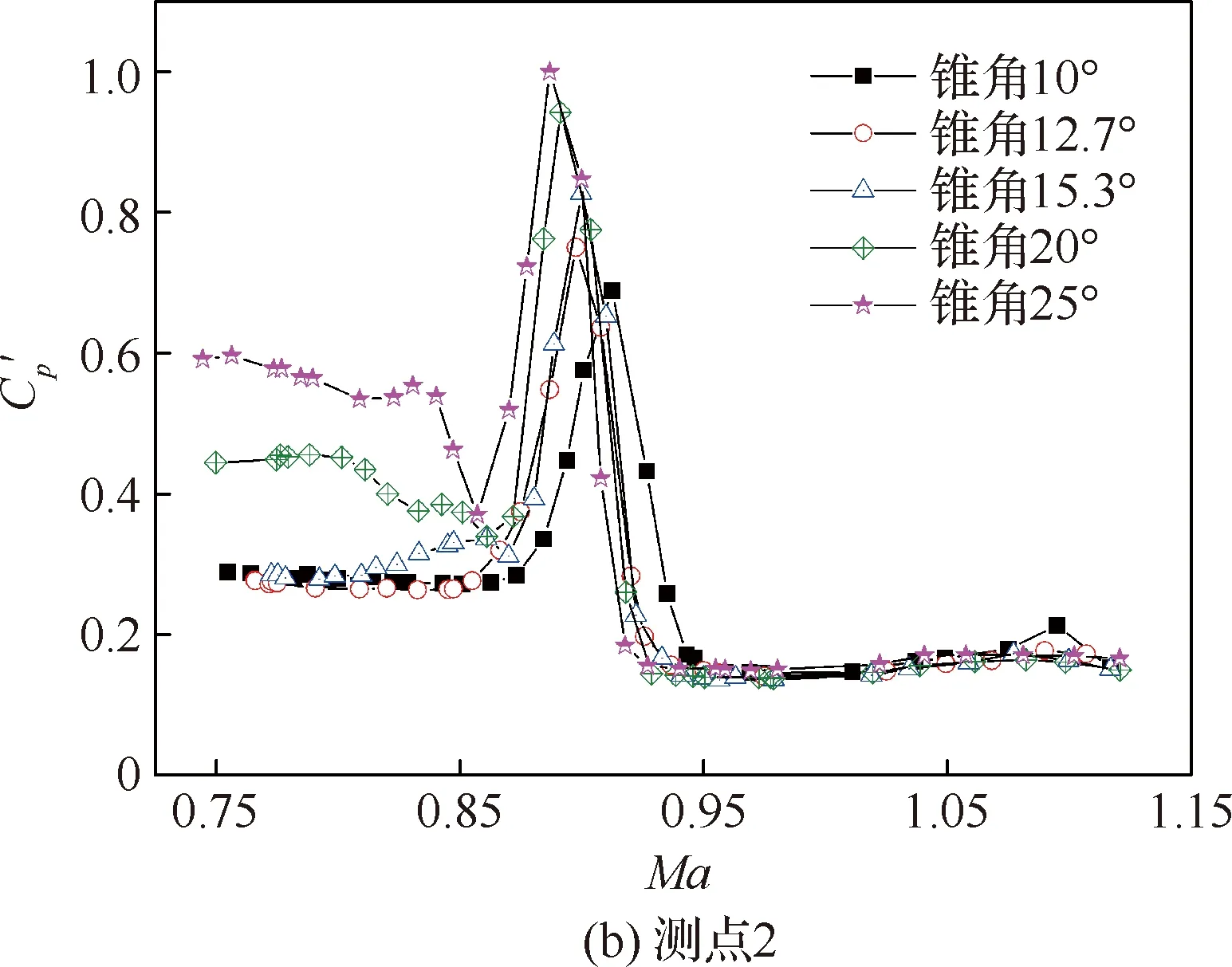
圖6 測點1、2處Cp′隨錐角和Ma的變化Fig.6 Variation of Cp′ with cone angle and Ma at Point 1 and Point 2

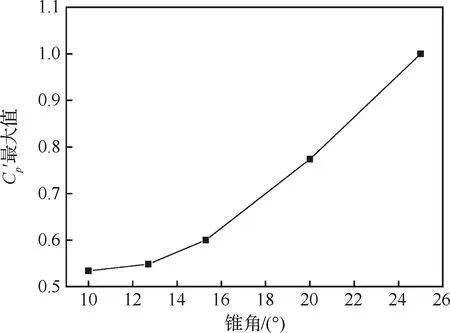
圖7 脈動壓力系數最大值隨錐角的變化規律Fig.7 Variation of the maximum of fluctuating pressure coefficient with cone angle

3 結 論

本文通過脈動壓力風洞試驗測量的方法，對比分析了不同錐角和錐長大小對錐柱外形飛行器跨聲速(Ma=0.75～1.2)脈動壓力的影響規律，結論如下：

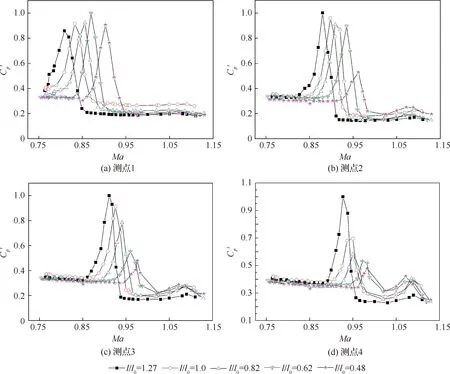
圖8 不同測點Cp′隨錐長比和Ma的變化規律Fig.8 Variation of Cp′ with cone length ratio and Mach number at different measuring points

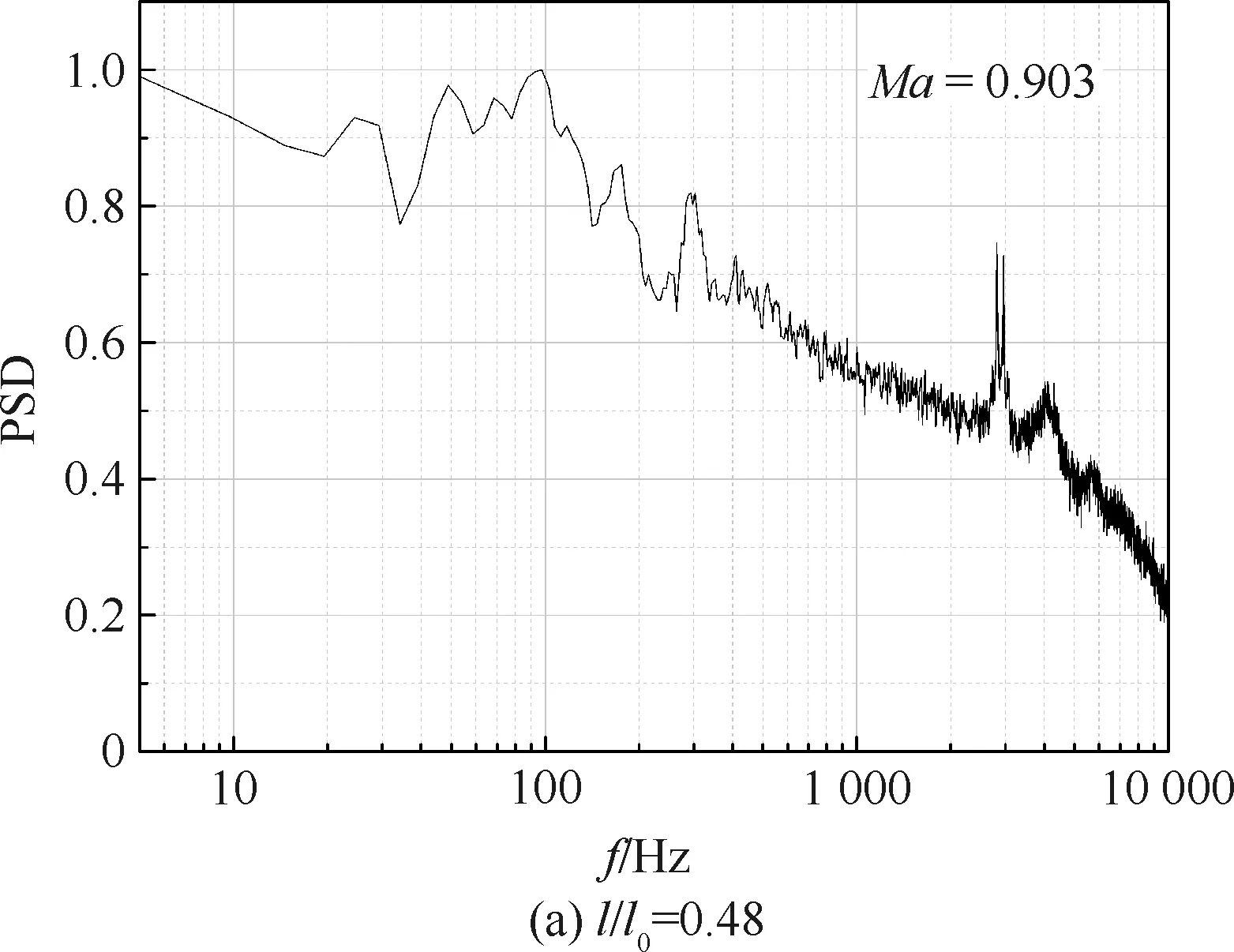
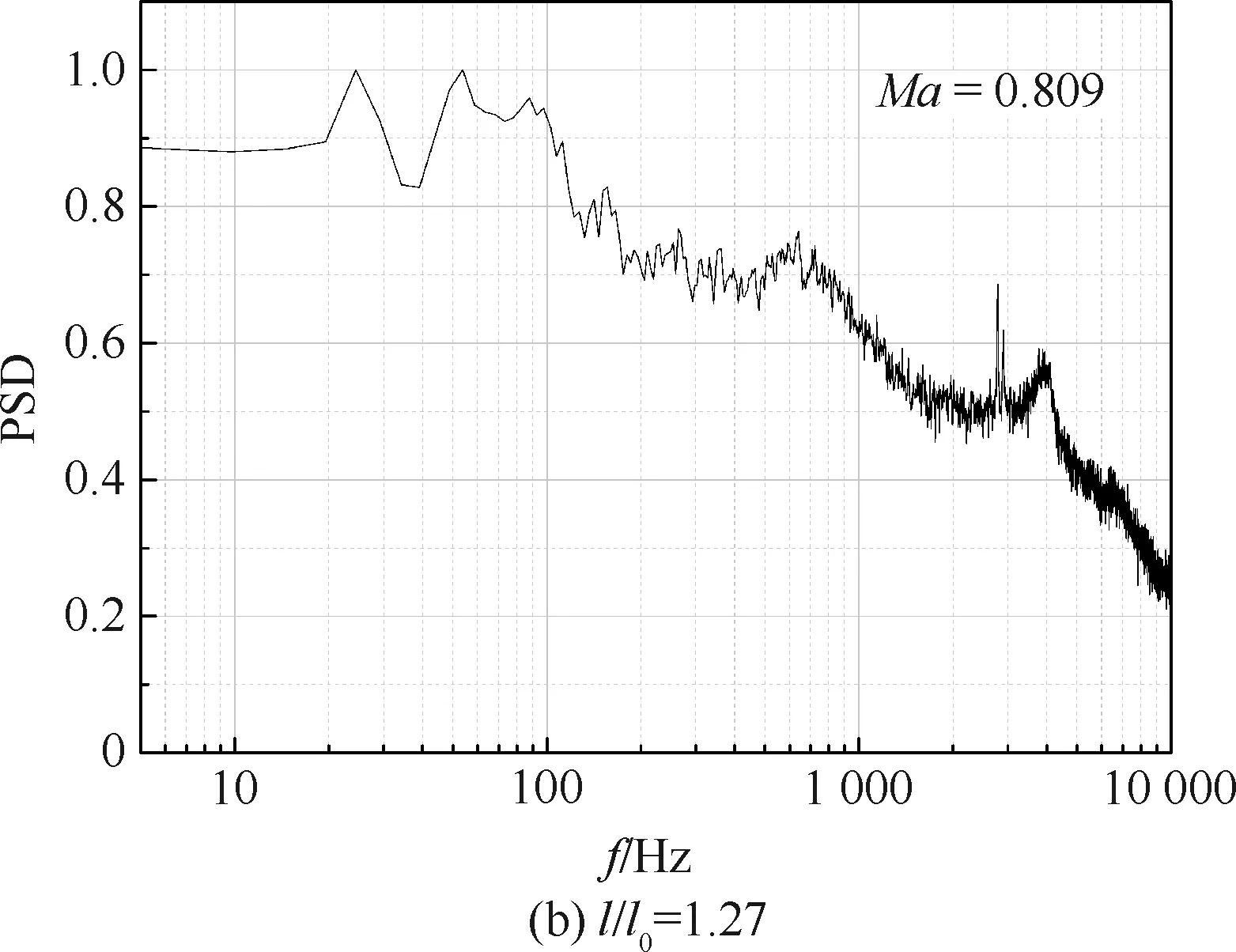
圖9 兩種不同錐長模型測點1處的功率譜密度分布Fig.9 Power spectral density of two cone length configurations at Point 1

1)對于級間段為錐柱外形設計的飛行器，在跨聲速飛行時肩部區域會出現較強的脈動壓力。

2)對比分析5種不同的錐角模型，錐角大小分別為10°、12.7°、15.3°、20°和25°，肩部區域的脈動壓力峰值均呈現隨Ma增加先增大后減小的趨勢，并且峰值僅在很窄的Ma區間內出現，隨著肩部激波的后移會迅速減小；此外，所有模型的跨聲速脈動壓力峰值均作用在肩部拐點后1.0d的范圍內，其中較為嚴酷區域位于0.35d的區域范圍，且最大峰值隨著錐角的增加表現出，當其小于15°時先平緩增加，隨著錐角進一步增大，Cp′增加幅度進一步加大。

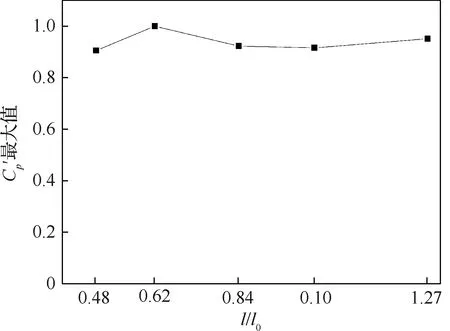
圖10 脈動壓力系數最大值隨錐長比的變化規律Fig.10 Variation of maximum Cp′ with cone length ratio

3)對于相同錐角、不同錐長的模型，級間段越長，脈動壓力在肩部區域的作用范圍會越大，同時在該作用區域脈動壓力峰值維持的Ma區間也會越寬；對比5種不同錐長模型的脈動壓力系數最大值，可以看出其結果接近，進一步表明影響最大值的關鍵參數為錐角大小。

4)對峰值點脈動壓力的功率譜密度分析結果表明，以低頻為主導的窄帶區間能量較為突出，其主要集中在100 Hz左右，進一步表明嚴酷的脈動壓力主要是由于肩部不穩定的激波振蕩所致。

綜合整個試驗結果，其規律性較好，對于飛行器設計具有重要的支撐作用。