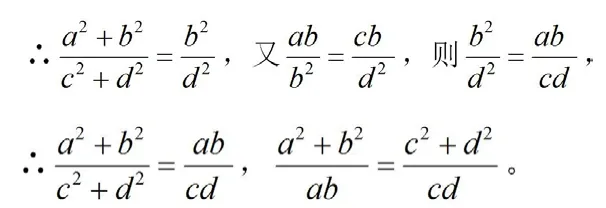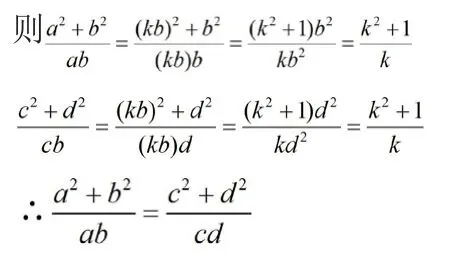初中數學解題思維的探究

應素娜

（浙江省寧海縣桃源中學，浙江 寧海 315600）

一個好的數學題，常常是培養能力的好素材，許多問題教師如能分析引導得法，就能培養與提高學生的能力，因此一個數學教師如果經常性地給學生以適合他們的程度的問題去引導，并且用一些合適的方法來幫助他們鑰匙，就會引起學生們對獨立思考的興趣。本文是筆者經過研究與實踐，認為訓練與培養學生的解題能力可以從以下幾個方面著手：

一、培養學生能正確、迅速、靈活地運用解題模式與典范解法的能力

對各種類型數學問題及其解法進行細致剖析，提煉出它的本質特征，總結各種數學解題的模式和典型解法，讓學生模仿、實踐是提高學生解題能力的有效途徑。在幾何證明中證明兩條線段之和等于第三條線段時，常常采用“截長補短”的方法，而在遇到有關中線問題時，常用到“加倍法”或“減半法”等都有其典范性。

例1：如圖1已知AD//BC，∠1＝∠2，∠3＝∠4。直線DC過E點交AD于D，交BC于C。

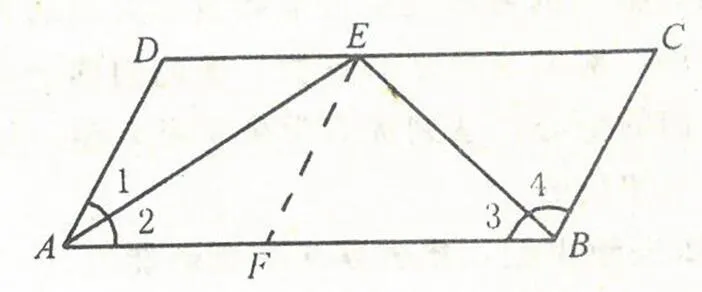
（圖1）

求證：AD+BC＝AB

分析：如果在AB上截取AF，使AF＝AD，那么，只需證明BF＝BC即可，這就轉化為證明兩條線段相等的問題，可考慮證△BFE≌△BCE。

二、培養學生善于分析，變換問題的能力

教師在分析一道題目后，如果能適當地變換一下問題的條件或結論，則可能得到新題目，并引導學生尋找出其中有規律的東西，可以起到舉一反三的作用。

例2：已知三點，求解析式，一般情況下用它的一般式y＝ax2+bx+c(a≠0)較方便

拋物線經過(2, 0)，(0,-2)，(-2, 3)三點

解：設二次函數解析式為：y＝ax2+bx+c 由題意得

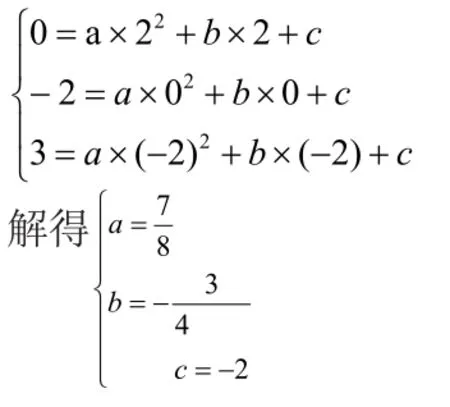
三、培養學生善于把一個問題轉化成一種等價的簡單形式，抓住一個問題的核心的能力

有時為了探索問題的解決途徑，常要改變問題的形式，使探索易于進行，這就是轉化。換句話說，我們發現所給的問題屬于我們不熟悉的類型，對于這種類型我們不知道解它的一般方法，那么我們下一步應該怎么做呢？只有設法轉化為熟悉的，以前解過的問題，當然關于這種轉化不熟悉的問題為熟悉的問題。并沒有一定的規律，但是，如果教會學生留意觀察所有那些用來找出了解決問題的辦法，那么學生就會逐漸地形成這種轉化的能力。

例3：若方程x2+(m-2)x+(5-m)=0的兩根都比2大。求實數m的范圍。

分析：方程x2+(m-2)x+(5-m)=0的兩根都比2大的圖形有下列兩種情況：[記f(x)=x2+(m-2)x+(5-m)]。

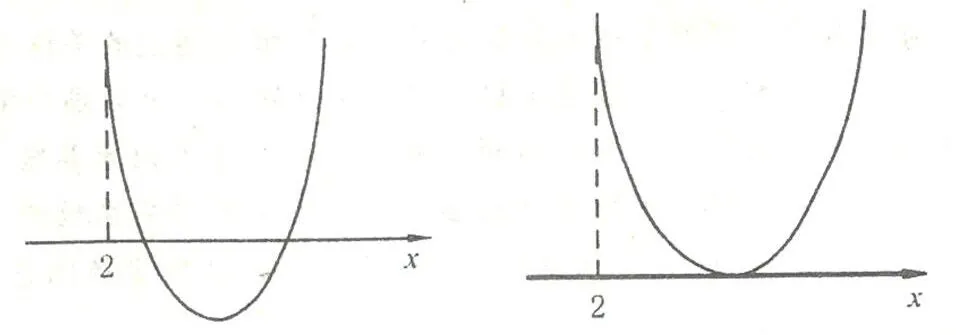
同樣地，我們可引導學生總結出一元二次方程ax2+bx+c=0的“兩根都在α與β之間(α<β)”或“兩根至少有一個在α與β之間(α<β)”或“兩根至多有一根為負”的等價條件。

四、培養學生多角度，多方位思考問題的能力

解題是一種創造性思維活動，僅僅具有扎實的基礎知識和基本技能還是不夠的，教師應引導學生善于從不同角度、不同方位思考問題，探索解題思路；引導學生主動地、最大限度地搜集有助于解題的各種信息、充分利用已知條件，挖掘對解題有用的隱含條件；引導學生回想與問題直接有關的數學知識、數學方法以及曾經解過的數學問題；從中使學生獲得從聯想中尋找與熟悉相似的問題。以及與問題接近的數學知識，運用這些知識來提高解題的能力。

分析：此題可引導學生考慮運用比例性質，也可采用一般連等式常用的比值為k，于是得到：