一個數(shù)學游戲的一點探討

蔣金團

（云南省保山市施甸縣第一完全中學，云南 保山 678200）

一、問題的描述

在美國，曾經(jīng)流行過這樣一個數(shù)學游戲。這個游戲的規(guī)則十分簡單，任意寫出一個自然數(shù)N，如果是個奇數(shù)，則下一步變換成3N+1；如果是個偶數(shù)，則下一步變換成N/2。得到第一個結果之后，按照規(guī)則重復運算，則無論N是怎樣一個數(shù)字，最終無法逃出落入底部的4-2-1-4循環(huán)。這就是著名的“冰雹猜想”，在亞洲也被稱作稱角谷猜想。

二、問題的分解

（一）放大倍數(shù)

1.“3N+1”與倍數(shù)的關系

對于任意奇數(shù)N,根據(jù)角谷變換規(guī)則,它的第一步將變?yōu)?N+1,此時放大了多少倍?

①當N=1時,倍數(shù)=4；②當N為大于1的奇數(shù)時,“乘3加1”變換相當于把奇數(shù)放大了三點幾倍.

（二）步數(shù)討論：任意自然數(shù)經(jīng)過多步角谷變換之后,能回到自身?

為了討論的方便,我們設起始數(shù)為偶數(shù).因為對奇數(shù)實施“乘3加1”變換時,它將變成偶數(shù),具體來說，尾數(shù)為1的每一個奇數(shù)都對應一個尾數(shù)為4的偶數(shù),尾數(shù)為3的每一個奇數(shù)都對應一個尾數(shù)為0的偶數(shù),尾數(shù)為5的每一個奇數(shù)都對應一個尾數(shù)為6的偶數(shù),尾數(shù)為7的每一個奇數(shù)都對應一個尾數(shù)為2的偶數(shù),尾數(shù)為7的每一個奇數(shù)都對應一個尾數(shù)為2的偶數(shù),只要證明偶數(shù)經(jīng)過多次角谷變換之后都后回到谷底1,則奇數(shù)同樣如此.

1.偶數(shù)經(jīng)過兩步變換能回到自身?

設X1為起始偶數(shù)項,X1要想回到自身,只能滿足放大倍數(shù)等于縮小倍數(shù),即解得因此沒有偶數(shù)經(jīng)過兩步變換能回到自身。

2.偶數(shù)經(jīng)過三步變換能回到自身?

設X1為起始偶數(shù)項,X1要想回到自身,只能滿足放大倍數(shù)等于縮小倍數(shù),所以流程中只能有兩次”除以2”變換和一次“乘3加1”變換,根據(jù)流程可列如下方程：

結論：在一切偶數(shù)中,只有2、4兩個數(shù)經(jīng)過三步變換能回到自身.

3.偶數(shù)經(jīng)過四步變換能回到自身?

四步變換只能是如下的組合：3次“除以2”變換和1次“乘3加1”變換；2次“除以2”變換和2次“乘3加1”變換；1次“除以2”變換和3次“乘3加”變換；顯然任意一種組合,都不可能滿足放大倍數(shù)等于縮小倍數(shù),所以一切自然數(shù)經(jīng)過四步變換都不可能回到自身,同理可討論一切自然數(shù)經(jīng)過5步變換都不可能回到自身.

4.偶數(shù)經(jīng)過六步及其以上的變換時,能回到自身?

當變換過程有六個步驟時,流程至少包含兩個“乘3加1”變換,否則放大倍數(shù)遠小于縮小倍數(shù),但是一旦出現(xiàn)兩次“乘3加1”變換,至少有一次的放大倍數(shù)為”三點幾倍”,出現(xiàn)小數(shù),而縮小倍數(shù)只能是偶數(shù),兩者不可能相等.所以一切偶數(shù)經(jīng)過六步及其以上變換時,都不可能回到自身.

綜上所述,“2、4”除外的一切偶數(shù)經(jīng)過角谷變換后都不能回到自身,無論變換過程有多少步；因此“1”除外的一切奇數(shù)經(jīng)過角谷變換后都不能回到自身,無論變換過程有多少步。即“1、2、4”除外的一切自然數(shù)經(jīng)過角谷變換都不能回到自身。

（三）討論變換特點

根據(jù)尾數(shù)，將自然數(shù)分成十行，每一行都是公差為10的等差數(shù)列，第一行的通項公式為10k1+1(k1=0、1、2、3、...）；第二行的通項公式為10k2+2(k2=0、1、2、3、...）；第三行的通項公式為10k3+3(k3=0、1、2、3、...）；第四行的通項公式為10k4+4(k4=0、1、2、3、...）；第五行的通項公式為10k5+5(k5=0、1、2、3、...）；第六行的通項公式為10k6+6(k6=0、1、2、3、...）；第七行的通項公式為10k7+7(k7=0、1、2、3、...）；第八行的通項公式為10k8+8(k8=0、1、2、3、...）；第九行的通項公式為10k9+9(k9=0、1、2、3、...），第十行的通項公式為10k10+10(k10=0、1、2、3、...）。

根據(jù)變換規(guī)則，對奇數(shù)實行“乘3加1”變換之后將變?yōu)榕紨?shù)，具體如下，第1行奇數(shù)將演變?yōu)榈?行偶數(shù)，第3行奇數(shù)將演變?yōu)榈?0行偶數(shù)，第5行奇數(shù)將演變?yōu)榈?行偶數(shù)，第7行奇數(shù)將演變?yōu)榈?行偶數(shù)，第9行奇數(shù)將演變?yōu)榈?行偶數(shù).

根據(jù)變換規(guī)則，對偶數(shù)實行“除以2變換”變換，相應的約束關系討論如下。

1.第2行偶數(shù)的變換特點

對第2行偶數(shù)實行“除以2”變換之后，有一半偶數(shù)轉變?yōu)榈?行奇數(shù)，另一半偶數(shù)轉變?yōu)榈?行偶數(shù)，相應的約束條件如下：

上述討論結果可用如下流程圖表示：

上述討論結果可用如下流程圖表示：

同理可討論其它行偶數(shù)除以2之后的變換特點和上述流程類似，最后可把各行變換組成如下網(wǎng)狀結構。

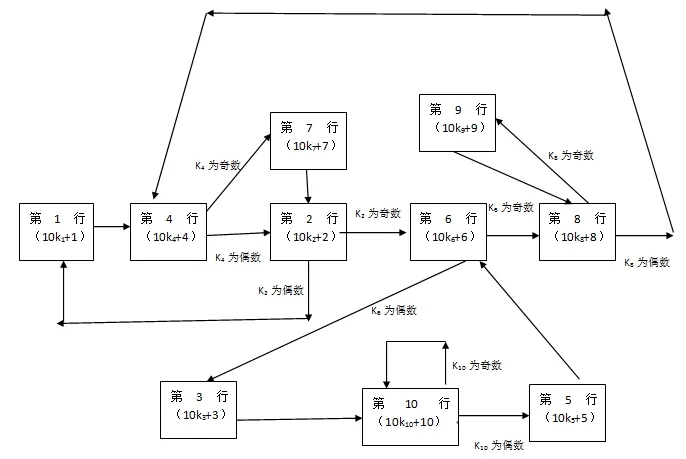
通過以上的網(wǎng)狀圖可以得出一個重要結論：當自然k數(shù)從某行演變?yōu)榱硗庖恍袝r，每碰到“除以2”變換一次，符合條件的k值數(shù)量都會在原來的基礎之上減少，同時每碰到“除以2”變換一次，符合條件的k值之間的間隔將增大，因為碰到“除以2”變換時，k值將會分成奇偶兩支。

三、問題的解決及相關的證明

為了討論方便，在上面的網(wǎng)狀圖中，我們將“第4行→第2行→第6行→第8行→第4行”這一路徑稱為主鏈。因為第4行的數(shù)值演變成第2行的數(shù)時，演變結果包含第2行的一切數(shù)值（2、12、22、32、42……）；第2行的數(shù)值演變成第6行時，演變結果包含第6行的一切數(shù)值（6、16、26、36、46……）；第6行的數(shù)值演變成第8行時，演變結果包含第8行的一切數(shù)值（8、18、28、38、48……）；第8行的數(shù)值演變成第4行時，演變結果包含第4行的一切數(shù)值（4、14、24、34、44……）。

假設有一個數(shù)能在路徑“第6行→第3行→第10行→第5行→第6行”之間不停循環(huán)，則將會有更多的數(shù)能在該環(huán)形圈里面循環(huán)，因為1、2 、4除外的自然數(shù)經(jīng)過角谷變換之后都回不到自身。這樣一來，在無窮次循環(huán)過程中，有一些滿足條件的數(shù)之間的距離將永遠保持不變。但另一方面，第6行的數(shù)經(jīng)“第6行→第3行→第10行→第5行→第6行”路徑再次回到第6行時，接下來是除以2變換，滿足條件的數(shù)都會減少，每循環(huán)一次，滿足條件的數(shù)就減少一次，即滿足條件的數(shù)與數(shù)之間的距離終會改變，這與前面的分析產(chǎn)生了矛盾,這說明前面的假設是錯誤的，因此沒有數(shù)能在路徑“第6行→第3行→第10行→第5行→第6行”之間永遠循環(huán)下去。用同樣的方法可以證明，沒有數(shù)能在路徑“第8行→第9行→第8行”之間無窮循環(huán)；也沒有數(shù)能在路徑“第1行→第4行(第7行)→第2行→1行”之間無窮循環(huán)(1、2、4三個數(shù)除外)。綜上所述，一個數(shù)最終沒有落入底部的“4-2-1-4”循環(huán)，則這個數(shù)將無數(shù)次經(jīng)過主鏈的每個節(jié)點，這樣來問題就好辦多了。

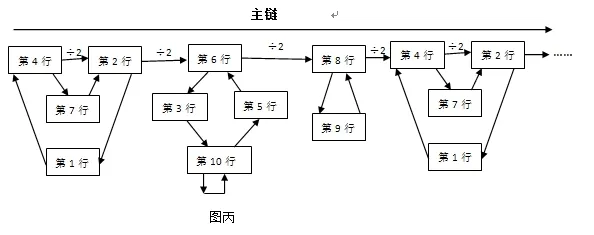
為討論的方便，我們設“第4行”的數(shù)為首項,如果有一個數(shù)沒有落入谷底1.則這個數(shù)將無數(shù)次演變成主鏈上的節(jié)點數(shù)，而節(jié)點數(shù)又可以看成是第4行的某個數(shù)沿著主鏈多次除以2得到的，因為變換可以無窮無盡持續(xù)下去，這就要求第4行中有一個數(shù)能沿著主鏈無窮變換下去（如圖丙所示）。

但從循環(huán)圈的角度講，第4行的某個數(shù)沿著主鏈無窮變換下去，實質上要求該數(shù)能在“第4行→第2行→第6行→第8行→第4行”循環(huán)圈里永遠變換下去，如圖丁所示。根據(jù)前面的結論，“1、2、4”除外的一切自然數(shù)經(jīng)過角谷變換都不能回到自身，因此第4行的某個數(shù)沿著圖丁所示的循環(huán)圈再次回到第4行時，它已經(jīng)變成第4行的另一個數(shù)，即只要有一個數(shù)能在圖丁所示的循環(huán)圈里面無窮循環(huán)，則將會有更多的數(shù)能在循環(huán)圈里面無窮循環(huán)，也就是說，在循環(huán)過程中，有一些滿足條件的數(shù)值，它們之間的間隔將保持不變。但事實上，第4行的所有數(shù)值沿著主鏈循環(huán)變換時，每碰到“除以2”變換一次，符合條件的數(shù)值就減少一次，滿足條件的那些數(shù)值之間的間隔終會改變，這與前面的分析產(chǎn)生了矛盾，因此前面的假設“如果有一個數(shù)沒有落入谷底1”是錯誤的，角谷猜想得證。