考慮粘彈性泊松比的固體推進劑蠕變型本構模型①

崔輝如，張 斌，申志彬，李海陽

(1.國防科技大學 空天科學學院，長沙 410073；2.中國航天科工集團有限公司第九總體設計部，武漢 430040)

0 引言

固體推進劑是典型的粘彈性材料，其泊松比在結構分析中扮演著重要的角色。試驗結果表明[1]，推進劑粘彈性泊松比是與時間、溫度、縱向應變水平及預緊力相關的量。此外，推進劑泊松比在千分位上的變化都會對藥柱結構完整性分析帶來重要的影響。然而，在實際發動機結構完整性分析中，泊松比常被處理成常數。由以上分析可知，彈性泊松比的假設勢必會帶來不合理的分析結果。因此，利用粘彈性泊松比替代彈性泊松比進行結構完整性分析是非常有必要的。

一些專家學者對不同彈性泊松比下推進劑藥柱結構時間-溫度相關的力學響應進行了研究，結果表明，當泊松比從不可壓情況下的泊松比ν=0.5變化到可壓情況下ν≠0.5時，泊松比對藥柱結構分析會有特別嚴重的影響[2-3]。盡管以上分析說明了泊松比對藥柱結構分析的影響，但粘彈性泊松比對藥柱結構的影響問題依舊沒有解決。Deng等[4-5]基于Pan等[6]測得的粘彈性泊松比，研究了考慮時間相關泊松比的推進劑本構模型，并采用增量有限元方法對藥柱結構進行了有限元分析，結果顯示，彈性泊松比計算得出的應力應變結果比粘彈性泊松比計算得出的應力應變結果小得多。

本文從粘彈性泊松比的定義出發，通過拉普拉斯變換，建立了考慮粘彈性泊松比的推進劑蠕變型本構模型。針對星孔發動機的點火增壓工況，對粘彈性泊松比的影響進行了研究分析。

1 粘彈性泊松比

在線性粘彈性的情況下，時間相關泊松比可以定義為松弛試驗中，單軸拉伸狀態下橫向變形與初始縱向定應變的比值[7]：

(1)

固體推進劑是典型的熱流變材料，粘彈性泊松比等材料參數符合時溫等效原理，即時間和溫度的不同組合可得到相同的泊松比。這個原理可以表示為

ν(lgt,T)=ν(lgζ,T0)

(2)

其中，縮減時間ζ表示為

ζ=t/αT

(3)

式中αT為時間平移因子。

另一方面，為了描述時間因子的溫度相關性，可利用WLF方程，得到溫度相關的平移因子[8]：

(4)

式中T為當前溫度；Ts為參考溫度；C1和C2為材料參數。

粘彈性泊松比的Prony級數表示為

(5)

當Prony級數項數為5時，函數相關參數見表1。WLF方程在20 ℃下的材料常數C1和C2見表2。

表 1 材料常數Prony級數中的參數

表 2 WLF方程參數

一個完整的本構模型必須有2個以上的獨立材料參數。對于蠕變模型，蠕變模量和泊松比是必不可少的。蠕變模量用Prony級數表示為

(6)

當Prony級數的個數為3時，函數的系數列于表1中。此外，對蠕變模量WLF方程的材料常數列于表2。為了方便計算，定義：

(7)

2 蠕變型本構關系

對于均勻各向同性的粘彈性材料，考慮彈性泊松比，以蠕變模量和泊松比作為參考變量，剪切蠕變模量χ(t)和體積蠕變模量B(t)被定義為

χ(t)=2(1+ν)J(t)

(8)

B(t)=3(1-2ν)J(t)

(9)

但考慮到粘彈性泊松比的影響，式(8)在復域中形式為

(10)

利用逆拉普拉斯變換，式(10)可簡化為

[1+ν(0)]J(t)*dSij+J*(t)*dSij=eij

(11)

其中

(12)

考慮到溫度的影響，式(12)變為

(13)

其中，θ、θ′、ξ和ξ′為縮減時間。

同樣地，對于復數域的蠕變模量：

(14)

粘彈性本構模型中的球形應變如下：

(15)

3 應用分析

為了驗證新提出的蠕變型本構模型以及對粘彈性泊松比的影響特性進行分析，選擇發動機點火增壓工況作為主要研究內容。固體火箭發動機主要由殼體、絕熱層和藥柱等部件組成。為簡化模型和計算方便，采用發動機的軸對稱模型。采用六面體單元，對發動機幾何模型進行網格劃分，有限元模型如圖1所示，該模型包含25 055個六面體單元和31 046節點。在模型的尾部施加軸向的位移約束，在對稱剖面上施加環向位移約束。

圖1 固體火箭發動機的有限元模型

表3列出了發動機中各材料的材料參數。兩個彈性泊松比(粘彈性泊松比的初始值和平衡值)和粘彈性泊松比ν(t)將會被用來進行結構分析。

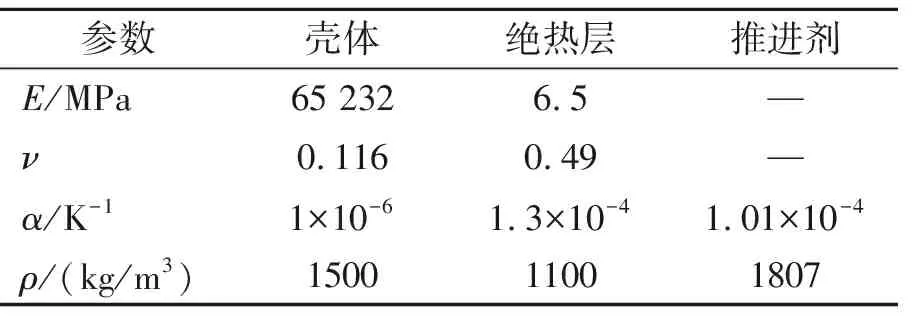
表3 固體火箭發動機的材料參數

發動機的建壓曲線滿足p(t)=p0(1-e-kt),其中p0=6 MPa,k=0.1 s-1。這里分析時間取t=300 s，主要是為了研究響應對時間的依賴性。

推進劑內表面的應變和應力分布是結構完整性的重要分析指標。應變或應力的急劇變化可能會導致非常危險的情況。因此，在發動機內表面選取特征線作為研究發動機內表面的應力應變變化的主要對象，如圖2所示。

圖2 固體火箭發動機內表面特征線示意圖

ν=0.397 7和ν=0.486 4分別代表了粘彈性泊松比的初始值和平衡值。圖3給出了第300 s時發動機內表面特征線上的Von Mises應力應變分布。由圖3可發現，粘彈性泊松比引起的Von Mises應力應變響應介于兩個彈性泊松比引起的Von Mises應力應變響應之間。而由粘彈性泊松比導致的Von Mises應力應變響應明顯高于平衡泊松比引起的應力應變響應。初始泊松比引起的最大Von Mises應力應變分別為1.55 MPa和49.9%，這與粘彈性泊松比引起的最大Von Mises應力1.40 MPa，應變46.0%接近。另外，三種泊松比引起的最大Von Mises應力應變都發生在翼槽位置。從圖3還可發現，由彈性泊松比和粘彈性泊松比導致的Von Mises應力應變在內表面特征線上的分布是一致的。也就是說，粘彈性泊松比并不會導致Von Mises應力應變的突變。此外，從圖3中可明顯看到松弛型(R)和蠕變型本構(C)的計算結果一致，這也說明了本文提出的蠕變型本構的準確性。

(a)Von Mises應力分布

(b)Von Mises應變分布

4 結論

本文從經典粘彈性本構模型出發，利用拉氏變換方法推導出了考慮粘彈性泊松比影響的固體推進劑蠕變型本構模型。該本構模型可考慮不同類型的泊松比(彈性泊松比和粘彈性泊松比)。基于MSC.Marc二次開發技術，將提出的本構模型應用到有限元分析中。針對星孔發動機點火增壓工況，設計了三種泊松比(粘彈性泊松比及其對應的初始泊松比，平衡泊松)，并對這些泊松比的影響進行了分析并得到以下結論：

(1)彈性泊松比與粘彈性泊松比引起的應力應變分布趨勢一致。粘彈性泊松比在發動機結構完整性分析中并不會引起Von Mises應力應變在分布上的突變。

(2)粘彈性泊松比引起的Von Mises應力應變介于初始和平衡泊松比引起的Von Mises應力應變之間，并且與初始泊松比引起的Von Mises應力應變很接近。即對于極短時間內的點火增壓工況，可以利用初始泊松比代替粘彈性泊松比進行結構完整性計算。

(3)仿真結果表明，本文提出的蠕變型本構模型可精確用于發動機結構完整性分析，為后續研究提供指導。