基于粒子群算法的波形自適應設計技術
張羽鑫,刁鳴
哈爾濱工程大學 信息與通信工程學院,黑龍江 哈爾濱 150001
隨著電子技術的不斷發展,信息化戰爭已經逐漸成為了信息時代的基本戰爭形態[1]。在信息化戰爭中,雷達的作戰對象、工作環境和工作任務都發生了極大的變化,傳統雷達在現代化戰爭中所面對的挑戰越來越大,也推動了雷達向著智能化的方向不斷發展。2006年,認知雷達的概念被提出,認知雷達對于環境的適應程度較高,被認為將在現代戰場中扮演極其重要的作用[2]。
在認知雷達的概念被提出之后,國內外的專家便開始了對于認知雷達的研究。目前,對于認知雷達的研究多是聚焦在認知雷達的關鍵技術的研究,其中研究最多的是波形自適應設計技術。目前在波形自適應設計技術研究中常用的5種方法,分別是模糊函數法、特征值法、最大化各類目標之間的距離的方法、動態規劃法、信息論法[3]。以上的方法各有優劣,但是隨著各種智能化算法的提出以及發展,也為我們對于波形自適應設計技術的研究指明了方向[4-5]。
本文針對于信雜比限定下的最大互信息雷達波形設計模型進行研究。該模型作為一種非線性優化模型,通常對于該模型的求解算法采用序列二次規劃算法(SQP算法)。但序列二次規劃算法在對模型的求解過程中,其求解效果會受到尋優起始值的影響,并且在算法的迭代求解過程中,極易陷入局部最優,算法的全局性極差。本文在求解該模型時,在序列二次規劃算法中引入了粒子群算法,將粒子群算法與序列二次規劃算法結合,充分發揮粒子群算法的全局性和序列二次規劃算法局部尋優精確的特性,對模型進行求解,來提升序列二次規劃算法對目標模型的求解效果。
1 信雜比限定下的最大互信息雷達波形設計模型
采用信息論法的自適應波形設計技術中,較為基礎的方法是基于最大互信息準則[6]和最大信雜比準則[7]來進行波形自適應設計。根據雷達檢測理論和信息論的相關知識,分別對于最大互信息準則和最大信雜比準則的求解模型和求解結果進行了研究。
最大互信息準則的波形自適應設計是在雷達發射波形的能量限制下,使得目標和回波之間的互信息最大,即要求解的模型為:
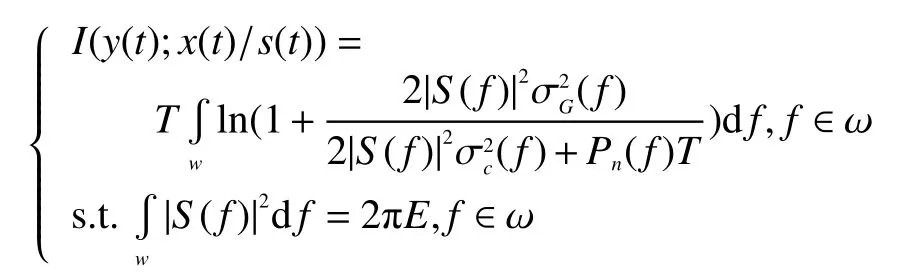
式中: |S(f)|2為預期求解的波形;分別為目標回波、雜波和噪聲的方差;E為限制的發射能量。
利用拉格朗日乘子法對該模型進行求解,得到的雷達發射波形為:
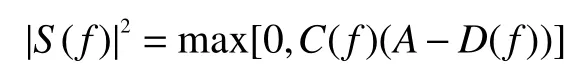
式中:
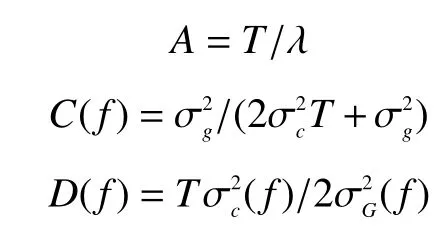
最大信雜比準則則是在雷達發射波形的能量限制下,使得雷達接收到的回波信雜比最大,其目標方程為:
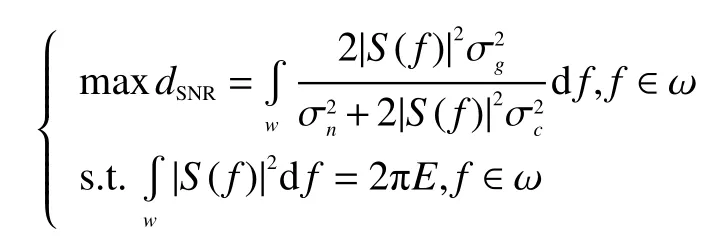
同理,利用拉格朗日乘子法對該模型進行求解,得到的雷達發射波形為:
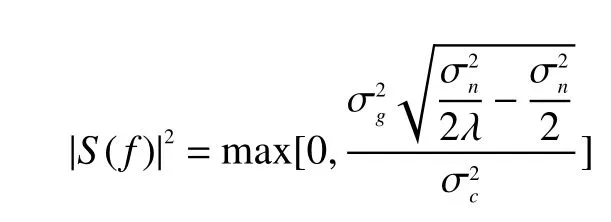
在現實的雷達工作中,雷達為了能夠準確地發現目標,雷達接收系統接收到的雷達回波信雜比需要滿足一定的要求。當接收到的雷達回波的值低于一個門限值,則認為雷達無法探測到該目標,該門限值即為雷達的信雜比限定。將最大互信息準則和最大信雜比準則相聯系,設置信雜比限定為S0,設置本文求解的模型為信雜比限定下的最大互信息雷達波形設計模型為:
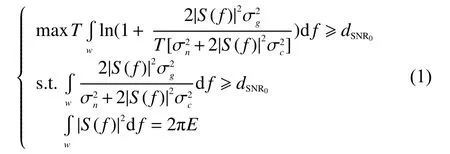
該目標方程式中所要求解的目標函數是目標和回波之間的互信息,雷達的發射能量和接收到的回波信雜比是2個限制條件。本模型即是要在2個限制條件下求解雷達波形,使得目標與回波間的最大互信息量最大。
2 基于序列二次規劃算法的自適應波形優化算法
要求解的信雜比限定下的最大互信息雷達波形設計模型作為一種非線性優化模型,序列二次規劃算法是最為常用的求解該類問題的方法。
序列二次規劃算法的主要思想是:在算法的整個迭代過程中,利用二次規劃子問題來對目標方程的下降方向進行求解,結合價值函數對每一步的求解步長進行求解,并對預期得到的目標矩陣進行更新,求得所要求解問題的最優解[8]。在序列二次規劃算法的整個計算過程之中,核心的步驟就是對預期求解的波形優化模型的下降方向dk進行求解。即將式(1)中的目標函數與限定函數進行求導,形成二次規劃子問題[9]:
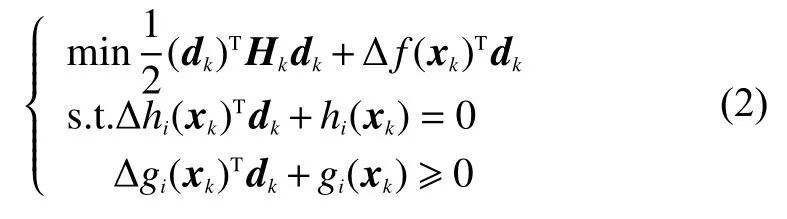
通過式(2)可以對波形優化模型的下降方向dk及拉格朗日乘子進行求解。整體的求解步驟如下:首先將求解得到的dk作為波形優化模型的下降方向;然后利用價值函數來確定每一步迭代的步長,并且利用價值函數和Armijo準則來確定波形優化模型的步長;最后利用迭代公式來確定迭代點。在所有的步驟結束后,利用修正的BFGS公式對Hessian矩陣進行修正[7]。
利用序列二次規劃算法對目標求解的信雜比限定下的最大互信息雷達波形設計模型的計算步驟如下[10]:
1)設置迭代的初始值;
2)將模型轉化為二次規劃子問題,得到求解的模型的下降方向dk;
3)判斷當前點是否滿足以下2個條件:
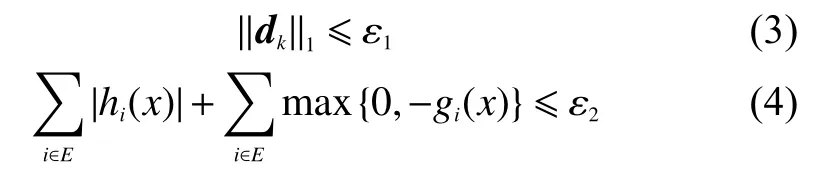
若滿足式(3)、(4)2個條件,則停止仿真,此時的解為求解方程得到的最優解;
4)利用價值函數以及Armijo準則對求解波形優化模型迭代的步長進行計算和確定;
5)利用Armijo準則,對使式(5)成立的最小非負整數進行求解和計算:
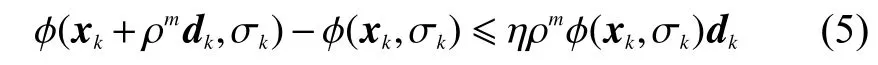
并對波形優化模型的迭代點進行更新:
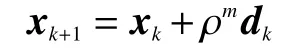
6)利用最小二乘乘子更新算法中的相應參數;
7)用BFGS對Hessian矩陣進行修正;
8)持續迭代,直至迭代停止。
3 粒子群序列二次規劃算法
粒子群算法的計算過程如下[11]:
1)對算法參數進行初始化,包括種群規模的大小、預期解的維數、算法的最大迭代次數;
2)設置解的可行域,在可行域范圍內,對迭代開始時各個粒子的運動范圍和運動速度進行設置;
3)對每個粒子的歷史最優函數值和群體最優位置進行初始化;
4)迭代開始,根據式(6)、(7)更新算法中每個粒子的速度和位置:
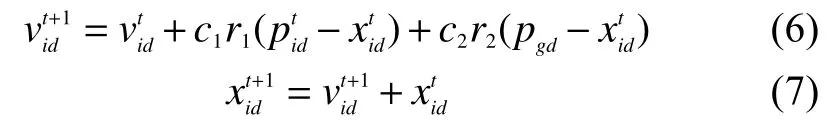
5)持續迭代,實時計算每個粒子的適應度值,針對于本文來講,即求式(1)中的目標函數;
6)根據粒子的函數值更新每個粒子和整個群體的最優位置信息;
7)若當前的迭代次數等于最大迭代次數,則算法結束;否則算法轉向步驟4),繼續進行迭代。
粒子群序列二次規劃算法將序列二次規劃算法作為一個局部尋優的過程,將粒子群算法作為全局尋優的部分,在迭代時,將粒子群算法在計算中粒子得到的全局最優位置作為序列二次規劃算法的初始點,并進行完整的序列二次規劃算法的局部搜索求解。若序列二次規劃算法得到的解優于粒子群算法的全局最優解,則將序列二次算法得到的解直接作為全局最優解進行下一輪迭代;若序列二次規劃的解并不優于粒子群算法的全局最優解,則不對粒子群尋優得到的全局最優解進行修改。該算法將粒子群算法與序列二次規劃算法有機結合起來,發揮了粒子群算法的全局搜索能力和序列二次算法的求解精度能力。算法的工作流程如圖1所示。
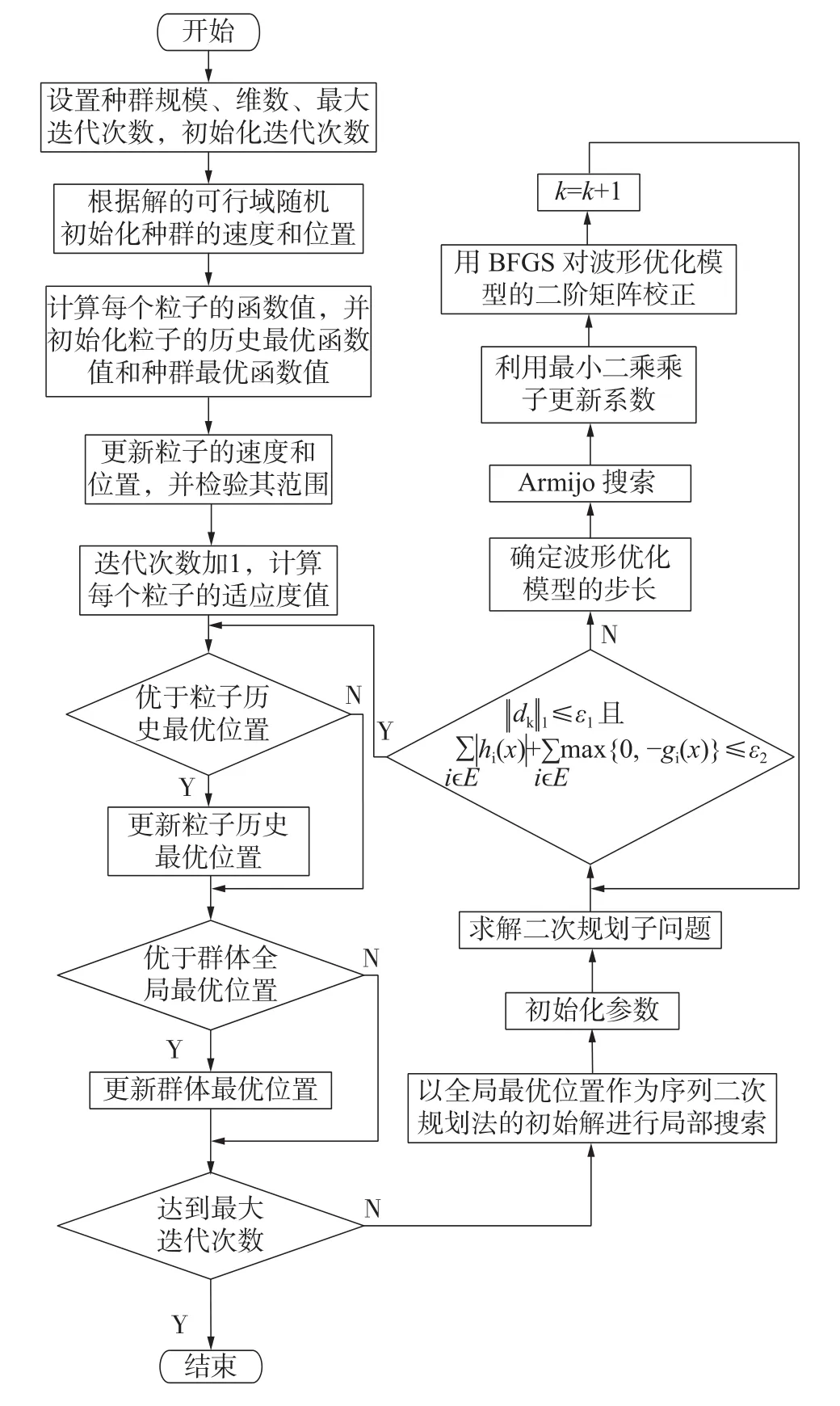
圖1 粒子群序列二次規劃算法流程
4 仿真實驗與實驗結果
為了對算法結果有更加準確的對比,首先使用序列二次規劃算法對目標模型進行求解;在相同的仿真條件下,再使用本文提出的粒子群序列二次規劃算法進行模型求解并比較仿真結果。
4.1 仿真參數設置
仿真時,設置目標與目標間的距離是10 km,雷達的帶寬w是10 MHz,發射載頻fc為1 GHz,雷達工作時,發射波形的頻率范圍為:

設置目標脈沖響應x(t)的譜方差:
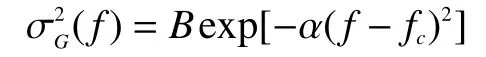
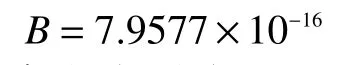
假設噪聲為高斯白噪聲,而且只是熱噪聲,溫度為Ts=300 K,那么:
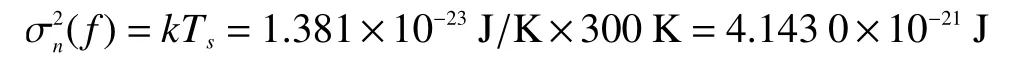
設置最小可檢測信雜比S0為5 dB、發射功率為1 W、序列二次規劃算法最大迭代次數為1 000次、粒子群序列二次規劃算法的最大迭代次數為2 000次,在發射波形長度為T=10 ms時,進行仿真實驗。
傳統的仿真驗證中,目標譜和干擾譜的分布如圖2所示。本文為了便于驗證算法性能,在保證目標譜分布不變時,將干擾譜進行隨機調整,得到如圖3所示的目標譜及干擾譜分布。
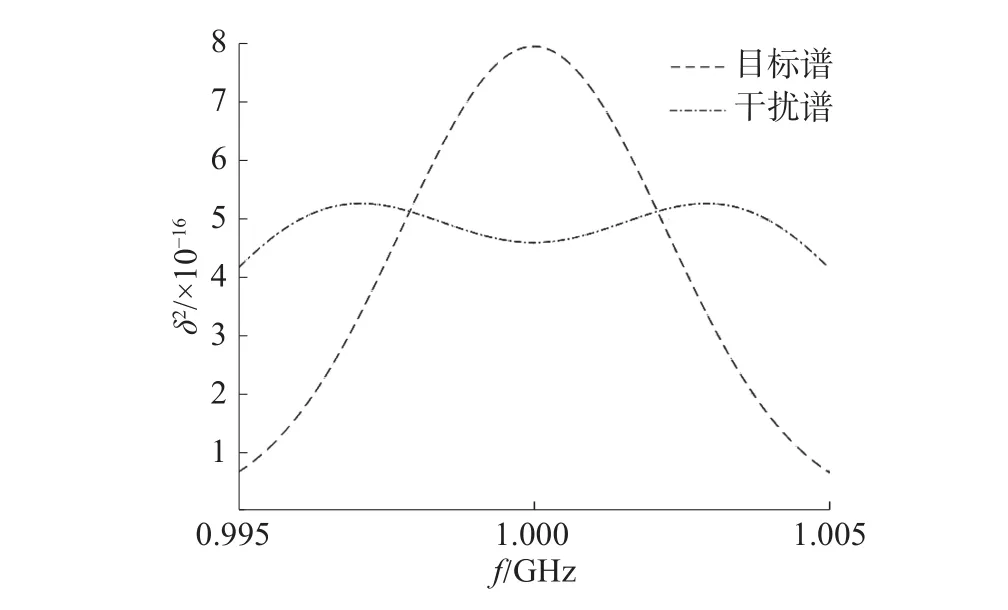
圖2 目標譜和干擾譜分布情況1

圖3 目標譜和干擾譜分布情況2
4.2 序列二次規劃算法仿真結果
采用序列二次規劃算法對模型進行求解,在如圖2所示的干擾譜和目標譜分布情況下,得到在不同的尋優起始點時最優波形的設計結果如圖4所示。
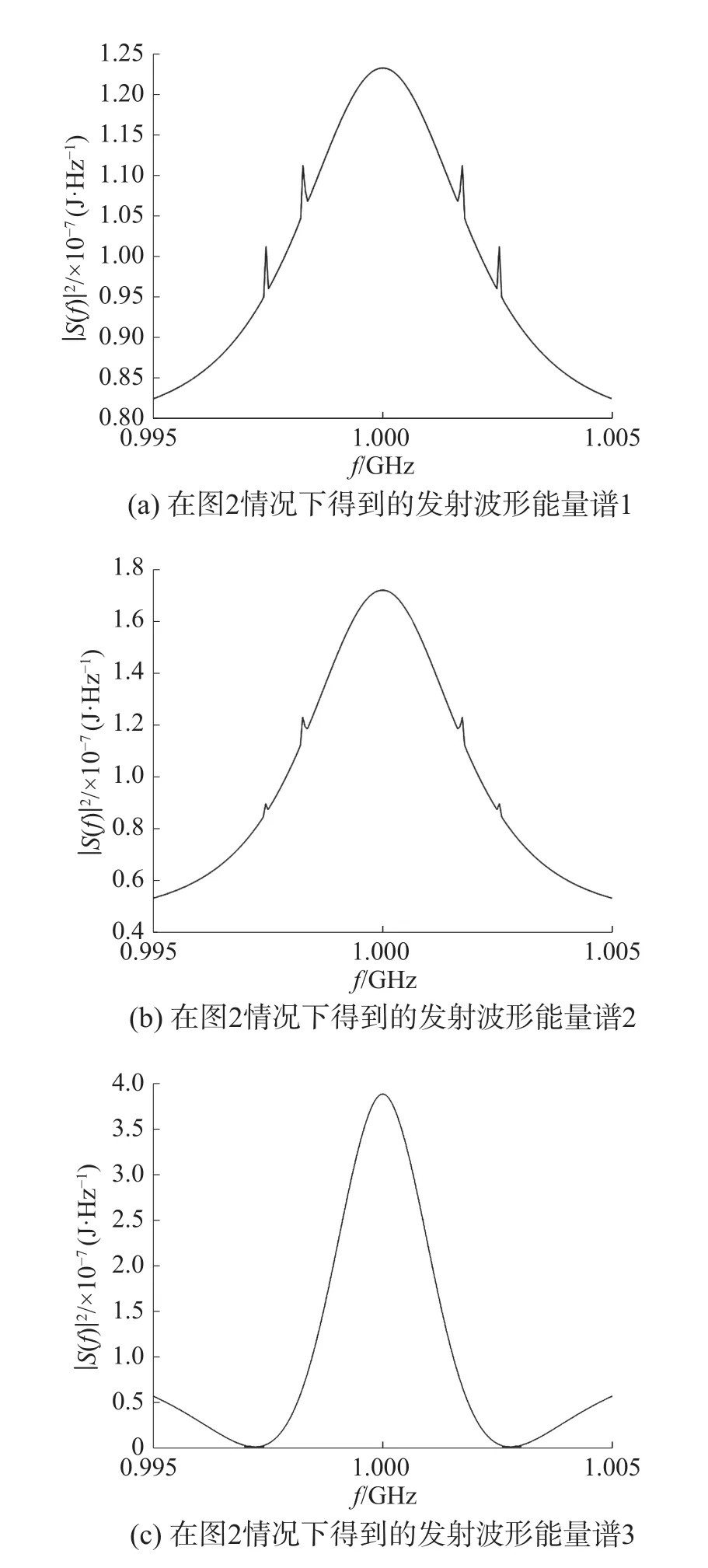
圖4 序列二次規劃算法在圖2情況下求解結果
以上3個仿真過程,迭代次數和每次實驗得到的最大互信息量如表1所示。
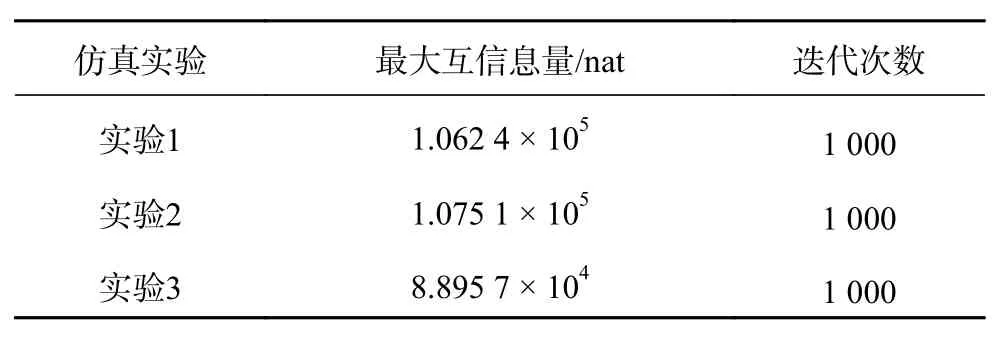
表1 圖4中3個仿真過程最大互信息量及迭代次數
在如圖3所示的干擾譜和目標譜分布情況下,得到的在不同的尋優起始點時得到的最優波形設計結果如圖5所示。以上3個仿真過程,迭代次數和得到的最大互信息量如表2所示。
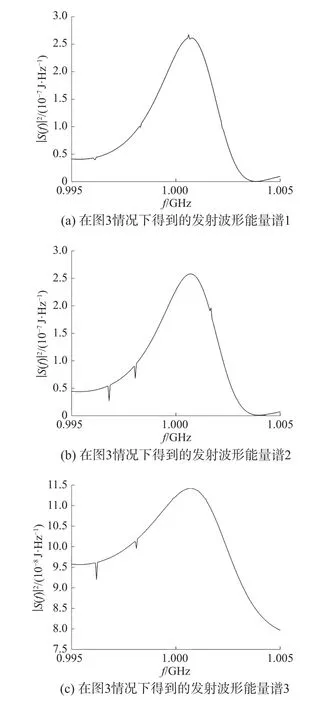
圖5 序列二次規劃算法在圖3情況下求解結果

表2 圖5中3個仿真過程最大互信息量及迭代次數
通過以上結果可以得出,序列二次規劃算法能夠實現對優化模型進行求解。但是在求解過程中,需要人為設置尋優起始點,尋優初始值設定的不同,對算法的結果存在很大的影響。同時算法在運算過程中存在較為明顯的局部收斂現象,算法極易陷入局部最優。
4.3 粒子群序列二次規劃算法仿真結果
在粒子群序列二次規劃算法對于模型的求解過程中,仿真過程所采用的參數與4.2節中一致,采用粒子群的大小為1 000。同樣,在相同的目標譜和干擾譜情況下,分別進行3次實驗,分別記錄這3次實驗得到的最大互信息量和算法收斂時的迭代次數。同時,分別采用粒子群算法和遺傳算法對模型進行求解和算法的對比。使用粒子群序列二次規劃算法對目標模型求解結果的部分仿真圖如圖6、7所示,在不同目標譜和干擾譜分布情況下各個算法對目標模型的求解結果如表3、4所示。
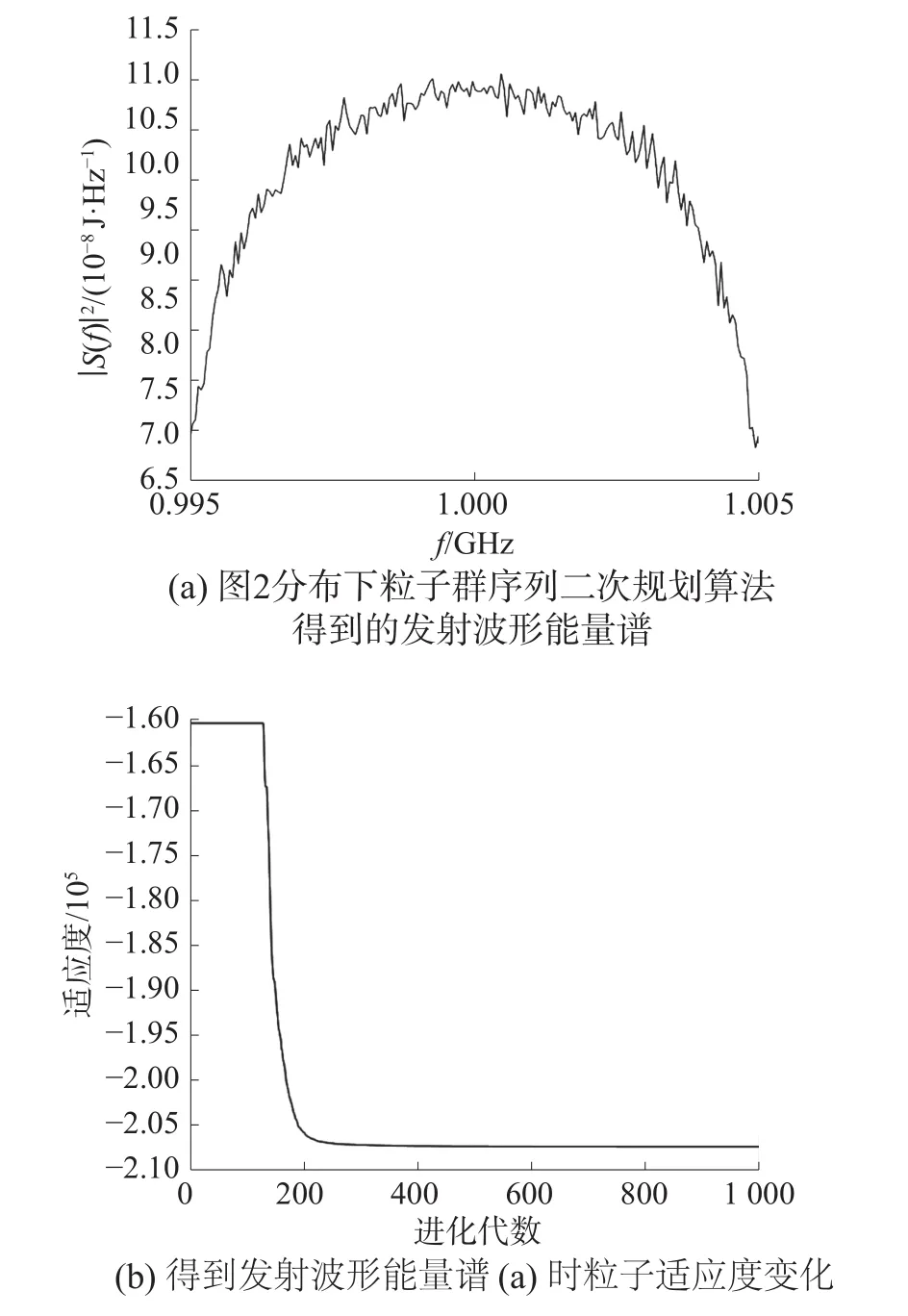
圖6 粒子群序列二次規劃算法在圖2 分布下對目標模型部分求解結果
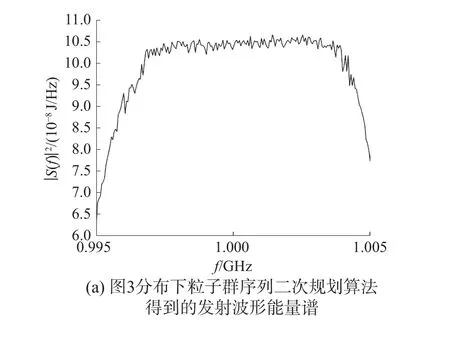

圖7 粒子群序列二次規劃算法在圖3分布下對目標模型部分求解結果
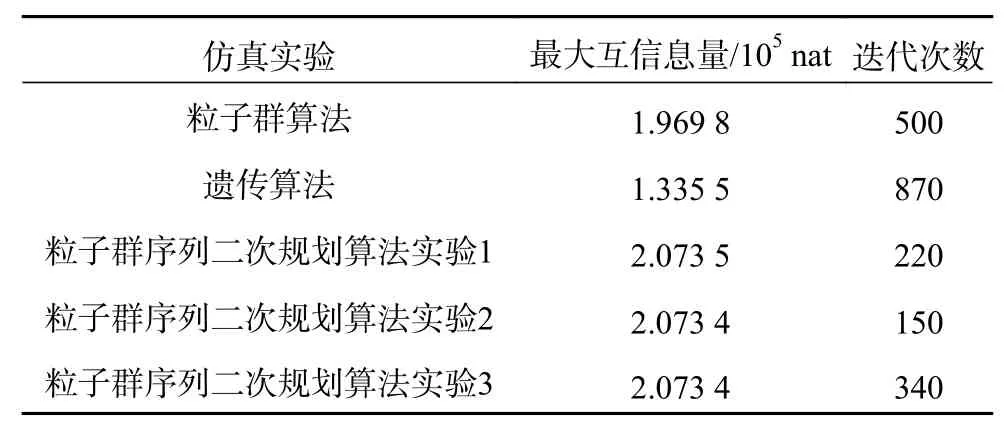
表3 各算法在圖2分布下得到的波形最大互信息量和迭代次數

表4 各算法在圖3分布下得到的波形最大互信息量和迭代次數
通過圖4~7與表1~4中數據可以看出,粒子群序列二次算法在解決信雜比限定下的最大互信息雷達波形設計問題的研究中,有效地提升了傳統序列二次規劃算法、粒子群算法和遺傳算法在解決該問題時的收斂速度和得到的最優波形的最大互信息量,有效地避免了傳統序列二次規劃算法依賴尋優起始點和易陷入局部最優的問題,提高了算法的全局性。
5 結論
本文針對于序列二次規劃算法在計算信雜比限定下的最大互信息雷達波形設計模型中,求解結果易受到尋優初始值的影響、同時易陷入局部最優的問題,在算法中引入了粒子群算法作為全局尋優算法,將序列二次規劃算法作為局部尋優算法,形成了粒子群序列二次規劃算法,并利用該算法對模型進行求解,通過仿真結果可以看出:
1)粒子群序列二次規劃算法因為初始值是隨機設定的,避免了因人為設定尋優初始值導致的計算結果的差別;
2)粒子群序列二次規劃算法在得到最優解時的迭代次數與序列二次規劃算法相比,有明顯的提升;
3)粒子群序列二次規劃算法對模型求解后得到的最優波形的最大互信息量與序列二次規劃算法、粒子群算法、遺傳算法相比,有明顯提升;
4)本文設計的算法,雖然增大了波形設計求解模型的精度,但增大了求解模型所需要的時間消耗,降低了問題處理的實時性。

