求解PageRank 問題的Arnoldi 松弛兩步分裂算法

顧傳青,付友花, 王金波

(1. 上海大學 理學院, 上海200444;2. 保密通信重點實驗室, 成都610041)

PageRank 算法是著名的超鏈分析算法[1], 是當今搜索引擎使用最重要的排序算法之一.PageRank 問題就是求解Google 矩陣首特征值1 所對應的特征向量. Google 矩陣的定義如下:

式中, α ∈(0,1)是阻尼因子, E = veT, e = (1,1,··· ,1)T∈Rn, v = e/n, P是一個列隨機矩陣. PageRank 向量x 是Google 矩陣的主特征向量, 滿足

為解決PageRank 問題, 最經典的算法是易于計算的冪法[1]. 但當阻尼因子α 接近1 時,冪法收斂的速度非常慢. 為了改進算法的收斂速度, Gleich 等[2]利用Richardson 迭代法提出了內外迭代法. Gu 等[3]將冪法和內外迭代法相結合,提出了兩步分裂迭代(power-inner-outer,PIO)算法. 隨后，Xie 等[4]在PIO 算法基礎上提出了松弛兩步分裂(relaxed PIO, RPIO)算法.用于PageRank 問題的Arnoldi 算法[5]是一種重啟的Arnoldi 算法[6]. Wu 等[7]將冪法和重啟的Arnoldi 算法相結合, 提出了深度重啟的Arnoldi 算法. 本工作在文獻[3]的基礎上, 在原有的PIO 算法中加入一個新的松弛參數, 并且運用深度重啟的Arnoldi 算法來加速算法的收斂性, 得到了一個Arnoldi 松弛兩步分裂(Arnoldi-RPIO)算法. 與原有的內外迭代法[2]和PIO 算法[3]相比, 本工作給出的數值算例顯示了新算法的有效性.

1 內外迭代法和深度重啟的Arnoldi 算法

1.1 內外迭代法

根據式(1)和(2), 特征值問題可以轉化為求線性系統

的解, 其中eTx = 1. 考慮到問題在阻尼因子α 越小時越容易求解PageRank, 線性系統(3)可以寫成如下的等價方程:

并通過不動點迭代求解式(4), 即

式(5)可稱為外迭代. 但是, 求解系數矩陣I -βP 的線性系統仍然比較困難. 文獻[2]提出了使用Richardson 迭代法來計算xk+1, 將式(5)中的右端項記為f, 即

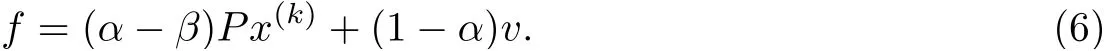
定義內線性系統

然后使用Richardson 內迭代:

外迭代的停止條件為

內迭代的停止條件為

1.2 PIO 算法

在內外迭代法的基礎上, Gu 等[3]提出了PIO 算法來求解PageRank 問題. PIO 算法的迭代格式如下: 給定一個初始向量x(0), 計算

直到向量序列{xk}收斂, 其中0 ＜β ＜α ＜1.

1.3 深度重啟的Arnoldi 算法

考慮如下的特征值問題:

式中, A ∈Cn×n, (λ,x)是矩陣A 的特征對. 給定一個‖v1‖2= 1 的初始向量, 由Arnoldi 過程生成一組Krylov 子空間

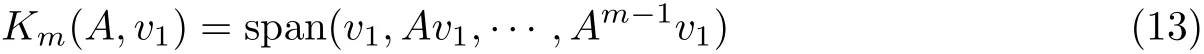
的一組正交基v1,v2,··· ,vm. 在實際求解中,可以用修正的Gram-Schmidt 算法來得到Krylov子空間[8]. 由Arnoldi 過程可以得到

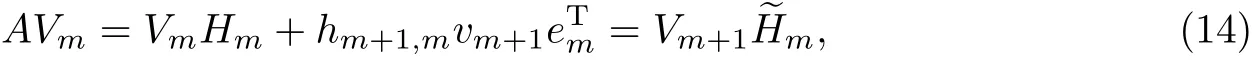
式中, Vm= (v1,v2,··· ,vm)是Krylov 子空間的一組正交基, Hm= {hi,j}m×m∈Cm×m是一個m×m 的上Hessenberg 矩陣, em= (0,0,··· ,0,1)T,Hm∈C(m+1)×m是一個如下的上Hessenberg 矩陣:

深度重啟的Arnoldi 算法的具體步驟如下.

步驟1 給定Krylov 子空間維數m, 所要求的特征對個數p ≤m, 控制精度tol 和單位初始向量v1.

步驟2 運行m 步關于A 和v1的Arnoldi 過程, 得到計算Hm的所有特征對i = 1,2,··· ,m. 將Hm的特征值按模數遞減排序, 從中選出p 個最大的特征對, 轉向步驟6.

步驟3 將vp+1作為初始值運行m-p 步Arnoldi 過程, 得到. 計算Hm的所有特征對(), i = 1,2,··· ,m. 將Hm的特征值按模數遞減排序, 從中選出前p 個特征對.

步驟4 檢驗收斂性. 對于得到的最大的Ritz 值λ1和Ritz 向量y1計算其殘量. 若滿足計算精度, 則選取x1=Vmy1作為PageRank 向量的近似解, 算法停止, 否則繼續.

步驟5 將選出的p 個特征向量yi, i=1,2,···, p, 正交化為2 模單位向量, 得到m×p 矩陣Wp= [w1,w2,··· ,wp]. 如果特征向量yi是復向量, 需要實部和虛部分開存取, 構造m×p階矩陣.

步驟6 通過在Wp的底部增加一行0 形成(m+1)×p 的矩陣Wp= [Wp;0]. 然后令是(m +1) × (m +1) 階單位矩陣Im+1的最后一列. 顯然(m+1)×(p+1)的矩陣Wp+1是正交矩陣.

步驟7 使用舊的Vm+1和Hm形成新的Vm+1和Vm+1Wp+1. 然后令, 返回步驟3.

2 深度重啟的Arnoldi-RPIO 算法

本工作提出利用深度重啟的Arnoldi-RPIO 算法來求解PageRank 問題. 迭代格式如下:

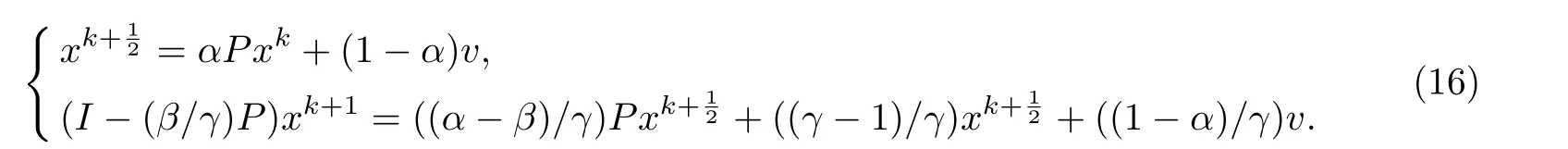
Arnoldi-RPIO 算法在PIO 算法的基礎上引入了一個新的參數γ, 并使用Arnoldi 算法進行深度重啟來加速算法收斂.

Arnoldi-RPIO 算法的具體步驟如下.

步驟1 給定初始化向量v, 選取Krylov 子空間的維數m, 欲保留的特征向量數p, 外迭代的收斂精度τ, 內迭代的收斂精度η, 參數α, β, 控制內外迭代與Arnoldi 算法階段的轉換參數α1和α2, maxit, restart=0, 外迭代的誤差r =1, 內迭代的誤差d=1,d0=d.

步驟2 運行1.3 節算法2～3 次. 若是第1 次運行, 則運行步驟2～7, 否則運行步驟3～7.如果殘差范數滿足收斂精度, 則算法停止, 否則繼續.

步驟3 將由深度重啟的Arnoldi 算法得到的PageRank 向量的近似解x1作為內外迭代法的初始向量.

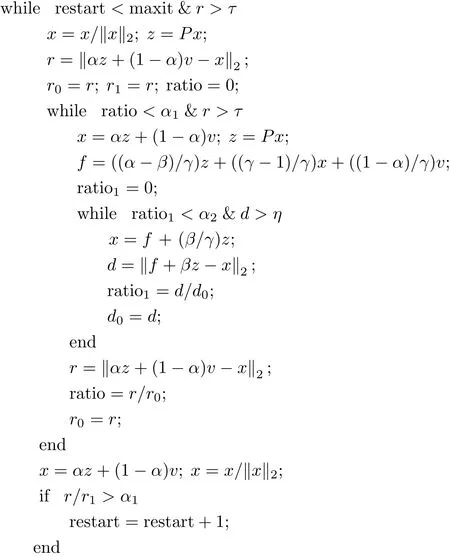
end if r ＜τ, 算法停止, 否則轉向步驟2.

關于Arnoldi-RPIO 算法有如下幾點說明: ①參數α1, α2, restart, maxit 是用來控制內外迭代法和深度重啟的Arnoldi 算法的轉換; ②定義rcurr為一次內迭代后的殘差范數, rpre為一次內迭代前的殘差范數, ratio = rcurr/rpre為內迭代前后相鄰殘差范數比; 同時定義ratio1為內迭代中當前步的殘差范數和上一步的殘差范數之比(這里給出ratio 和ratio1的定義是為了保證算法的運算效率); ③通過比較每一次進入內外迭代前后的殘差范數比ratio = rcurr/rpre與α1的大小, 來決定是否執行restart=restart+1; 通過maxit 控制restart 的次數, 如果restart＞maxit, 則中止內外迭代法階段, 進入深度重啟的Arnoldi 算法階段, 否則繼續運行內外迭代法.

在實際求解中, α1和α2的選擇非常關鍵. 由于ratio1=d/d0, ratio=r/r0, 所以這兩個參數很自然地小于α (冪法的收斂速率是α). 本工作中選擇α1=α-0.1, α2=α-0.1. 事實上,如果令γ =1, 則Arnoldi-RPIO 算法就等價于文獻[7]提出的Arnoldi 算法.

3 Arnoldi-RPIO 算法的收斂性分析

RPIO 算法和深度重啟的Arnoldi 算法的收斂性分別在文獻[4, 9-10]中被證明. 不妨假設A 是一個對角化矩陣, 并且x1和子空間Km的距離定義為

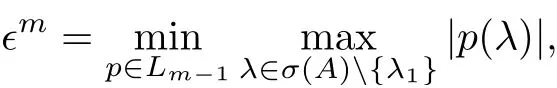
式中, Lm-1表示次數小于m-1 的多項式集, 并且p(λ1)=1, σ(A)表示A 的特征值集. 不失一般性, 假設A 的特征值降序排列:

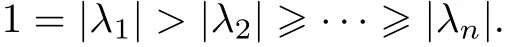
引理1[9]假設A 是一個對角化矩陣, Arnoldi 算法的初始向量v1可以展開為v1=是特征基, 且‖xi‖2= 1, i = 1,2,··· ,n,, γi/= 0, 則如下的不等式成立:

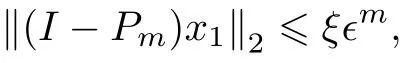
式中, Pm是子空間Km(A,v1)上的正交投影,

將由深度重啟的Arnoldi 算法得到的v1作為RPIO 算法的初始向量. RPIO 算法得到向量v*1=ωGkv1, 其中k ≥maxit,

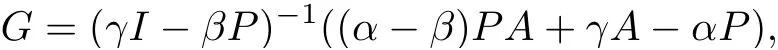
ω 是正規化因子. 在Arnoldi-RPIO 算法的下一步循環中, v*1將被作為Arnoldi 過程的初始向量, 這樣就可以得到一個新的Krylov 子空間:

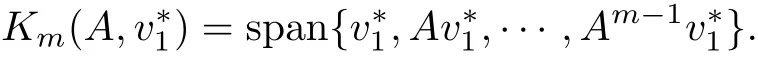
下面的定理證明了本工作給出的新算法的收斂性.

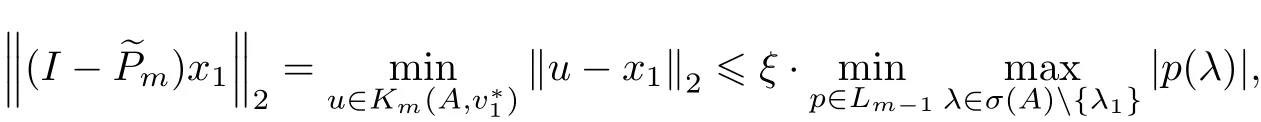
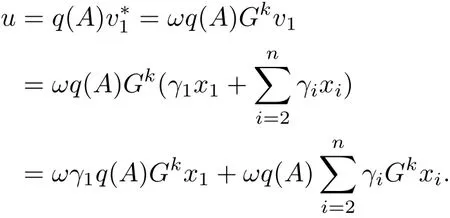
因為

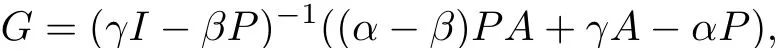
可以推出

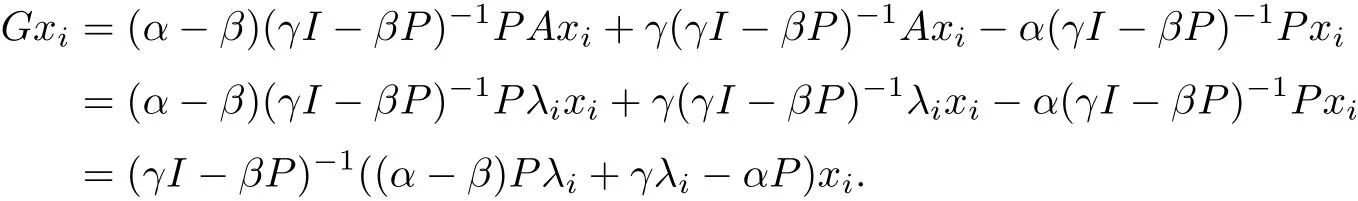
假設πi是P 的一個特征值,可知是(I -βP)-1的一個特征值. 由

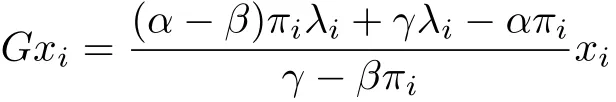
和λ1=1, 得到Gx1=x1,Gkx1=x1. 再令

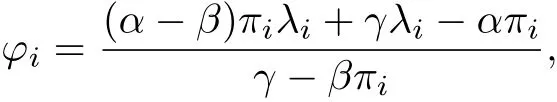
對于i=2,3,··· ,n, 由于|λi|≤α, γ ≥1, 可以推出

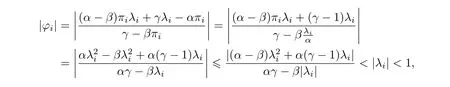
從而得到如下兩個關系式:

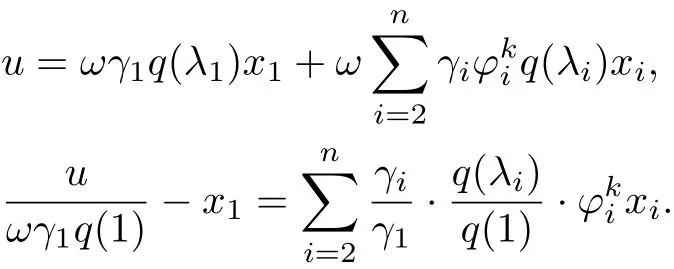
現在令p(λ)=q(λ)/q(1), 則p(1)=1, 從而得到

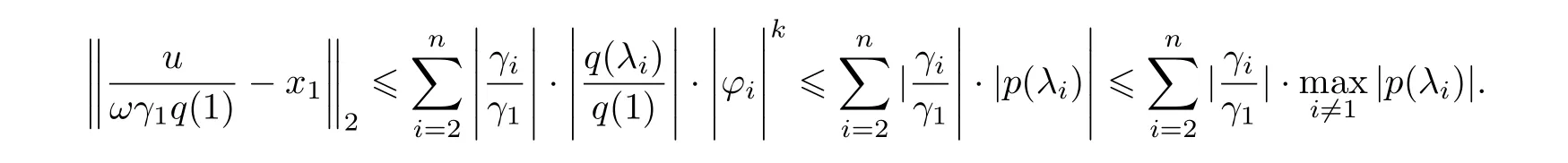
因此, 證明了

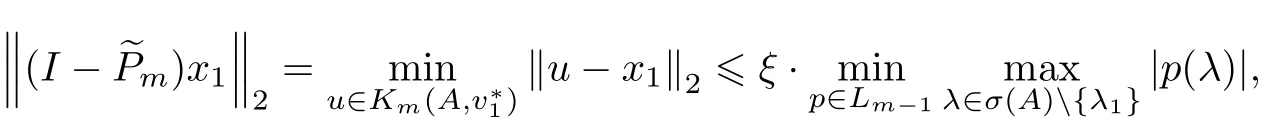
4 數值算例

本工作選擇Stanford-Berkeley 矩陣作為測試矩陣, 給出數值算例來展示Arnoldi-RPIO算法的有效性, 并將其與內外迭代法和PIO 算法進行對比. 數值算例是在內存為4 GB, 處理器為2.53 GHz Intel(R)Core(TM)i3 M CPU 的電腦上用MATLAB(R2014a)程序進行的. 這里, Mat-Vec 表示矩陣向量乘積的次數, CPU 表示運算時間, 單位為s.

為保證實驗的公平性, 阻尼因子α 的取值分別為0.990, 0.993, 0,995, 0.998, β =0.5, 內外終止條件均為η =10-2, τ =10-8. 在Arnoldi-RPIO 算法中, 參數α1=α-0.1, α2=α-0.1.為了描述Arnoldi-RPIO 算法的有效性, 定義

表1 列出了測試矩陣的特征, 包括矩陣的維數(n)、非零元個數(nn)和稠密度(den), 并定義表2 和圖1 列出了3 種算法的數值結果.

表1 測試矩陣的特征Table 1 Characteristics of test matrix

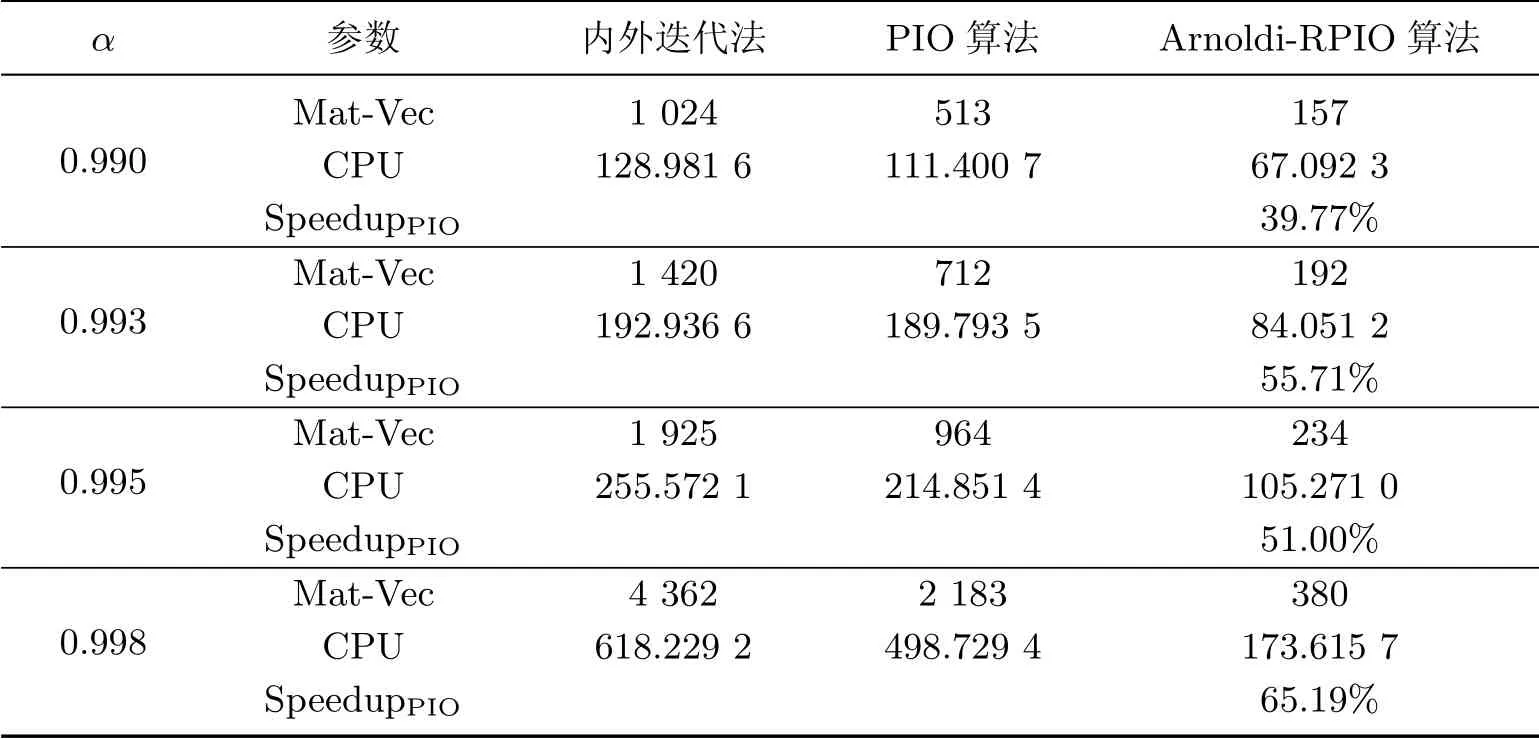
表2 關于Stanford-Berkeley 矩陣3 種算法的數值結果Table 2 Numerical results of three algorithms for Stanford-Berkeley matrix

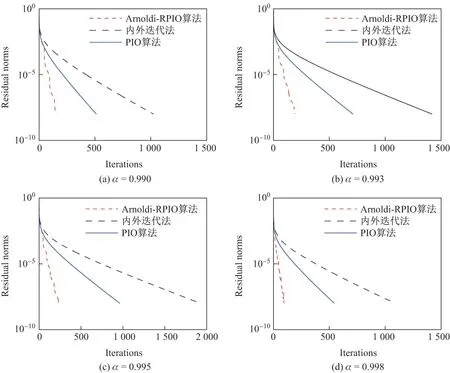
圖1 關于Stanford-Berkeley 矩陣3 種算法的收斂性分析, τ =10-8Fig.1 Convergence analysis of three algorithms for Standford-Berkeley matrices, τ =10-8

圖1 描述了阻尼因子α 取不同值時3 種算法的收斂軌跡. 算例中Arnoldi-RPIO 算法選取的參數為γ = 6,m = 8,p = 4, maxit=40. 觀察表2 的數值結果發現, Arnoldi-RPIO 算法在Mat-Vec 和CPU 兩個方面的表現都是最好的. 對于Stanford-Berkeley 矩陣, 數值結果顯示: 當α = 0.998 時, Arnoldi-RPIO 算法耗時250.101 4 s 達到的收斂精度, PIO 算法需耗時575.583 5 s 才能達到; 并且阻尼因子α 取值越接近于1 時, 本工作給出的Arnoldi-RPIO 算法的計算效果就越好.