非對稱的Lp-徑向差體

齊繼兵

(1. 上海大學理學院, 上海200444; 2. 合肥師范學院數學與統計學院, 合肥230601)

1 已有結果

近幾年, 非對稱的Lp-Brunn-Minkowski 理論是凸幾何理論的一個新的而且發展迅速的方向[1-16]. 本工作給出了文獻[14]的對偶結果, 研究了關于星體的非對稱Lp-徑向差體的一些性質, 建立了關于非對稱的Lp-徑向差體的均值積分的幾何不等式. 作為其特例, 得到非對稱Lp-徑向差體體積的一些不等式.

設φn為n 維歐氏空間Rn中全體星體(關于原點)的集合, 關于原點對稱的星體的全體記為φns. 設K ∈φn, 其徑向函數定義[17]為

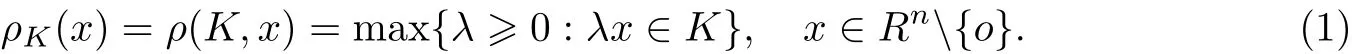
對于兩個星體K,L, 如果存在一常數λ ＞0, 使得它們的徑向函數滿足ρ(K,·) = λρ(L,·),則稱這兩個星體相互膨脹. 設K,L ∈φn,p ≥1,λ,μ≥0 不全為0, Lp-徑向線性組合λ·L ∈φn定義[17]為

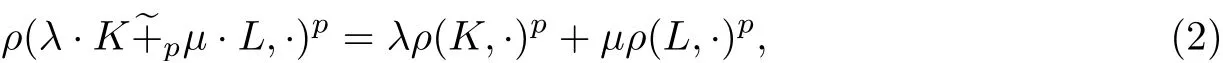
式中, λ·K =λp1K. 特別地, 當p=n-1 時, λ··L ∈φn稱為徑向Blaschke 線性組合[18]; 當p ≤-1 時, λ·μ·L ∈φn稱為調和-p 組合[19].

設K ∈φn,p ≥1,τ ∈[-1,1], 引出Lp- 徑向差體K 與非對稱的Lp-徑向差體定義為

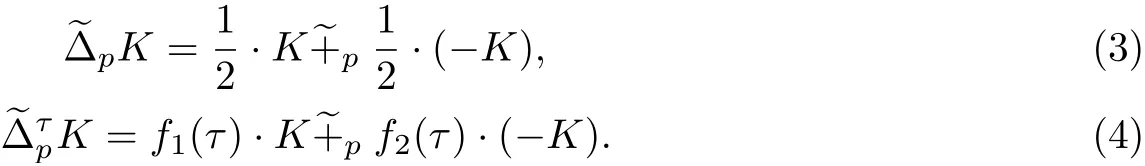
這里

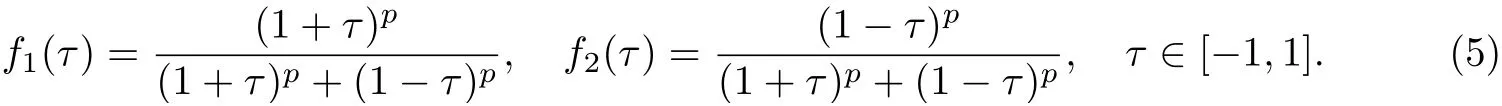
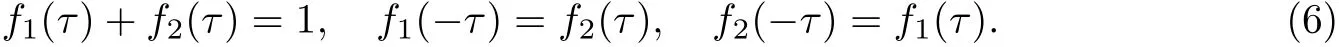
設K ∈φn, K 的第i 個對偶均值積分定義[17]為

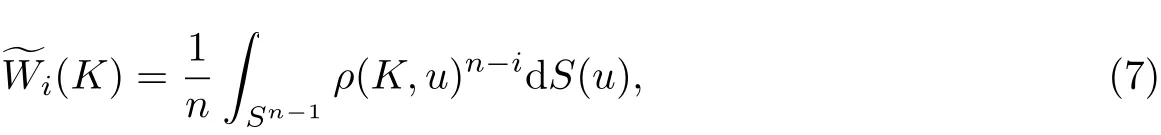
式中, S(·)為通常的球面Lebesgue 測度.

在φn中, 星體K的一種對偶被稱為星對偶, 定義[20]為

本工作的主要目標是研究關于星體的非對稱徑向差體及其星對偶的對偶均值積分的極值問題. 進一步地, 本工作給出了關于星體的對偶Blaschke-Santal′o 型不等式.

定理1 設K ∈φn,τ ∈[-1,1], p ≥1,0 ≤i ≤n-1, 則有

如果K 不關于原點中心對稱, 則左邊不等式等號成立當且僅當τ =0; 右邊不等式等號成立當且僅當τ =±1. 如果K 關于原點中心對稱, 則式(9)中的兩個不等式是恒等式.

推論1 設K ∈φn, τ ∈[-1,1], p ≥1, 則有

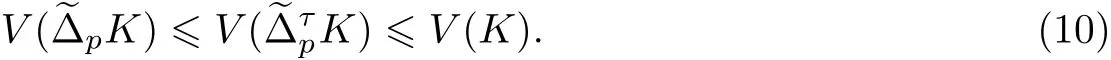
如果K 不關于原點中心對稱, 則左邊不等式等號成立當且僅當τ =0; 右邊不等式等號成立當且僅當τ =±1. 如果K 關于原點中心對稱, 則式(10)中的兩個不等式是恒等式.

定理2 設K ∈φn,τ ∈[-1,1], p ≥1,0 ≤i ≤n-1, 則有如果K 不關于原點中心對稱, 則左邊不等式等號成立當且僅當τ =0; 右邊不等式等號成立當且僅當τ =±1. 如果K 關于原點中心對稱, 則式(11)中的兩個不等式是恒等式.

在定理2 中取i=0, 可得到如下推論.

推論2 設K ∈φn, τ ∈[-1,1], p ≥1, 則有

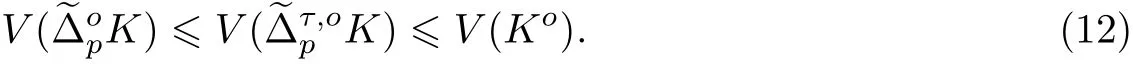
如果K 不關于原點中心對稱, 則左邊不等式等號成立當且僅當τ =0; 右邊不等式等號成立當且僅當τ =±1. 如果K 關于原點中心對稱, 則式(12)中的兩個不等式是恒等式.

設ωn為歐氏空間Rn中單位球的體積, 則可獲得如下關于星體的非對稱Lp徑向差體的對偶均值積分的對偶Blaschke-Santal′o 型不等式.

定理3 設K ∈φn,τ ∈[-1,1], p ≥1,0 ≤i ≤n-1, 則有

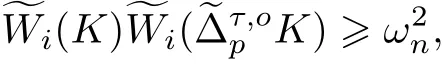
等號成立當且僅當K 為球心在原點的球.

推論3 設K ∈φn,τ ∈[-1,1], p ≥1, 則有

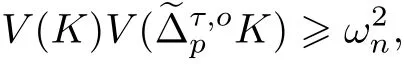
等號成立當且僅當K 為球心在原點的球.

2 準備工作

設K,L ∈φn,p ≥1,λ ≥0,μ≥0(不全為0), 調和p-組合λ··L定義[17,19]為

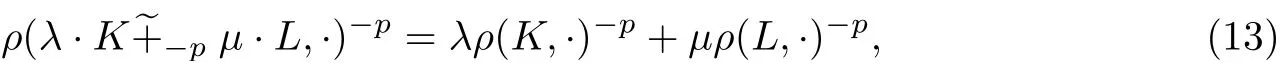
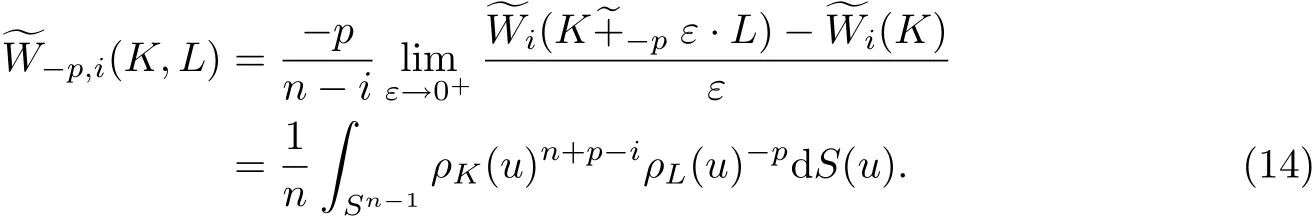
設Q,K,L ∈φn,p ≥1,λ ≥0,μ≥0(不全為0), 結合式(13)和(14), 有

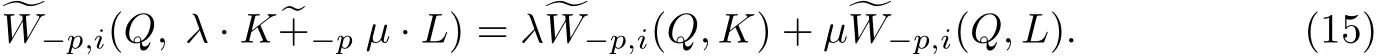
引理1[21]如果K,L ∈φn,p ≥1,λ,μ＞0, 0 ≤i ＜n, 那么

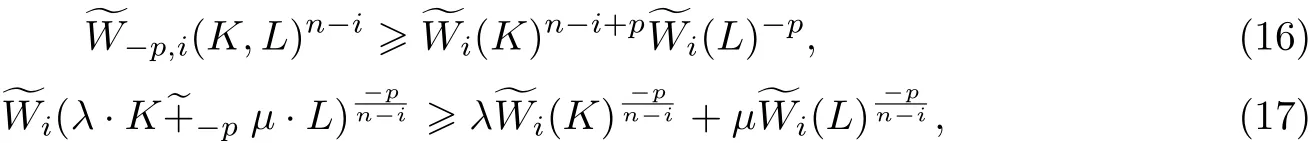
式(16)和(17)等號成立當且僅當K 和L 互為膨脹.

引理2[22]若K,L ∈φn,p ≥1,λ,μ＞0, 0 ≤i ≤n-1, 則等號成立當且僅當K 和L 互為膨脹.

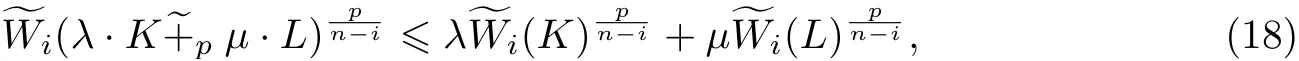
根據Cauchy-Schwartz 不等式以及式(7)和(8)容易得到下面的引理.

引理3 設K ∈φn,0 ≤i ＜n, 則

等號成立當且僅當K 是中心在原點的球.

3 非對稱Lp-徑向差體的一些性質

為了證明主要結果, 本工作給出了關于非對稱Lp-徑向差體的一些性質.

定理4 設K ∈φn, τ ∈[-1,1],p ≥1,φ 為非退化的線性變換, 有

若τ /=0, 則

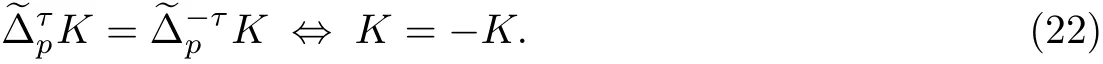
證明 設u ∈Sn-1, 由式(1), (2)和(4), 可得

式(20)得證. 根據式(5), (8)和(9), 有

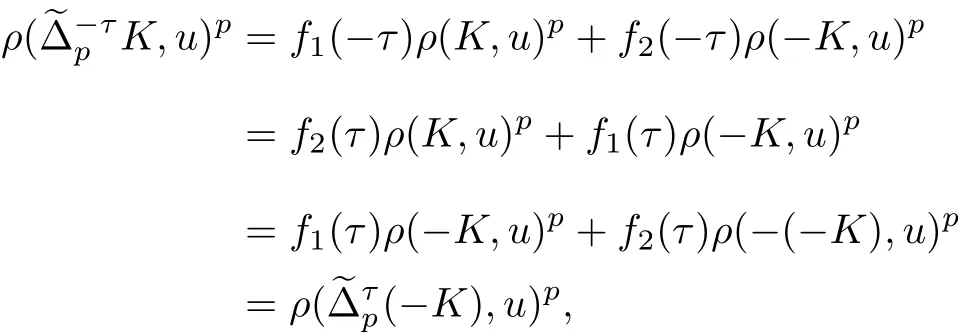
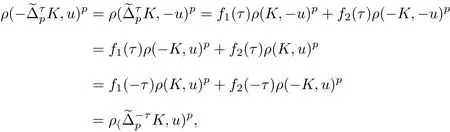
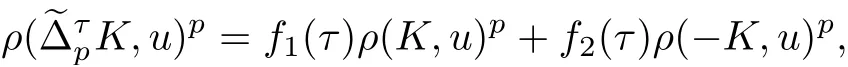
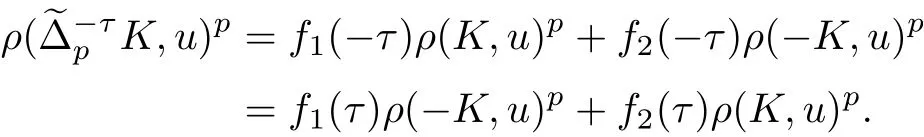
根據定理4, 容易得到下面3 個推論.

推論4 設τ ∈[-1,1], p ≥1,K ∈φn, 但

推論5 設K ∈φns,τ ∈[-1,1], p ≥1, 則

推論6 設K,L ∈φns,τ ∈[-1,1], p ≥1, 則

4 主要結果的證明

4.1 定理1 的證明

設K ∈φn, τ ∈[-1,1],p ≥1,0 ≤i ≤n-1. 根據式(4)和(18), 可得

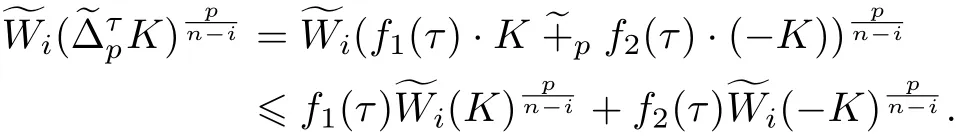
根據式(2)和(4), 對于任意的u ∈Sn-1, 有

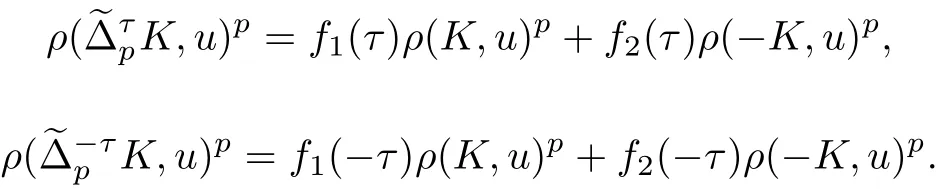
由式(6), 有

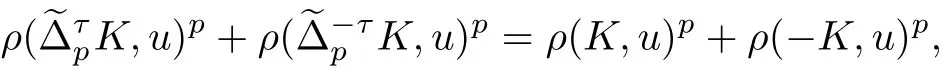
即

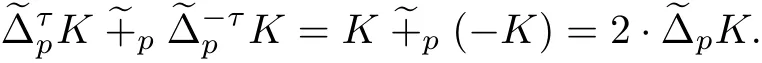
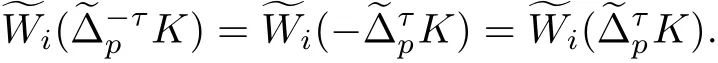
所以

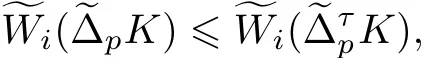
4.2 定理2 的證明

設K ∈φn, u ∈Sn-1, 由式(1)和(11), 有

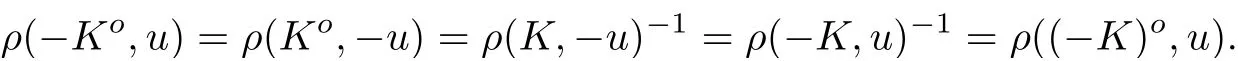
因此

對于τ ∈[-1,1], p ≥1, 由式(4), (8), (13)和(23), 得到

所以

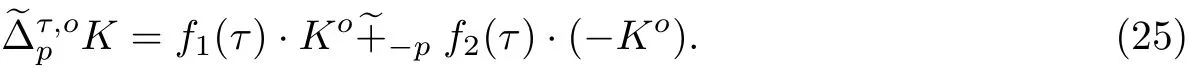
對于0 ≤i ≤n-1, 結合式(17)和(25), 得到

等號成立當且僅當f1(τ)f2(τ)=0 或Ko和-Ko互為膨脹. 如果f1(τ)f2(τ)=0,則τ =±1.如果Ko和-Ko互為膨脹, 有Ko=-Ko, 根據式(8)和(23), 也就是說K =-K. 再根據推論5, 若K = -K, 則對于任意的因此不等式組(11)右邊的不等式得證.

根據式(7), 得到

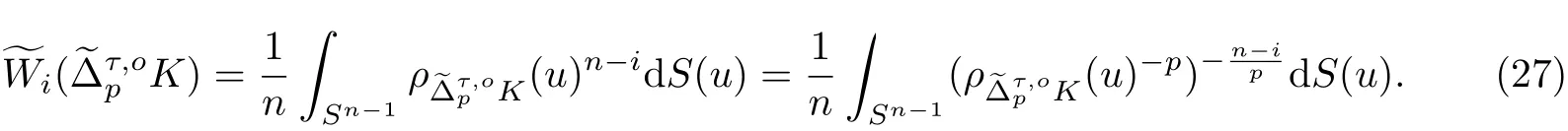
對于τ ∈[-1,1], 利用文獻[4, 14]的證明技巧, 計算函數關于τ 的導數.根據式(14), (24) 和(27), 有

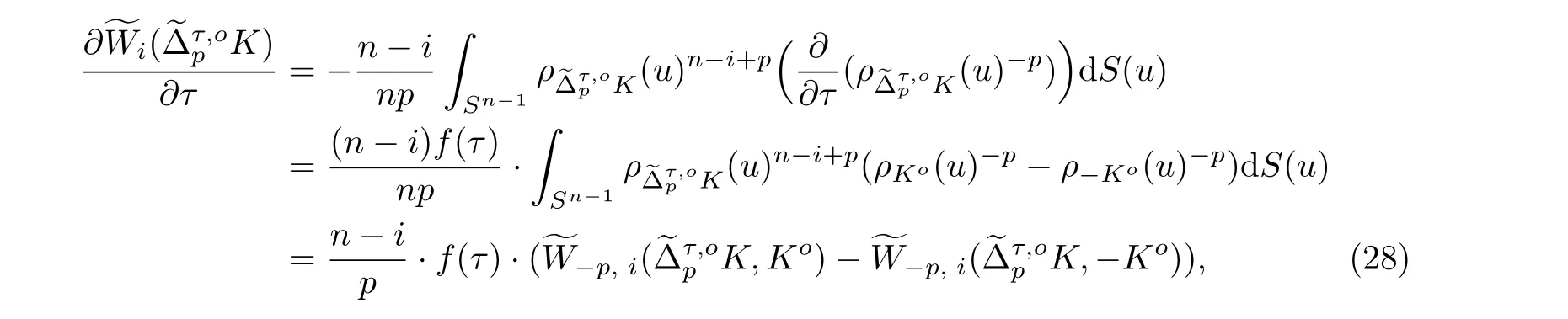
這里

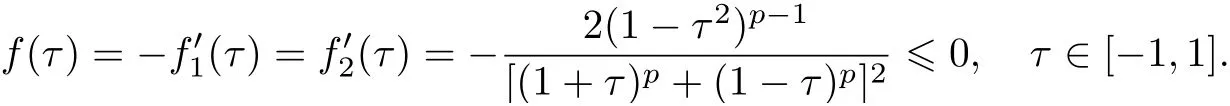
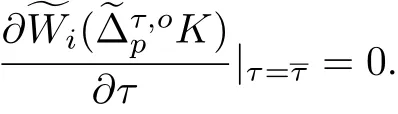
由式(28), 等價于

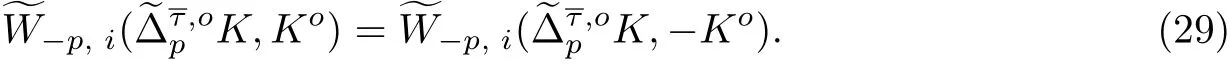
根據式(23)和(25), 有

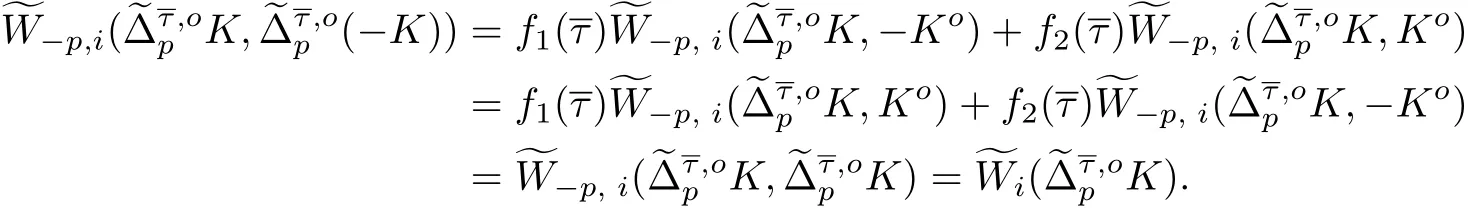
根據式(16), 得到

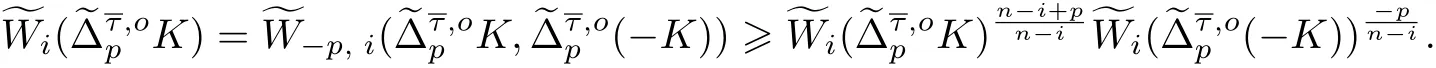
因為p ≥1,0 ≤i ≤n-1, 所以

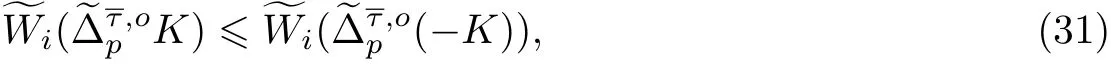
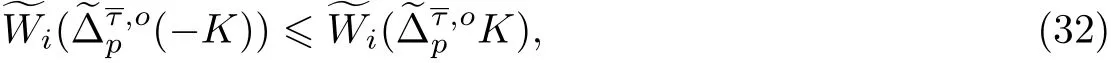
結合式(31)和(32), 得到

根據式(13), (30)和(33), 對于任意的u ∈Sn-1, 有

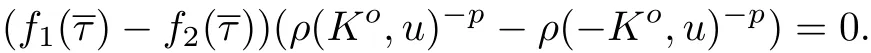
如果ρ(Ko,u)-p= ρ(-Ko,u)-p對于任意的u ∈Sn-1成立, 根據式(8)和(23), 這等價于K =-K. 再根據推論5, 如果K =-K, 得到

因此式(11)左邊的不等式得證.

根據式(11), (26)和(34)可知, 如果K 不關于原點中心對稱, 則式(11) 左邊的不等式等號成立當且僅當τ = 0, 右邊的不等式等號成立當且僅當τ = ±1. 如果K ∈φns，即K 關于原點中心對稱, 則式(11)中左右兩個不等式是恒等式. 綜上，定理2 得證.

4.3 定理3 的證明

設K ∈φn, τ ∈[-1,1],p ≥1,0 ≤i ≤n-1, 根據式(9), (11)和(19), 有

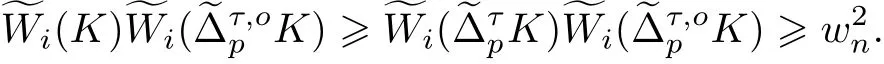
由式(9)和(19)的等號成立條件, 得到式(12)中等號成立當且僅當K 為中心在原點的球.