基于MB+樹的數據庫查詢算法優化

范會芳

摘要：當今社會人們工作、生活中大數據被廣泛應用。在運行數據庫過程中，操作頻率最高的是查詢操作。對基于MB+樹的數據庫查詢算法進行優化，通過構建MB+樹型、MB+查詢算法以及插入算法，實現數據查詢算法的優化構建。為驗證優化后算法的最優性，分別以傳統的基于R樹的數據庫查詢算法、Merkle散列樹查詢算法為對照組，驗證MB+樹算法的查詢效率和查詢消耗。結果表明：優化后的MB+樹數據庫查詢算法，查詢效率明顯優于傳統算法，查詢消耗少于傳統算法。

關鍵詞：MB+樹;數據庫;查詢算法;優化

中圖分類號：TP312? ? ? 文獻標識碼：A

文章編號：1009-3044（2019）19-0011-03

MB樹是一種基于貝葉斯網絡的、結合Merkle的散列概念[1-2]。數據庫系統查詢結構適合采用B+樹，結構寬而淺的樹型，其對大型數據庫的索引具有出色表現。是一種適用于組織動態的、平衡的多分樹索引結構。常規的數據庫管理系統之中，廣泛應用B樹及其變形。MB+樹在每一個節點結構中增加散列值項，以貝葉斯網絡作為概率圖模型解決存儲和查詢問題，合并當前節點的所有子節點散列值，進行儲存，以便于為后續的查詢和檢驗提供輔助信息。MB+樹也是一種特殊的R樹，具有R樹基特性，為減少I/O代價，需要在訪問中間節點時，根據MB+樹的序關系，進行大量的剪枝，簡化查詢算法步驟，減少訪問節點數。

1 基于MB+樹的數據庫查詢算法優化

1.1 構建MB+樹樹型

本文采用與構造常規樹型數據結構相同的方式，來構建MB+樹。在建構一個值為null的MB+樹樹根節點的基礎上，將數據文件塊的檢索鍵和指針逐一向對應的null節點結構中加入。進行分裂操作，調整各個節點的數據項數，要符合當前節點中數據項小于等于節點階的要求，以此確保新MB+樹有效[3]。

MB+樹的查找效率明顯和查找樹中任意記錄所需的平均節點數有關系。假定MB+樹的節點中已包含n個檢索鍵。新的檢索鍵和指針項加入后，會使節點內的數據項數目增加，節點內的數據項數將大于n，需要對節點進行分裂，保持構建MB+樹的有效性。

1.2 MB+樹節點插入

節點插入算法從根節點逐層向下搜索應插入的節點位置，到找到葉子節點位置為止。利用MB+樹中間節點幾何位置的有序性，在每層搜索中，可快速定位應出入的節點[4]。查詢算法程序的數據插入，第一步查詢此數據是否在MB+樹中，若數據存在，找到其在MB+樹中的對應位置，將數據插入;若數據不存在，就會有可能導致節點分裂。應先找到數據點位置，插入算法之前，查看該位置是否空。如果數據點位置為空，可調整指針，直接插入數據點。為了在插入數據后，仍具有 MB+樹的特征，重新生成子樹。調整會改變MB+樹的有序性，為保證MB+樹自身有序性不變化，記錄調整結束時節點層數。調整結束后排序方式發生改變，需要按照記錄的層數的排序方式，重新生成子樹，使得最后得到的整個樹都具有MB+樹的特性。

存儲數據項和索引項時還要知道該節點是否滿。已滿的數據節點無法進行運算及存儲，不能用節點中索引項數量衡量已占用空間[5]。因此，在本文優化的算法中，采用 [Pd]- [Pi]來表示節點中剩余空間。根據（1）、（2）對數據庫內數據進行優化查詢。

[Y′=Y-Y/T]? ? ? ? ? ? ? ? ? ? ? ? ? （1）

[T=jPYj-Y2p-1]? ? ? ? ? ? ? ? ? ? ? ?（2）

其中，p為數據項和索引項的總和，T為設定查找周期，Y為數據庫內部數據。

如果查找出的數據不是所需要的，要根據記錄搜索順序文件的搜索碼鏈表。快速定位記錄位置，保證較高的存儲效率，減少節點的插入和刪除的開銷維護。

1.3 MB+樹查詢流程優化

基于MB+樹的數據庫數據查詢，應快速檢索并得到數據文件塊的基本信息的能力。本文采用的MB+樹是基于Merkle散列樹，發展起來的數據查詢流程。根據二路分支的原則，沿二叉樹的左右分支向下進行遍歷查找。執行查詢操作，如果需要隨機查找，找到所要求的記錄需要通過索引樹。從root節點起始找起，通過順序集找到記錄。通過索引樹或從順序集的鏈頭得到的，某一順序節點開始找起。中間節點中的指針，根據節點結構，指向下一層的某一塊數據。除了指向具體記錄，這一層最右側指針還指向下一個葉子節點。由當前節點的出度決定，根據MB+樹的定義，基于MB+樹的數據查詢流程，需進行遍歷查找，按照z路分支原則，完成查詢流程 [6]。引入枝葉比[Rbl]的概念，用來描述葉子節點和非葉子節點的數量關系。

[Rbl=RbRl]? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?（3）

[Rb]為非葉子節點最大關鍵字數目，[Rl]為葉子節點最大關鍵字數目。

假定需要查找檢索鍵為K的數據文件塊，z路分支的遍歷查找過程由以下三個步驟組成：

第一步，判斷ROOT中包含的各個檢索鍵與待索檢的K之間的大小關系。從MB+樹的根節點ROOT開始，如果ROOT中，包含有[Ki>K]，即ROOT中所有大于K的最小檢索鍵，且[Ki]是ROOT中所有的檢索鍵，查找路徑會轉向與[Ki]對應指向[Pi]的子樹，查找過程將在該子樹的根節點上繼續進行。如果ROOT中不包含所有的檢索鍵[Ki]，表明[Ki]大于ROOT中包含的所有檢索鍵。根據MB+樹型結構定義，遍歷查找過程將在該子樹的根節點上繼續進行。

在[Pod]或者幾指向的子樹根節點上繼續第一步驟的遍歷查找過程，并根據實際情況繼續向MB+樹的葉節點進行延伸[7]。

MB+算法查詢失效總代價[FsL]如下，

關鍵字數目[Ki]，葉節點[pi]，f為約束條件，m為設定參數。如果查詢過程已經延伸到葉節點，若葉節點中包含[Ki]=[K]，說明與[K]對應的數據文件塊存在;若葉節點中的所有[Ki]≠[K]，說明樹型結構中不存在被查詢的數據文件塊。本文優化的MB+樹查詢算法的程序（部分）如下，

設不能立即確定某個記錄在MB+樹中找到，則需繼續在數據塊中查找。本次優化算法查找可分為順序查找和插入查找，MB+樹中順序查找，是按照從鏈頭開始，順著整個數據鏈，對數據庫文件順序處理;如果是要求從某一節點或者樹根開始，則需要從對應的某個記錄層起始。就是使用隨機的查找方法，從中間節點或者樹根開始，查找到要求的數據記錄。再按照順序查找的方法，從這一記錄開始順序查找其它記錄。如果在算法中，為插入的節點尋找插入地址，運用二分法在每一層節點找到插入的位置，保證在該節點插入后，該MB+樹仍保持原有有序性[8]。進行窗口查詢時，在MB+樹上可以有效地進行過濾，各中間節點中的child節點按其順序排列就是其關鍵之處。正是因為有序性使得基于MB+這種結構的查詢速度很快。

2 實驗

2.1 驗證MB+樹節點訪問效率

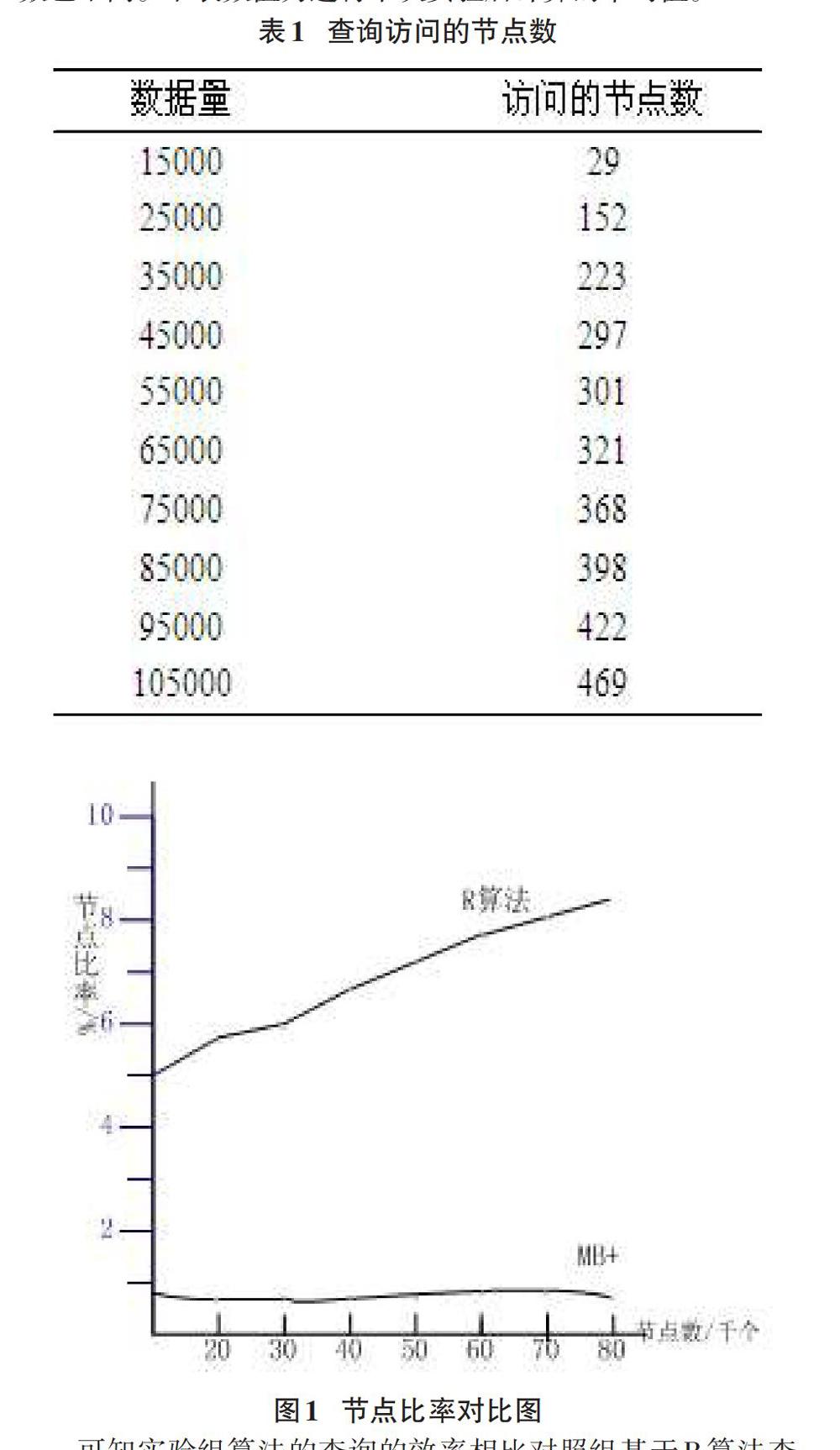
實驗是在Windows 8 系統， Inter i7中央處理處理器 4GHz，8GB RAM硬件平臺上，用c++ 程序語言實現的，由計算機隨機產生實驗數據。以傳統R樹為基礎的數據庫查詢算法為對照組，優化的MB+算法為實驗組。隨機產生數據，生成 MB+樹中 M= 20， P1（10，30），P2（40，110），方向查詢向量（1，0.5）。通過計算機隨機產生實驗數據，該算法訪問對應的數據時，統計經過的節點數而得到實驗結果， MB+樹的中間隔值參數為 50。由上文優化流程可知，即使每次訪問的數據相同，但是根據MB+樹本身特性可知，由于數據儲存的不同分布，會使得訪問節點數也不同。下表數值為進行十次實驗后計算的平均值。

2.2 MB+樹查詢消耗比較

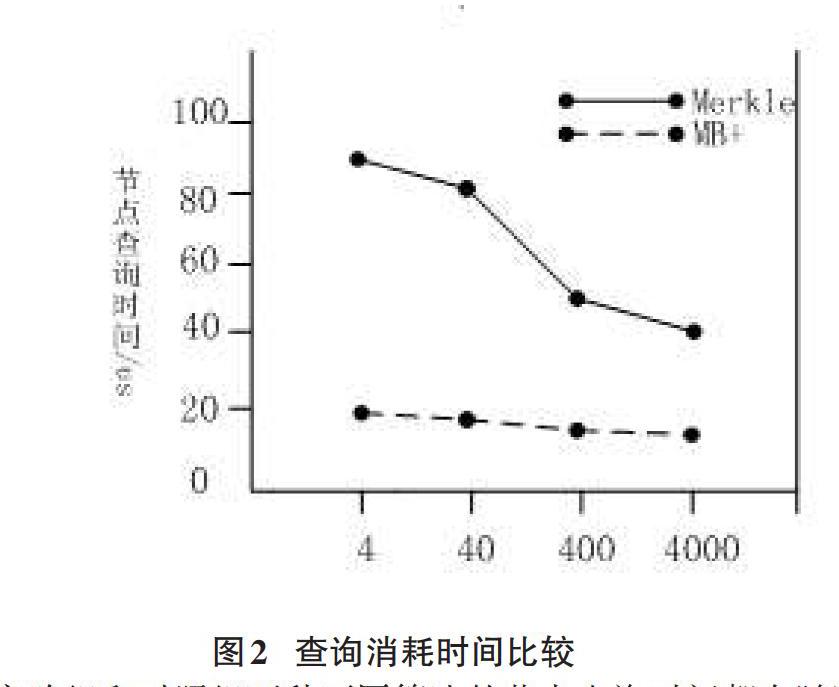
從節點的查詢檢驗時間來考察，本文基于MB+樹的數據庫查詢優化算法為實驗組，傳統的Merkle散列樹查詢算法為對照組，計算機隨機生成數據組，對節點查詢時間進行比較。結果如下圖所示：

實驗組和對照組兩種不同算法的節點查詢時間都在隨數據項增加而減少，并且下減幅度都逐漸趨于穩定但是基于MB+樹的查詢算法消耗明顯少于基于Merkle散列樹的查詢算法。

3 結語

大數據的發展將不同產業、領域、行業的信息整合到一起，構成完整數據庫。互聯網的不斷發展，對數據庫的查詢算法的要求越來越高。快速、準確、消耗小的查詢算法是未來的發展趨勢。本次優化的基于MB+樹的數據庫查詢算法，從查詢節點、查詢消耗等方面，相比傳統算法有所提升。而且優化后的算法無論在理論步驟簡化的層面上，還是對比實驗的效果上都要優于之前的數據庫查詢算法，可以進行推廣。

參考文獻：

[1] 李凌， 張蕾， 楊洋，等. 一種基于MB+樹的網絡共享數據查詢和檢驗方法[J]. 計算機應用研究， 2018， 35（3）： 782-787.

[2] 施恩， 顧大權， 馮徑等. B+樹索引機制的研究及優化[J]. 計算機應用研究， 2017， 34（6）： 1766-1769.

[3] 高潔. 基于改進和聲搜索群算法的數據庫查詢優化[J]. 現代電子技術， 2017， 40（3）： 114-116.

[4] 鄧小鴻， 劉惠文. 基于四叉樹分解和MB_LBP模式的人臉識別算法[J]. 電視技術， 2017（Z3）.

[5] 丁建立， 羅云生， 王家亮，等. 基于B+樹的發布/訂閱并行匹配算法[J]. 計算機工程與設計， 2018（1）： 66-71.

[6] 陳晉音， 施晉， 杜文耀，等. 基于MB-RRT～*的無人機航跡規劃算法研究[J]. 計算機科學， 2017， 44（8）： 198-206.

[7] 王科俊， 曹逸， 邢向磊. 基于MB-CSLBP的指靜脈加密算法研究[J]. 智能系統學報， 2018 （4）： 55-61.

[8] 岑瑤， 潘新， 郜曉晶，等. 基于MB-LBP和HOG的掌紋識別[J]. 計算機應用研究， 2017， 34（3）： 920-923.

【通聯編輯：張薇】